Vecteurs dans l'espace Comment graphiquement, applications, exercices

UN vecteur dans l'espace Tout est représenté par un système de coordonnées donné par X, et et z. Presque toujours l'avion Xy C'est le plan de la surface horizontale et de l'axe z représente la hauteur (ou la profondeur).

Les axes de coordonnées cartésiennes illustrés à la figure 1, divisez l'espace en 8 régions appelées Octaveuse, analogue à la façon dont les axes X - et Divisez l'avion en 4 quadrants. Nous aurons alors 1 octant, 2e Oanto et ainsi de suite.

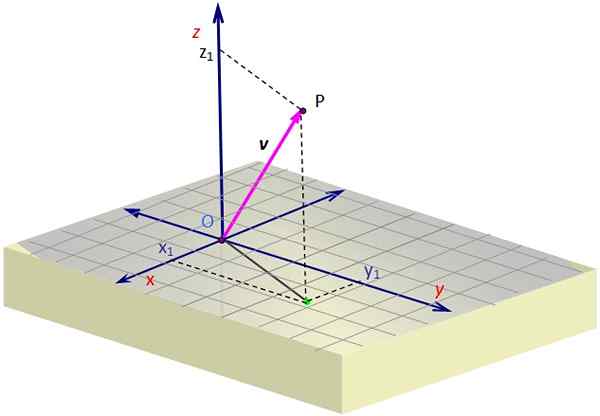
Figure 1. Un vecteur dans l'espace. Source: auto-faite.

La figure 1 contient une représentation d'un vecteur V dans l'espace. Une certaine perspective est nécessaire pour créer l'illusion de trois dimensions sur le plan de l'écran, qui est réalisée en dessinant une vue oblique.

Pour représenter un vecteur 3D, vous devez aider les lignes pointillées qui déterminent les coordonnées de la projection ou de "l'ombre" de la grille V À la surface x et et. Cette projection commence en o et se termine au point vert.

Une fois là-bas, vous devez continuer par la verticale à la hauteur (ou à la profondeur) nécessaire en fonction de la valeur de z, Jusqu'à ce que vous arriviez à p. Le vecteur est tiré de O et se terminant par P, qui dans l'exemple est dans le 1er ocant.

[TOC]

Applications

Les vecteurs dans l'espace sont largement utilisés en mécanique et autres branches de physique et d'ingénierie, car les structures qui nous entourent nécessitent une géométrie dans les trois dimensions.

Les vecteurs de position dans l'espace sont utilisés pour positionner des objets par rapport à un point de référence appelé Origine SOIT. Ce sont donc également des outils nécessaires en navigation, mais ce n'est pas tout.

Peut vous servir: vagues électromagnétiques: théorie Maxwell, types, caractéristiques

Les forces agissant sur des structures telles que les boulons, les supports, les câbles, les entretoises et plus sont la nature vectorielle et sont orientés dans l'espace. Pour connaître son effet, il est nécessaire de connaître votre adresse (et aussi votre point de candidature).

Et souvent la direction d'une force est connue de deux points dans l'espace qui appartiennent à sa ligne d'action. De cette façon, la force est:

F = F ou

Où f est l'ampleur ou le module de force et ou Il s'agit du vecteur unitaire (module 1) dirigé le long de la ligne d'action de F. 

Notation et représentations vectorielles 3D

Avant de résoudre quelques exemples, la notation des vecteurs 3D sera brièvement examinée.

Dans l'exemple de la figure 1, le vecteur V, dont le point d'origine coïncide avec l'origine ou et dont la fin est le point P, a des coordonnées X et z positif, tout en coordonnée et C'est négatif. Ces coordonnées sont: X₁, et₁, z₁, qui sont précisément les coordonnées de p.

Donc, si nous avons un vecteur lié à l'origine, c'est-à-dire dont le point de départ coïncide avec O, il est très facile d'indiquer ses coordonnées, qui seront celles du point extrême ou P. Pour faire la distinction entre un point et un vecteur, nous utiliserons pour les dernières lettres et supports audacieux, comme ceci:

V = < x₁, et₁, z₁ >

Tandis que le point P est indiqué par des parenthèses:

P = (x₁, et₁, z₁)

Une autre représentation utilise des vecteurs unitaires Toi, J et k qui définissent les trois directions de l'espace dans les axes X, et et z respectivement.

Ces vecteurs sont perpendiculaires les uns aux autres et constituent un Base ortonormale (Voir figure 2). Cela signifie qu'un vecteur 3D peut être écrit en termes d'eux comme:

Peut vous servir: mouvement ondulé: caractéristiques, types de vagues, exemples

V = V_X Toi + V_et J + V_z k

Angles et directeurs de cosenos d'un vecteur

La figure 2 montre également les angles des réalisateurs γ₁, γ₂ et γ₃ que le vecteur V respectivement avec les axes X, et et z. Connaissant ces angles et l'ampleur du vecteur, cela est complètement déterminé. De plus, les cosinus des réalisateurs remplissent la relation suivante:

(cos γ₁)² + (cos γ₂)² + (cos γ₃)² = 1

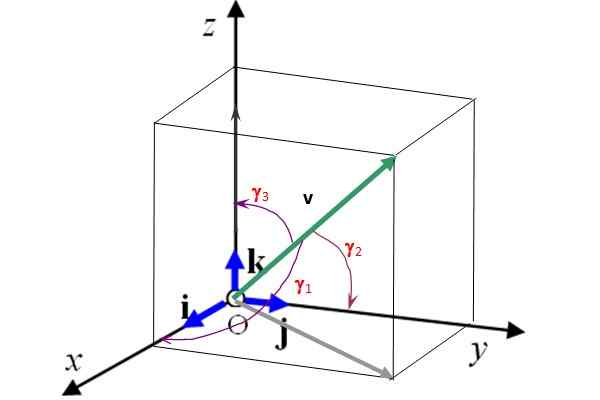Figure 2. Les vecteurs unitaires I, J et K déterminent les 3 directions préférentielles de l'espace. Source: auto-faite.

Exercices résolus

-Exercice 1

Dans la figure 2, les angles γ₁, γ₂ et γ₃ que le vecteur V du module 50 forme avec les axes de coordonnées sont respectivement: 75.0º, 60.0º et 34.3e. Trouvez les composants cartésiens de ce vecteur et représentez-le en termes de vecteurs unitaires Toi, J et k.

Solution

La projection du vecteur V sur l'axe X c'est v_X = 50 . Cos 75º = 12.941. De même, la projection de V sur l'axe et c'est v_et = 50 cos 60 º = 25 et enfin sur l'axe z c'est v_z = 50. COS 34.3e = 41.3. Maintenant V peut être exprimé comme:

V = 12.9 Toi + 25.0 J + 41.3 k

-Exercice 2 

Trouvez des tensions dans chacun des câbles qui maintiennent le seau de la figure qui est en équilibre, si le poids est de 30 n.

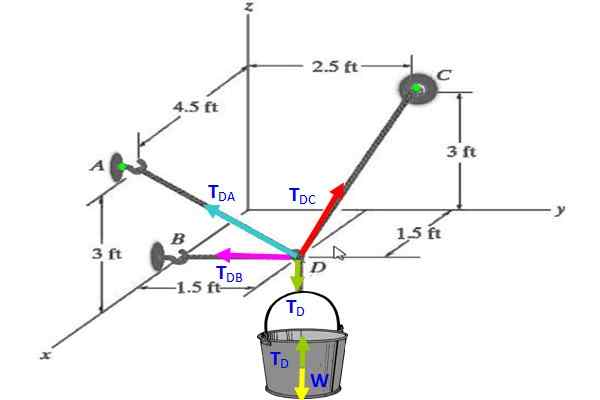figure 3. Diagramme des tensions pour l'exercice 2.

Solution

Sur le seau, le diagramme du corps libre indique que T_D (vert) compense le poids W (jaune), donc t_D = W = 30 n.

Dans le nœud, le vecteur T_D  Il est dirigé verticalement en bas, alors:

T_D = 30 (-k) N.

Pour établir les tensions restantes, vous devez suivre les étapes suivantes:

Étape 1: Trouvez les coordonnées de tous les points

A = (4.5; 0; 3) (A est sur le plan mural X-Z)

B = (1.5; 0; 0) (B est sur l'axe x)

Peut vous servir: adresse (physique)

C = (0, 2.5, 3) (C est sur le plan mural et Z)

D = (1.5; 1.5; 0) (D est sur le plan horizontal  x et et)

Étape 2: Trouvez les vecteurs dans chaque direction en soustrayant les coordonnées de la fin et du début

Donner =

Dc =

Db =

Étape 3: Calculer les modules et les vecteurs unitaires

Un vecteur unitaire est obtenu par expression: ou = r / r, avec r (en gras) étant le vecteur et r (sans gras) le module dudit vecteur.

Da = (3² + (-1.5)² + 3²)^½ = 4.5; Dc = ((-1.5) ² + 1² + 3²)^½ = 3.5

ou_Donner = 4.5 =

ou_Dc = 3.5 =

ou_Db =

ou_D =

Étape 4: Exprimez toutes les tensions en tant que vecteurs

T_Donner = T_Donner ou_Donner = T_Donner

T_Dc = T_Dc ou_{Dc =}  T_Dc

T_Db = T_Db ou_Db = T_Db

 T_D = 30

Étape 5: Appliquez la condition d'équilibre statique et résolvez le système d'équations

Enfin, la condition de bilan statique est appliquée au seau, de sorte que la somme vectorielle de toutes les forces sur le nœud est vide:

T_Donner + T_Dc + T_Db + T_D = 0

Comme les tensions sont dans l'espace, cela conduira à un système à trois équations pour chaque composant (X, et et z) de tensions.

0.67 t_Donner -0.43 t_Dc + 0 t_Db = 0

-0.33 T_Donner + 0.29 T_Dc - T_Db = 0

0.67 t_Donner + 0.86 t_Dc +0 t_Db - 30 = 0

La solution est: t_Donner = 14.9 N; T_Donner = 23.3 N; T_Db = 1.82 N

Les références

1. Bedford, 2000. POUR. Mécanique pour l'ingénierie: statique. Addison Wesley. 38-52.
2. Figueroa, D. Série: Physique pour la science et l'ingénierie. Volume 1. Cinématique.31-68.
3. Physique. Module 8: vecteurs. Récupéré de: Frtl.UTN.Édu.ardente
4. Hibbeler, R. 2006. Mécanique pour les ingénieurs. Statique. 6e édition. Société de rédaction continentale. 15-53.
5. Vector de calculatrice d'ajout. Récupéré de: 1728.org