Calcul du vecteur d'équilibreur, exemples, exercices

Il vecteur d'équilibrage C'est celui qui contraste le vecteur résultant et il est donc capable d'équilibrer un système, car il a la même ampleur et la même direction, mais contrairement à cela.

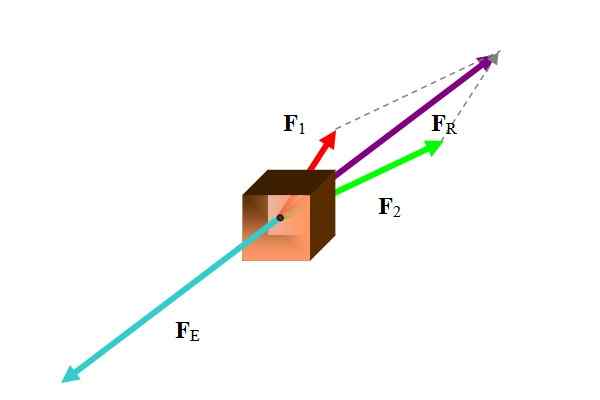
À de nombreuses reprises, le vecteur d'équilibrage fait référence à un vecteur de force. Pour calculer la force d'équilibrage, la force résultante est d'abord, comme le montre la figure suivante:

Figure 1. Sur un corps, deux forces agissent dont le résultat est équilibré par la force en couleur turquoise. Source: auto-faite.

Il existe différentes méthodes pour entreprendre cette tâche, selon les données à portée de main. Comme les forces sont des vecteurs, le résultat est la somme vectorielle des forces participantes:

F_R = F₁ + F₂ + F₃ +  .. .

Parmi les méthodes à utiliser figurent des méthodes graphiques telles que des méthodes polygonales, parallélogrammées et analytiques telles que la décomposition des forces dans leurs composants cartésiens. Dans l'exemple, la figure a été utilisée la méthode de parallélogramme.

Une fois la force résultante trouvée, la force d'équilibrage est précisément le vecteur opposé.

Ouais F_ET C'est la force d'équilibrage, alors il est accompli que F_ET Appliqué à un certain point, il garantit l'équilibre de la traduction du système. S'il s'agit d'une seule particule, il ne bougera pas (ou peut-être qu'il le fait à une vitesse constante), mais s'il s'agit d'un objet étendu, il aura toujours la possibilité de tourner:

F_R + F_ET = 0

[TOC]

Exemples

Les forces d'équilibrage sont présentes de tous les côtés. Nous sommes nous-mêmes équilibrés par la force que la chaise exerce pour compenser le poids. Les objets trouvés au repos: les livres, les meubles, les plafonds et un grand nombre de mécanismes sont en continu en cours d'équilibre par des forces.

Peut vous servir: chocs inélastiques: dans une dimension et des exemples

Par exemple, un livre de repos sur une table est équilibré par la force normale qu'elle exerce sur le livre, l'empêchant de tomber. Il en va de même pour la chaîne ou le câble qui maintient la lampe qui pend au plafond dans une pièce. Les câbles qui tiennent une charge sont répartis leur poids par la tension en eux.

Dans un fluide, certains objets sont capables de flotter et de rester au repos, car leur poids est équilibré par une force ascendante exercée par le liquide, appelé pousser.

Divers mécanismes doivent être équilibrés en connaissant le vecteur de force d'équilibrage tel que les barres, les poutres et les colonnes.

Lorsque vous utilisez un équilibre, il est nécessaire d'équilibrer en quelque sorte le poids de l'objet avec une force équivalente, soit en ajoutant des poids ou par ressorts.

Table des forces

Le tableau des forces est utilisé en laboratoire pour déterminer la force équilibrée. Il se compose d'une plate-forme circulaire, dont vous avez la vue supérieure sur la figure, et qui a un transporteur pour mesurer les angles.

Aux bords de la table, il y a des poulies à travers lesquelles des cordes qui maintiennent des poids et qui convergent dans un cerceau qui se trouve au centre.

Par exemple, deux poids sont suspendus. Les tensions générées sur les cordes par ces poids sont dessinées en rouge et bleu sur la figure 2. Un tiers pèse le vert, peut équilibrer la force résultante des deux autres et garder le système en équilibre.

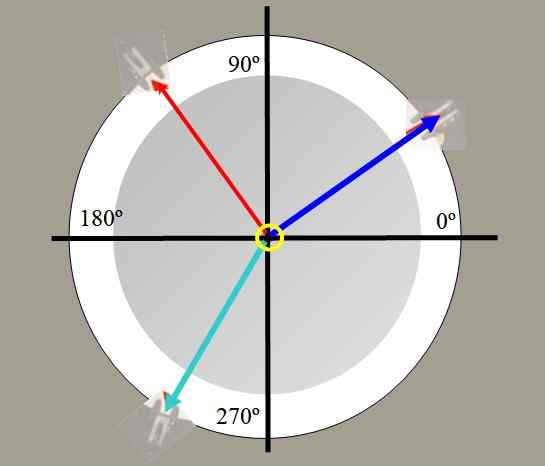Figure 2. Vue du haut du tableau des forces. Source: auto-faite.

Avec la table des forces, vous pouvez vérifier le caractère vecteur des forces, décomposer les forces, trouver la force d'équilibrage et vérifier le théorème de Lamy:

Peut vous servir: soleil

Si un Le corps est en équilibre grâce à trois forces coplanaires, simultanées et non colinéaires (non parallèles), appelées POUR, B et C, La relation entre ces forces est la suivante:

A / sin α = b / sen β = c / sen γ

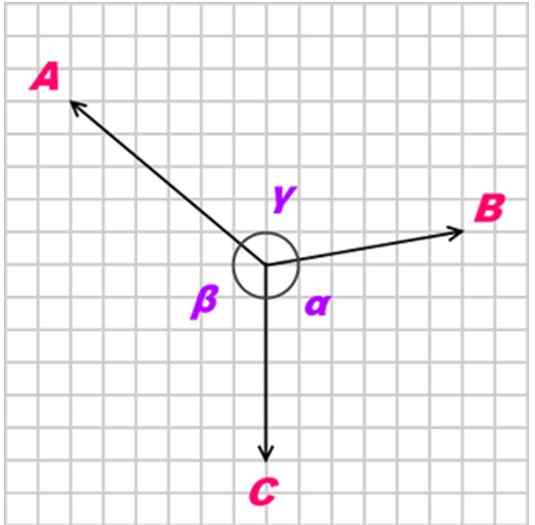figure 3. Le théorème de Lamy s'applique aux forces simultanées et coplanaires. Source: Wikimedia Commons.

Exercices résolus

-Exercice 1

Dans le tableau des forces de la figure 2, les pèvres de 225 g (tension bleue) et 150 g (tension rouge) sont pendues, avec les angles illustrés. Trouvez la valeur de la force d'équilibrage et l'angle que cette forme avec l'axe vertical.

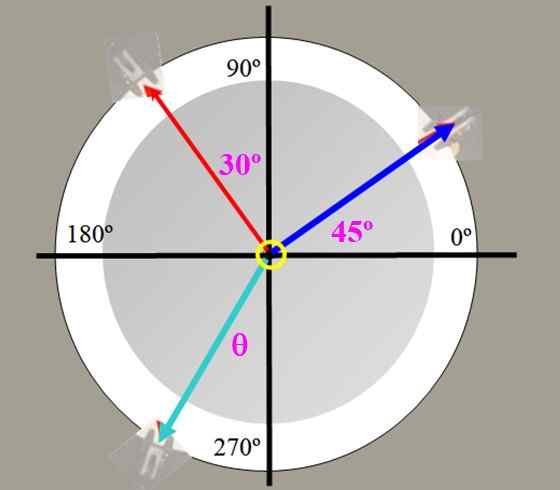Figure 4. Table des forces pour l'exercice 1.

Solution

Le problème peut être résolu avec les poids exprimés en grammes (forces). Laisser p₁ = 150 grammes et P₂ = 225 grammes, les composants respectifs de chacun sont:

P_{1 fois} = 225 . cos 45º g = 159.10 g; P_1Y = 225 . cos 45º g = 159.10 g

P_2x = -150 . Sen 30º g = -75.00 g; P_{2 et} = 150 . Cos 30º g = 129.90 g

Le poids qui en résulte P_R Les composants ajoutent algébriquement:

P_Rx = 159.10 - 75.00 g = 84.10 g

P_Ry = 159.10 + 129.90 g = 289.00 g

Le poids d'équilibrage P_ET est le vecteur opposé P_R:

P_Ex = -84.10 g

P_Hé = -289.00 g

L'ampleur du poids d'équilibrage est calculée par:

P_ET = (P_Ex² + P_Hé²)^1/2 = (-84.dix)² + (-289.00)²)^1/2 G = 301 g

L'angle θ de la figure est:

θ = arctg (-84.10 / -289.00) = 16.2e par rapport à l'axe et négatif.

-Exercice 2

Trouvez le vecteur d'équilibrage du système illustré sur la figure, sachant que chaque carré mesure 10 m côté.

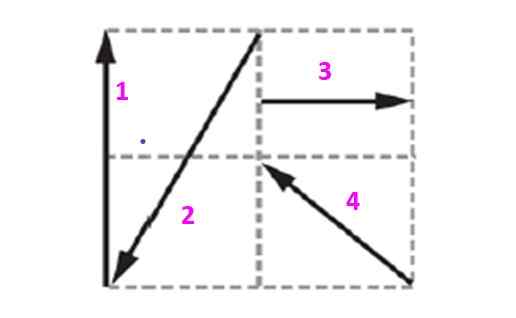Figure 5. Diagramme pour l'exemple résolu 2.

Solution

Les vecteurs contenus dans cette grille seront exprimés en termes d'unité et de vecteurs orthogonaux Toi et J qui déterminent l'avion. Vecteur 1, qui sera désigné comme V₁ Il a une amplitude de 20 m et est dirigé verticalement vers le haut. Il peut être exprimé comme:

Il peut vous servir: transfert de chaleur par rayonnement (avec des exemples)

V₁ = 0 Toi +vingt J m

D'après le dessin, il est observé que le vecteur 2 est:

V₂ = -10 Toi - vingt J m

Le vecteur 3 est horizontal et pointe dans l'adresse positive:

V₃ = 10 Toi + 0 J  m

Enfin, le vecteur 4 est incliné 45 º, car il est la diagonale du carré, donc ses composants mesurent le même:

V₄ = -10 Toi + dix J m

Notez que le signe -.

Le vecteur résultant est obtenu en ajoutant la composante du composant:

V_R = -10 Toi + dix J m

Ensuite, le vecteur d'équilibrage du système est:

V_ET = 10 Toi - dix J m

Les références

1. Beardon, t. 2011. Une introduction aux vecteurs. Récupéré de: nrich.Mathématiques.org.
2. Bedford, 2000. POUR. Mécanique pour l'ingénierie: statique. Addison Wesley. 38-52.
3. Figueroa, D. Série: Physique pour la science et l'ingénierie. Volume 1. Cinématique.31-68.
4. Physique. Module 8: vecteurs. Récupéré de: Frtl.UTN.Édu.ardente
5. Hibbeler, R. 2006. Mécanique pour les ingénieurs. Statique. 6e édition. Société de rédaction continentale. 15-53.
6. Vector de calculatrice d'ajout. Récupéré de: 1728.org
7. Vecteurs. Récupéré de: wikibooks.org