Variable ordinale

Qu'est-ce qu'une variable ordinale?

Une variable ordinale est celle qui prend des valeurs qui peuvent être commandées (ou désigner une commande). Par exemple, la variable de stature d'une personne peut être classée comme: élevée, moyenne et faible.

Une échelle ordinale, en plus d'identifier, de regrouper et de différencier les unités d'étude, en tant que variable nominale, décrit également l'ampleur et, par conséquent, est caractérisée par l'ordre; c'est-à-dire que les unités d'étude peuvent être commandées de plus en plus ou de plus en plus en termes d'ampleur.

Cette échelle parle du premier, du deuxième, du troisième ou du haut, moyen, basse; Mais la mesure n'est pas établie entre les classes. Par exemple: la qualification variable dans un test de satisfaction pour un service fourni, peut être mesurée en quatre catégories: insatisfait, indifférent, satisfait, très satisfait.

Il peut être commandé en fonction de la satisfaction manifeste, mais on ne sait pas à quel point.

L'échelle ordinale fait référence à des mesures qui ne font que des comparaisons "majeures", "mineures" ou "égales" entre les mesures consécutives. Représente une classification ou une commande d'un ensemble de valeurs observées.

Concept de la variable ordinale et des caractéristiques

Sur une échelle ordinale, les observations sont placées dans un ordre relatif en ce qui concerne la caractéristique qui est évaluée. C'est-à-dire que les catégories de données sont classées ou commandées en fonction de la caractéristique spéciale qu'ils ont.

Si nous utilisons des nombres, l'ampleur de ceux-ci représente l'ordre de la plage de l'attribut observé. Seules les relations "supérieures à", "inférieures" et "égales à" ont un sens sur une échelle de mesure ordinale.

Peut vous servir: géométrie euclidienne

Du point de vue mathématique, et comme les échelles nominales, les échelles ordinales n'admettent que le calcul des proportions, des pourcentages et des raisons.

La mesure de tendance centrale qui explique le mieux une variable ordinale est la médiane, qui est la valeur située au centre de l'ensemble des données ordonnées du moins au plus grand.

Lorsque les objets sont classés par une caractéristique, il est possible d'établir quel objet a plus ou moins de la caractéristique par rapport à un autre; Mais la différence ne peut pas être quantifiée.

Par exemple, trois objets qui ont été ordonnés comme «d'abord», «deuxième» et «troisième», en tenant compte de toute caractéristique. La deuxième place diffère du premier d'une quantité qui n'est pas nécessairement égale à la quantité dans laquelle il diffère de la troisième place.

Exemples de variables ordinales

Quelques exemples de variables ordinales:

- Classe sociale (A - High; B - High Media; C - Media; D - Low; E - très bas).

- Notes d'école qualitative (I - insuffisante; a - acceptable; b - bon; s - exceptionnel; e - excellent).

- Diplômes militaires (général, colonel, lieutenant-colonel, major, capitaine, etc.).

- Degré de scolarité (primaire, lycée, technicien professionnel, technologue, université, etc.).

- Étape de développement d'un être humain (nouveau-né, bébé, enfant, jeune, adulte, vieux).

- Classification des films (A - Tous les publics; B - plus de 12 ans; C - plus de 18 ans; D - plus de 21 ans).

- Maturité d'un fruit (vert, peinture, mûr, très mature, pourri).

- Degré de satisfaction à l'égard de la fourniture d'une fonction publique. (Très satisfait; satisfait; indifférent; etc.).

Peut vous servir: données non groupées: exemples et exercice résolus

- Exemples expliqués

Évaluation d'un enseignant par ses élèves

Les étudiants d'un certain cours ont la possibilité de répondre à une enquête pour l'évaluation de la capacité pédagogique de leur enseignant, qui est mesurée avec une variable ordinale dont l'échelle est: 5 - Excellent, 4 - Eh bien, 3 - Moyenne, 2 - Bad, 1 - pauvre.

Les valeurs de la variable sont commandées de plus ou de mieux à moins ou de pire: excellent est mieux que bon, eh bien c'est mieux que la moyenne, etc. Cependant, il n'est pas possible de distinguer l'ampleur des différences.

Est la différence entre excellent et bon? Il n'est pas possible de l'affirmer.

Si nous utilisons les nombres, ceux-ci n'indiquent pas l'amplitude. Par exemple, il ne faut pas conclure que la bonne qualification (qualification 4) est deux fois plus élevée que la mauvaise (qualification 2). On peut dire que la bonne qualification est meilleure que la mauvaise note, mais il ne peut pas être quantifié dans quelle mesure il est mieux.

Niveau d'acceptation d'un repas

Un concours de dégustation évalue les repas dans un concours de cuisine à travers la variable ordinale au niveau d'acceptation exprimée en: A - Excellent, B - eh bien, C - Pas acceptable. L'utilisation d'une mesure ordonnée du plus haut à la plus basse est mise en évidence, mais il n'est pas possible d'établir la différence entre les valeurs d'échelle.

Puisqu'il s'agit d'un concours, comment le gagnant est-il déterminé? Il semble que le plus approprié soit l'utilisation de la mode pour prendre la décision du gagnant du concours. Comprendre la mode comme le nom donné à la plus grande valeur (la plus fréquente) des dénombrements par niveau. Par exemple, 5 A, 14 B, 10 C ont été comptés; La mode est B, car c'est le niveau qui avait la plus grande opinion.

Peut vous servir: fonction logarithmique: propriétés, exemples, exercices

Différences avec la variable nominale

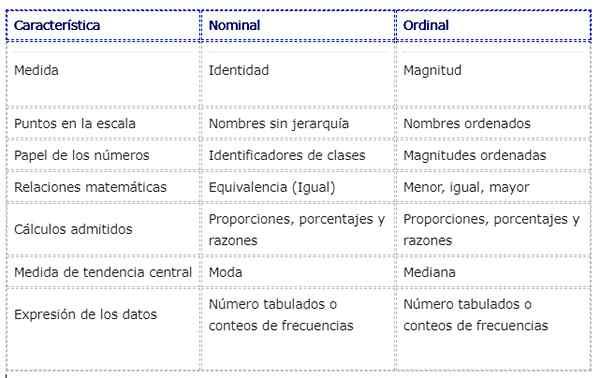
Le tableau suivant montre quelques différences et similitudes entre les variables mesurées à l'échelle nominale et ordinale:

Les références

1. Freund, R.; Wilson, W.; Mohr, D. (2010). Méthodes statistiques. Troisième Ed. Academic Press-Elsevier Inc.
2. Verre, g.; Stanley, J. (mille neuf cent quatre vingt seize). Méthodes statistiques non appliquées aux sciences sociales. Salle hispano-américaine S Hall S. POUR.
3. Jolie.; Marchal, W.; Wathen, s. (2012). Statistiques appliquées aux entreprises et à l'économie. Dixième ed. McGraw-Hill / Inter-American Editors S. POUR.
4. Orlandoni, G. (2010). Échelles de mesure statistique. Magazine Telos. Récupéré de OJS.ville.Édu.
5. Siegel, s.; Castellan, n. (1998). Statistiques non paramétriques appliquées aux sciences du comportement. Quatrième Ed. Trillas éditoriaux S. POUR.
6. Wikipédia. (2019). Niveau de mesure. Récupéré de.Wikipédia.org.