Méthode d'échantillonnage de quota, avantages, inconvénients, exemples

Il échantillonnage par quotas Il s'agit d'un moyen non provoque de prendre des données d'un échantillon d'attribution des frais par des strates. Les frais doivent être proportionnels à la fraction que représente cette couche en ce qui concerne la population totale et la somme des quotas doit être égale à la taille de l'échantillon. 

Le chercheur est celui qui décide de ce que seront les groupes ou les couches, par exemple, vous pouvez diviser une population en hommes et femmes. Un autre exemple de strates sont les gammes d'âge, par exemple de 18 à 25 ans, de 26 à 40 ans et à partir de 40.

Figure 1. Les frais d'échantillonnage sont segmentés en fonction des différences dans la population totale. Source: Pixabay.

Il est très pratique de savoir auparavant quel pourcentage de la population totale représente chaque strate. Ensuite, une taille d'échantillon est choisie qui est statistiquement significative, et des quotas proportionnels au pourcentage de chaque strate par rapport à la population totale sont attribués. La somme des frais par couche doit être égale à la taille totale de l'échantillon.

Enfin, les données des quotas attribuées à chaque strate sont prises, choisissant les premiers éléments qui complètent le quota.

C'est précisément à cause de cette façon non aliénante de choisir les éléments, que cette méthode d'échantillonnage est considérée comme non probabiliste.

[TOC]

Étapes pour effectuer l'échantillonnage des quotas

Étape 1

Segmenter la population totale de couches ou de groupes avec une caractéristique commune. Cette fonctionnalité sera précédemment décidée par le chercheur statistique que l'étude mène.

Étape 2

Déterminez quel pourcentage par rapport à la population totale représente chacune des strates ou des groupes choisis à l'étape précédente.

Étape 3

Estimer une taille d'échantillon statistiquement significative, selon les critères et les méthodologies de la science statistique.

Étape 4

Calculez le nombre d'éléments ou de quotas pour chaque strate, afin qu'ils soient proportionnels au pourcentage que chacun représente en ce qui concerne la population totale et la taille totale de l'échantillon.

Étape 5

Prenez les données des éléments dans chaque strate jusqu'à terminer le quota correspondant à chaque strate.

Cas pratique

Supposons que vous souhaitiez connaître le niveau de satisfaction concernant le service de métro dans une ville. Des études antérieures sur une population de 2000 personnes ont déterminé que 50% des utilisateurs jeunes Entre 16 et 21 ans, 40% sont Adultes entre 21 et 55 ans et seulement 10% des utilisateurs plus grand Plus de 55 ans.

Profiter des résultats de cette étude est segmenté ou stratifié en fonction de l'âge des utilisateurs:

-Jeunes: cinquante%

-Adultes: 40%

-Plus grand: dix%

Comme un budget limité est disponible, l'étude doit être appliquée à un petit échantillon, mais c'est statistiquement significatif. Une taille de 200 échantillon est choisie, c'est-à-dire que l'enquête au niveau de satisfaction sera appliquée à 200 personnes au total.

Peut vous servir: Sandwich Loi: Explication et exercices

Il est maintenant nécessaire de déterminer le quota ou le nombre d'enquêtes pour chaque segment ou strate, qui doit être proportionnel à la taille de l'échantillon et au pourcentage par strate. 

Quota de la strate

Le nombre d'enquêtes par strate est comme ceci:

Jeunes: 200 * 50% = 200 * (50/100) = 100 enquêtes

Adultes: 200 * 40% = 200 * (40/100) = 80 enquêtes

Plus grand: 200 * 10% = 200 * (10/100) = 20 enquêtes

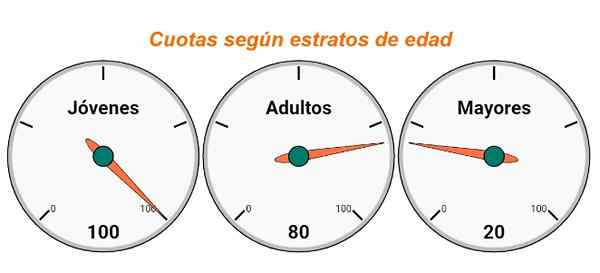Figure 2. Quotas dans un échantillon de 200 personnes selon l'âge de la strate. Source: F. Zapata.

Notez que la somme des frais doit être égale à la taille de l'échantillon, c'est-à-dire égal au nombre total d'enquêtes qui seront appliquées. Ensuite, les enquêtes sont transmises aux quotas pour chaque strate.

Il est important de noter que cette méthode est bien meilleure que de prendre toutes les enquêtes et de les transmettre aux 200 premières personnes qui apparaissent, car selon les données précédentes, il est très probable que la strate minoritaire soit en dehors de l'étude.

Applicabilité, avantages et inconvénients

Pour que la méthode soit applicable, un critère est requis pour la formation des strates, qui dépend de l'objectif de l'étude.

L'échantillonnage des quotas est adéquat lorsque vous souhaitez connaître les préférences, les différences ou les caractéristiques des secteurs pour diriger des campagnes spécifiques selon la strate ou le segment.

Son utilisation est également utile lorsque pour une raison quelconque, il est intéressant de connaître les caractéristiques ou les intérêts des secteurs minoritaires, ou lorsqu'ils ne veulent pas être exclus de l'étude.

Pour être applicable, le poids ou la signification de chaque strate doit être connu concernant la population totale. Il est très important que ces connaissances soient fiables, sinon de mauvais résultats seront obtenus.

avantage

-Les temps d'étude diminuent, car les quotas de strate sont généralement faibles

-Simplifie l'analyse des données.

-Minimise les coûts car l'étude s'applique aux petits mais bien des échantillons de représentation de la population totale.

Désavantages

-Comme les strates sont définies a priori, il est possible que certains secteurs de la population soient en dehors de l'étude.

-Lors de l'établissement d'un nombre limité de strates, il est possible que les détails de l'étude soient perdus.

-En évitant ou en incorporant dans le cadre d'un autre, une strate peut être mauvaise dans l'étude.

-Il est impossible d'estimer l'erreur d'échantillonnage maximale.

Application simple de l'application

Vous voulez faire une étude statistique sur le Niveau d'anxiété Dans une population de 2000 personnes. 

Le chercheur qui dirige des intuits de recherche que les différences dans les résultats doivent être trouvées en fonction de l'âge et du sexe. C'est pourquoi il décide de former trois couches d'âge indiquées comme suit: First_ead, Second_ad et Troisième âge. Concernant le segment sexe Les deux types habituels sont définis: Homme et Femme.

Peut vous servir: probabilité théorique: comment le sortir, exemples, exercices

Défini First_ead, Entre 18 et 25 ans, Second_ad celui entre 26 et 50 ans et enfin Troisième âge Entre 50 et 80 ans.

L'analyse des données de la population totale doit: 

45% de la population appartient au First_ead.

40% se trouve dans le Second_ad.

Enfin, seulement 15% de la population à l'étude appartient au Troisième âge.

En utilisant une méthodologie adéquate, qui n'est pas détaillée ici, il est déterminé qu'un échantillon de 300 personnes est statistiquement significatif.

Détermination des quotas par âge

L'étape suivante sera alors de trouver les quotas correspondants par le segment Âge, ce qui se fait comme suit:

First_eity: 300 * 45% = 300 * 45/100 = 135

Second_ad: 300 * 40% = 300 * 40/1 = 120

Tiers_ad: 300 * 15% = 300 * 15/100 = 45

Il est vérifié que la somme des quotas donne la taille totale de l'échantillon.

Détermination des quotas par âge et sexe

Jusqu'à présent, le segment n'a pas été pris en compte sexe De la population, deux couches ont déjà été définies à partir de ce segment: Femme et Homme. Encore une fois, vous devez analyser les données de la population totale, qui montrent les informations suivantes: 

-60% de la population totale est le sexe Femme.

-Pendant ce temps, 40% de la population à étudier appartient au sexe Homme.

Il est important de noter que les pourcentages précédents concernant la distribution de la population en fonction du sexe, ne prennent pas en compte l'âge. 

Étant donné qu'aucune information ne soit disponible, l'hypothèse sera faite que ces proportions en termes de sexe sont également distribuées dans les 3 couches de Âge qui ont été définis pour cette étude. Avec ces considérations, nous continuons maintenant à établir les quotas par âge et sexe, ce qui signifie qu'il y aura maintenant 6 sous-États:

S1 = premier_ad et femelle: 135 * 60% = 135 * 60/100 = 81

S2 = premier et homme: 135 * 40% = 135 * 40/100 = 54

S3 = seconde et femelle: 120 * 60% = 120 * 60/100 = 72

S4 = deuxième et homme: 120 * 40% = 120 * 40/100 = 48

S5 = troisième _tad et femelle: 45 * 60% = 45 * 60/100 = 27

S6 = troisième _dad et masculin: 45 * 40% = 45 * 40/100 = 18

Application enquête et étude des résultats

Une fois le segment des six (6).

Les enquêtes seront appliquées comme suit, 81 enquêtes sont prises et les 81 premières personnes dans le segment sont interrogées S1. Ensuite, cela se fait de la même manière avec les cinq segments restants.

Peut vous servir: quels sont les éléments d'un angle?

La séquence d'étude est la suivante:

-Analyser les résultats de l'enquête, qui sont ensuite discutées, analysant les résultats par segment.

-Faire des comparaisons entre les résultats du segment.

-Enfin élaborez des hypothèses qui expliquent les causes de ces résultats.

Différence avec l'échantillonnage aléatoire stratifié

Dans notre exemple dans lequel nous appliquons l'échantillonnage de quota, la première chose qui est faite est d'établir les frais puis de réaliser l'étude. Bien sûr, ces quotas ne sont pas entièrement capricieux, car ils ont été basés sur des informations statistiques antérieures sur la population totale.

Dans le cas de ne pas avoir d'informations préalables sur la population à l'étude, c'est une forme aléatoire préférable.

Une façon de s'assurer que le caractère aléatoire serait d'utiliser un générateur de nombres aléatoires et d'enquêter aux employés dont le nombre d'employés coïncide avec celui du générateur aléatoire.

Une fois que vous avez les données, et comme l'objectif de l'étude est de voir les niveaux d'anxiété en fonction de l'âge et des couches sexuelles, les données sont séparées en fonction des six catégories que nous avions précédemment définies. Mais sans établir de frais antérieurs.

C'est pour cette raison que la méthode de Échantillonnage aléatoire stratifié Il est considéré comme une méthode probabiliste. En attendant il échantillonnage par quotas Non précédemment établi non. 

Cependant, si les quotas sont établis avec des informations sur la base des statistiques de la population, alors on peut dire que la méthode de échantillonnage par quotas C'est approximativement probabiliste.

Exercice proposé

L'exercice suivant est proposé:

Dans un collège d'enseignement secondaire, une enquête sur la préférence entre étudier les sciences ou étudier les sciences humaines. 

Supposons que l'école compte un total de 1000 élèves regroupés à cinq niveaux selon l'année d'études. On sait qu'il y a 350 étudiants en première année, 300 en deuxième, 200 en troisième, 100 en quatrième et enfin 50 en cinquième année. Il est également connu que 55% des élèves sont des garçons et 45% sont des filles.

Déterminez les strates et les frais par la strate, pour connaître le nombre d'enquêtes pour s'appliquer à la participation aux segments de l'étude et du sexe. Supposons en outre que l'échantillon sera de 10% de la population totale d'étudiants.

Les références

1. Berenson, M. 1985.Statistiques pour l'administration et l'économie, les concepts et les applications. Éditorial inter-américain.
2. Statistiques. Échantillonnage par quotas. Récupéré de: EncyclopediaEconoma.com.
3. Statistiques. Échantillonnage. Récupéré de: statistiques.Tapis.Uson.mx.
4. Explorable. Échantillonnage par quotas. Récupéré de: explorable.com.
5. Moore, D. 2005. Statistiques de base appliquées. 2e. Édition.
6. Netquest. Échantillonnage probabiliste: échantillonnage stratifié. Récupéré de: NetQuest.com.
7. Wikipédia. Échantillon statistique. Récupéré de: dans.Wikipédia.org