Définition des vecteurs non-copplanaires, conditions, exercices

Les Vecteurs non-copplanares Ce sont ceux qui ne partagent pas le même plan. Deux vecteurs libres et un point définissent un seul plan. Un troisième vecteur peut ou non partager cet avion et si ce n'est pas le cas, ce sont des vecteurs non copplanaires.

Les vecteurs non couplés ne peuvent pas être représentés dans des espaces à deux dimensions tels qu'une planche ou une feuille de papier, car certains d'entre eux sont contenus dans la troisième dimension. Pour les représenter correctement, vous devez utiliser la perspective.

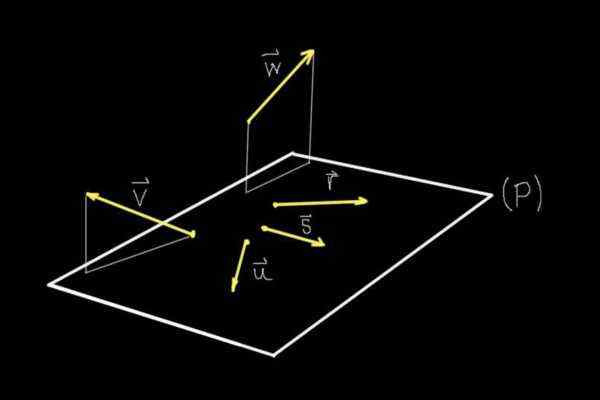Figure 1. Coplanares et vecteurs de couplage. (Élaboration propre)

Si nous observons la figure 1, tous les objets strictement montrés sont dans le plan de l'écran, mais grâce à la perspective, notre cerveau est capable d'imaginer un avion (P) qui sort du même.

Sur ce plan (P) se trouvent les vecteurs r, s, ou, Alors que les vecteurs V et W  Ils ne sont pas sur cet avion.

Par conséquent, les vecteurs r, s, ou Ce sont des coplanarios ou des coplanares les uns avec les autres car ils partagent le même plan (P). Les vecteurs V et W Ils ne partagent aucun appartement avec aucun des autres vecteurs indiqués, donc ils ne sont pas à couplage. 

[TOC]

Coplanares et vecteurs d'équations planes

Un avion est défini de manière unique si trois points sont donnés dans l'espace à trois dimensions.

Supposons que ces trois points soient le point POUR, le point B Et le point C qui définit l'avion (P). Avec ces points, il est possible de construire deux vecteurs AB = U et AC = V qui sont par construction avec l'avion (P).

Le produit vectoriel (ou produit transversal) de ces deux vecteurs entraîne un troisième vecteur perpendiculaire (ou normal) et donc perpendiculaire au plan (P):

n = u X V   => n ⊥ ou  et n ⊥ V   => n ⊥ (P)    

Peut vous servir: poids (physique): calcul, unités, exemples, exercices

Tout autre point qui appartient à l'avion (P) doit accomplir que le vecteur Aq être perpendiculaire au vecteur n; Cela équivaut à dire que le produit scalaire (ou le produit ponctuel) n avec Aq Il doit être nul:

n • Aq = 0 (*)

La condition précédente équivaut à dire que:

Aq • (ou X V) = 0 

Cette équation garantit que le point Q appartenir à l'avion (P). 

Équation cartésienne de l'avion

L'équation précédente peut être écrite de manière cartésienne. Pour cela, nous écrivons les coordonnées des points POUR, Q et les composants du vecteur normal n:

A = (a, b, c)

Q = (x, y, z)

n= (NX, NY, NZ)

De sorte que les composants AQ sont:

Aq= (X-a, y-b, z-c)

La condition pour le vecteur Aq être contenu dans l'avion (P) C'est la condition (*) qui est maintenant écrite comme ceci:

(NX, NY, NZ) • (X-A, Y-B, Z-C) = 0

Le calcul du produit ponctuel reste:

nx (x-a) + ny (y-b) + nz (z-b) = 0

S'il se développe et réorganise, il reste:

nx x + ny y + nz z = nx a + ny b + nz c

L'expression précédente est l'équation cartésienne d'un plan (P), en fonction des composants d'un vecteur normal pour (P) et les coordonnées d'un point POUR qui appartient à (P).

Les conditions pour que trois vecteurs soient non-Clanares

Comme la condition a été observée dans la section précédente Aq • (ou X V) = 0 garantit que le vecteur Aq C'est coplanario a ou et V.

Si nous appelons W au vecteur Aq Ensuite, nous pouvons affirmer cela:

W, ou et V Ce sont des coplanares, oui et seulement si W • ( ou X V ) = 0.

Condition de non-comportement

Si le produit triple (ou produit mixte) de trois vecteurs est différent de zéro, ces trois vecteurs ne sont pas de covers.

Il peut vous servir: processus politique: caractéristiques, applications et exemples

Ouais    W • ( ou X V ) ≠ 0 alors les vecteurs U, V et W sont des non-couplanarios.

Si les composants cartésiens des U, V, V et W sont introduits, l'état de non-comportement peut être écrit comme suit:

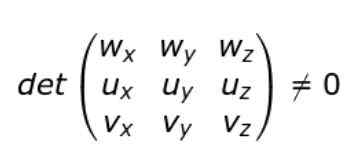C'est-à-dire que si le déterminant de la matrice (3 × 3) dont les lignes sont les composants des vecteurs U, V et W est alors les vecteurs ne sont pas.

Le produit triple a une interprétation géométrique et représente le volume du parallélépipé généré par les trois vecteurs non-CLANARES.

Figure 2. Trois vecteurs non couplage définissent un parallélépipedo dont le volume est le module de produit triple. (Élaboration propre)

La raison en est la suivante; Lorsque deux des vecteurs non couplage se multiplient. 

Ensuite, lorsque ce vecteur est multiplié. 

En d'autres termes, vous avez la zone de parallélogramme générée par les deux premiers multipliés par la hauteur du troisième vecteur.

Condition alternative de non-couplage

Si vous avez trois vecteurs et que l'un d'eux ne peut pas être écrit comme une combinaison linéaire des deux autres, alors les trois vecteurs ne sont pas de covers. C'est trois vecteurs ou, V et W Ce ne sont pas de covers si la condition:

α ou + β V + γ W = 0

Il n'est rempli que lorsque α = 0, β = 0 et γ = 0.

Exercices résolus

-Exercice 1

Vous avez trois vecteurs

ou = (-3, -6, 2);   V = (4, 1, 0) et W = (-1, 2, z)

Notez que le composant Z du vecteur W C'est inconnu.

Trouvez la plage de valeurs que Z peut prendre afin qu'il soit garanti que les trois vecteurs ne partagent pas le même plan.

Peut vous servir: équilibre stable: concept et exemples

Solution 

Nous appliquons à nouveau le critère du déterminant de la matrice formée par les rangs des trois vecteurs, de cette façon, nous restons: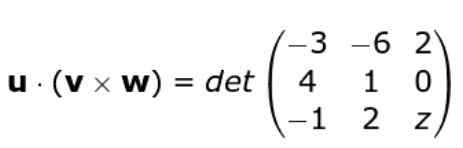Nous développons le déterminant

W • ( ou X V ) = -3 (z - 0) + 6 (4 z - 0) + 2 (8 + 1) = -3z + 24z + 18 = 21z + 18

Nous correspondons à cette expression à une valeur zéro

21 z + 18 = 0

Et nous effacons Z

Z = -18/21 = -6/7

Si la variable Z prenait la valeur -6/7, alors les trois vecteurs seraient des coplanares.

De sorte que les valeurs de z qui garantissent que les vecteurs sont des non-coverses sont celles qui sont dans l'intervalle suivant:

Z ∈ (-∞, -6/7) u (-6/7, ∞)

-Exercice 2

Trouvez le volume du paralléléprié illustré dans la figure suivante:

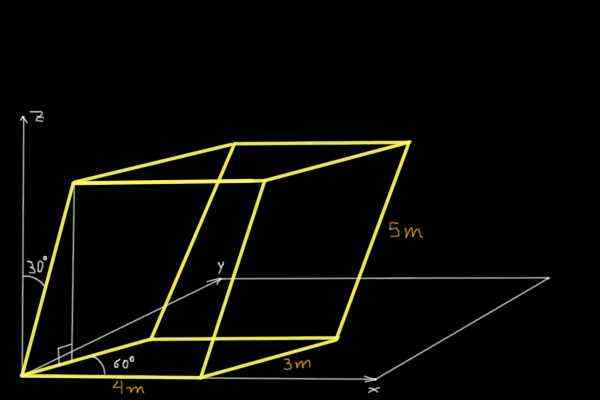
Solution 

Pour trouver le volume du parallèle illustré sur la figure, les composants cartésiens de trois vecteurs de couplage non concurrent seront déterminés à l'origine du système de coordonnées. Le premier est le vecteur ou  4m et parallèle à l'axe x:

ou= (4, 0, 0) m

Le second est le vecteur V Dans le plan de taille XY 3M qui forme 60º avec l'axe x:

V= (3 * cos 60º, 3 * Sen 60º, 0) = (1.5, 2.6, 0.0) M

Et le troisième le vecteur W de 5 m et dont la projection dans le plan XY forme 60º avec l'axe x, en plus w form 30º avec l'axe z.

W= (5 * sin 30º * cos 60º, 5 * Sen 30º * sin 60º, 5 * Sen 30º)

Effectué les calculs que nous avons: W= (1.25, 2.17, 2.5m.

Les références

1. Figueroa, D. Série: Physique pour la science et l'ingénierie. Volume 1. Cinématique. 31-68.
2. Physique. Module 8: vecteurs. Récupéré de: Frtl.UTN.Édu.ardente
3. Hibbeler, R. 2006. Mécanique pour les ingénieurs. Statique. 6e édition. Société de rédaction continentale.28-66.
4. McLean, W. Série Schaum. Mécanique pour les ingénieurs: statique et dynamique. 3e édition. McGraw Hill. 1-15.
5. Wikipédia. Vecteur. Récupéré de: c'est.Wikipédia.org