Caractéristiques de valeur actuelle, formules et exemples

Il valeur actuelle (VA) est la valeur actuelle d'un montant futur de l'argent ou des flux de trésorerie, en tenant compte d'un taux de rentabilité spécifique, à partir du moment de l'évaluation. En comptabilité, c'est le concept d'indicateur afin que les actifs et les passifs soient mesurés à la valeur actuelle à laquelle ils pourraient être vendus ou liquidés à la date actuelle.

Les montants futurs doivent faire face aux pressions inflationnistes ou déflationnaires, avec des coûts d'opportunité et d'autres risques qui affectent la valeur du montant final. La valeur équivalente réelle d'un montant à l'avenir ne sera pas le même montant qu'une somme d'argent aujourd'hui. C'est là que la valeur actuelle entre en jeu.

Source: Pixabay.com

Si vous avez une estimation de ce qui pourrait être gagné avec un investissement aujourd'hui, il peut être facilement estimé à quel point cette valeur future valait. Alternativement, la valeur actuelle indique également le montant qui serait nécessaire pour investir aujourd'hui si vous souhaitez terminer avec un montant mondial final, en supposant une certaine performance.

[TOC]

Caractéristiques

Un investisseur qui a de l'argent a deux options: le dépenser maintenant ou l'économiser. Compensation financière pour l'économiser et ne pas le dépenser, c'est que la valeur monétaire s'accumulera par l'intérêt composé que vous recevrez d'un emprunteur ou d'une banque.

Par conséquent, pour évaluer la valeur réelle d'une somme d'argent aujourd'hui après une certaine période de temps, les agents économiques combinent le montant d'argent à un certain taux d'intérêt.

Le fonctionnement de l'évaluation d'une valeur actuelle dans la valeur future est appelée capitalisation. Par exemple, combien vont le $ actuel en 5 ans?

L'opération inverse, qui évalue la valeur actuelle d'un montant futur, est appelé la remise. Par exemple, combien les 100 $ ont reçu en 5 ans, dans une loterie aujourd'hui?

Peut vous servir: Produits de substitution: caractéristiques et exemples

Valeur actuelle en comptabilité

La valeur actuelle est utile lorsqu'il y a eu une période prolongée d'inflation excessive. Dans ces conditions, les valeurs historiques dans lesquelles les actifs et les passifs ont été enregistrés seront probablement bien inférieurs à leurs valeurs actuelles.

Cependant, il n'y a pas de degré élevé d'acceptation du concept de valeur actuelle en comptabilité. Présente les problèmes suivants:

Coût comptable

Le temps est nécessaire pour accumuler des informations sur la valeur actuelle. Par conséquent, cela augmente le coût et le temps associés à la génération des états financiers.

Disponibilité des informations

Il peut être difficile ou impossible d'obtenir des informations sur la valeur actuelle sur certains actifs et passifs.

Précision de l'information

Certaines informations sur la valeur actuelle peuvent être moins basées sur des faits et plus sur des hypothèses ou des estimations mal fondées, affectant la fiabilité des états financiers lorsque ces informations sont incluses.

Formules

La valeur actuelle est une formule utilisée en finance qui calcule la valeur actuelle d'un montant qui sera reçu à une date future. La prémisse de l'équation est qu'il y a une "valeur d'argent au fil du temps".

La valeur de l'argent au fil du temps est le concept qui indique que recevoir aujourd'hui est plus que de recevoir ce même article à une date future.

La présomption est qu'il est préférable de recevoir 100 $ aujourd'hui que de recevoir le même montant d'argent dans un an à ce jour. Cependant, que se passe-t-il si les options étaient entre recevoir 100 $ dans le présent ou 106 $ en un an à partir d'aujourd'hui?

Une formule est nécessaire qui peut fournir une comparaison quantifiable entre un montant actuel et un montant à un moment futur, en termes de valeur actuelle.

Peut vous servir: Activités extractives: caractéristiques, types et exemples

Va = fn / (1 + r) ^ n, où

Fn = valeur future de la période n.

R = taux de retour ou rentabilité.

n = nombre de périodes.

Utilisation de la formule

La formule de la valeur actuelle a un large éventail d'utilisations. Par conséquent, il peut être appliqué à divers domaines des finances, notamment les finances des entreprises, la banque et l'investissement. Il est également utilisé comme composant d'autres formules financières.

Comment la valeur actuelle est-elle calculée?

Supposons que vous ayez actuellement 1000 $ et 10% d'intérêt annuel. Cela signifie que l'argent augmente de 10% chaque année, de telle manière:

1000 $ x (10% = 100) = 1100 $ x (10% = 110) = 1210 $ x (10% = 121) = 1331 $, etc.

-L'année prochaine, 1100 $ seront les mêmes que 1000 $ maintenant.

-En deux ans, 1210 $ seront les mêmes que 1000 $ maintenant.

-En trois ans, 1331 $ seront les mêmes que 1000 $ maintenant.

En fait, tous ces montants seront les mêmes dans le temps, considérant quand ils se produisent et avec 10% d'intérêt annuel.

Au lieu d'ajouter 10% chaque année, il est plus facile de se multiplier par 1,10. De cette façon, ce qui suit est obtenu: 1000 $ x 1,10 = 1100 $ x 1,10 = 1210 $ x 1,10 = 1331 $, etc.

Calculez la valeur future jusqu'à présent

Pour savoir quel argent à l'avenir en vaut actuellement la peine, il est calculé à l'envers, en divisant par 1,10 chaque année, au lieu de multiplier.

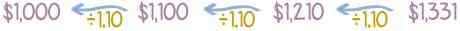
Par exemple, supposons qu'il est promis de payer 500 $ l'année prochaine. Le taux d'intérêt est de 10%. Pour savoir quelle est la valeur de ce montant aujourd'hui, la valeur future de 500 $ est divisée par 1,10, étant égale à 454,55 $ comme valeur actuelle.

Supposons maintenant qu'il est promis de payer 900 $ en trois ans. Pour connaître la valeur de ce montant aujourd'hui, ce montant futur est divisé par 1,10 trois fois. Ainsi, 900 $ en 3 ans seraient actuellement: 900 $ ÷ 1,10 ÷ 1,10 ÷ 1,10 = 900 $ ÷ (1,10 × 1,10 × 1,10) = 900 $ ÷ 1 331 = 676,18 $ maintenant.

Peut vous servir: rotation des stocks

Exemples

Exemple 1

Un individu veut déterminer combien d'argent devrait placer dans son compte de marché monétaire pour obtenir 100 $ en un an à ce jour, s'il gagne 5% d'intérêt dans son compte.

Les 100 $ que je voudrais recevoir en un an indique la partie F1 de la formule, 5% seraient R et le nombre de périodes serait simplement 1. En mettant cela dans la formule, il y aurait VA = 100 $ / 1,05 = 95,24 $. Aujourd'hui, je devrais déposer 95,24 $ pour obtenir 100 $ en un an, à un taux de 5%.

Exemple 2

Supposons qu'aujourd'hui un montant soit déposé dans un compte, qui gagne 5% d'intérêt par an. Si l'objectif est d'avoir 5 $.000 Dans le compte au bout de six ans, vous voulez savoir combien vous devez déposer dans le compte aujourd'hui. Pour cela, la formule de valeur actuelle est utilisée:

Valeur actuelle = valeur future / (1 + taux d'intérêt) ^ Nombre de périodes.

Insertion des informations connues, vous avez:

VA = 5 $.000 / (1 + 0,05) ^ 6 = 5 $.000 / (1 3401) = 3 $.731.

Les références

1. Steven Bragg (2018). Comptabilité de valeur actuelle. Outils comptables. Tiré de: Accountingools.com.
2. Formules financières (2019). Valeur actuelle. Tiré de: financeforulas.filet.
3. Mathsisfun (2019). Valeur actuelle (PV). Tiré de: Mathsisfun.com.
4. DQYDJ (2019). Calculatrice de valeur actuelle et explication de la formule de valeur actuelle. Pris de: dqydj.com.
5. Pamela Peterson (2019). Exemple de valeur actuelle. Université James Madison. Pris de: educ.JMU.Édu.
6. Wikipedia, The Free Encyclopedia (2019). Valeur actuelle. Pris de: dans.Wikipédia.org.