Valeur absolue

Quelle est la valeur absolue?

Il valeur absolue d'un nombre réel est défini comme la distance entre ce nombre et 0 de la ligne réelle. Pour être une distance, sa valeur est toujours positive ou nulle et égale à la figure du nombre.

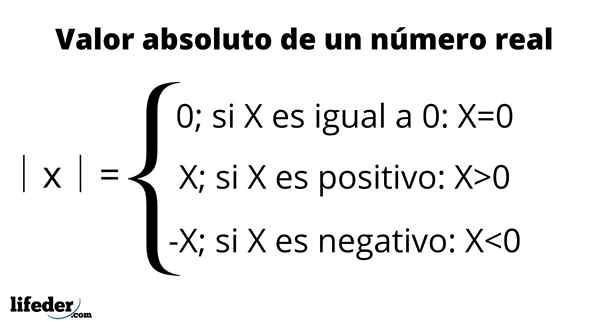
La valeur absolue est représentée en plaçant le nombre entre deux barres verticales, un symbole qui est lu: "valeur absolue de», Comme résumé dans le tableau suivant:

Par exemple, la valeur absolue de -3 est écrite en │ -3│ et est égale à 3. Cela signifie qu'entre -3 et 0, il y a trois unités, ce qui représente les nombres sur la ligne réelle. D'un autre côté, la valeur absolue de +3 ou simplement 3, est également égale à 3, car en mesurant sa distance à 0, il est également de trois unités.

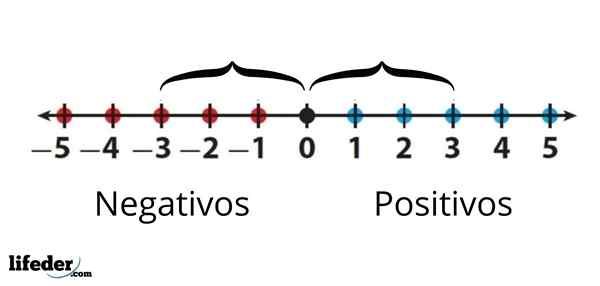La valeur absolue de -3 est égale à la valeur absolue de +3, car la distance entre soit à 0, c'est la même

En résumé, la valeur absolue d'un nombre est la même figure du nombre mais toujours avec un signe positif.

Propriétés de la valeur absolue

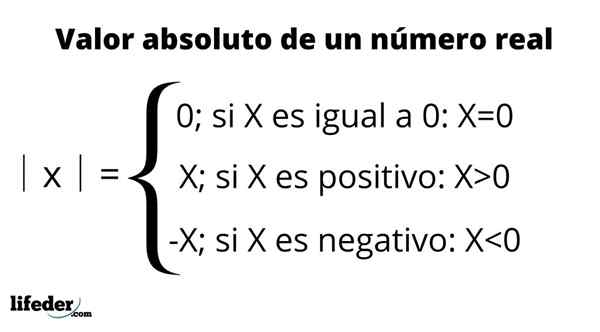Définition de la valeur absolue

Les principales propriétés de la valeur absolue:

• 1) La valeur absolue d'un nombre est toujours positive ou 0 donc:

│x│≥ 0

• 2) La valeur absolue de zéro est également nulle, c'est-à-dire │0│ = 0, il peut donc être affirmé que:

│x│ = 0, oui y seulement si x = 0

• 3) Pour chaque nombre x appartenant à l'ensemble des nombres réels, la valeur absolue de x est égale à la valeur absolue de - x:

│x│ = │ - x│

• 4) Si la valeur absolue d'un nombre x est a, cela signifie qu'il existe deux options pour ce nombre: i) x = + a ou ii) x = -a.

Il peut vous servir: Mary voyage 2/4 du cyclepist, Melissa Travels 4/8 et Anahi Travels 3/6

Par exemple, si la valeur absolue d'un nombre est de 5, les deux possibilités sont que le nombre est +5 ou -5.

Opérations avec une valeur absolue

Les propriétés suivantes sont très utiles pour effectuer des opérations avec des valeurs absolues:

• 5) Pour «x» et «y» qui sont deux nombres réels, l'inégalité suivante est toujours réalisée, appelée inégalité triangulaire de valeur absolue:

│x│ + │y│≥ │x + y│

Par exemple, soyez:

x = -6

y = 9

Le côté gauche de l'inégalité est:

│-6│ + │9│ = 6 + 9 = 16

Et le côté droit est:

│-6 + 9│ = │3│ = 3

De toute évidence, 16 est supérieur ou égal à 3, et c'est toujours le cas lorsque les nombres x et ont des signes différents. S'ils ont des signes égaux, alors l'égalité est obtenue. Voir cet autre exemple avec deux autres valeurs différentes:

x = -5

y = -3

│-5│ + │-3│≥ │-5-3│

5 + 3≥│-8│

En effet:

8 = 8

• 6) Le produit des valeurs absolues respectives de deux nombres réels "x" et "y" est égal à la valeur absolue du produit des nombres:

│x│ ∙ │y│ = │x ∙ y│

Sont encore les valeurs:

x = -6

y = 9

Ensuite:

│-6│ ∙ │9│ = 6 ∙ 9 = 54

Qui est égal à:

│ (-6) ∙ 9│ = │-54│ = 54

• 7) Le quotient de la valeur absolue de deux nombres réels "x" et "y", avec le dénominateur différent de 0, est la valeur absolue du quotient entre ces nombres:

Tant que et ≠ 0.

Exemple:

Exemples de valeur absolue

Exemples simples

Le calcul de la valeur absolue de tout nombre réel est très simple, par exemple la valeur absolue des nombres suivants est:

a) │-14│ = 14

b) │ - (- 5) │ = │5│ = 5

c) │π│ = π

Calculs avec la valeur absolue d'un nombre réel

Effectuez les opérations suivantes qui impliquent la valeur absolue:

a) 2⋅│8│ + 5⋅│ -16│-⋅│4│ = (2⋅8) + (5⋅16) - 4 = 16 + 80 - 4 = 92

b) │5- (8⋅3) │- 6 + │81 ÷ (-3) │ 

Peut vous servir: moitié de 15

Ceci est une opération combinée, il est donc préférable de le résoudre par étapes. La première valeur absolue est:

│5- (8⋅3) │ = │5-24│ = │-19│ = 19

La deuxième valeur absolue qui apparaît est calculée comme suit:

│81 ÷ (-3) │ = │-27│ = 27

Ensuite, les résultats obtenus sont recueillis et le calcul final est effectué:

│5- (8⋅3) │- 6 + │81 ÷ (-3) │ = 19- 6 + 27 = 40

La distance entre deux points sur la ligne réelle

La valeur absolue apparaît dans de nombreuses applications, comme trouver la distance entre deux nombres qui appartiennent à la ligne réelle. Si A est un nombre réel, il est situé sur la ligne réelle au point dont l'abscisse est «A», la même chose se produit avec un numéro réel B.

Laissez "A" et "B" deux nombres sur la ligne réelle, la distance qui les sépare est:

d_{UN B} = │b - a│

Qui peut également être calculé par:

d_{UN B} = │a - b│

Par exemple, la distance entre a = 5 et b = 12 est:

D = │5−12│ = │12−5│ = 7

De cette façon, la valeur absolue de la soustraction entre deux nombres réels est simplement la distance qui les sépare sur la ligne réelle.

Fonction de valeur absolue

La fonction de valeur absolue est une application qui va sur l'ensemble des nombres réels ℛ jusqu'à ℛ⁺, qui correspond à chaque nombre réel sa valeur absolue. Il est défini par:

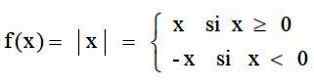
Et son graphique a la forme V typique:

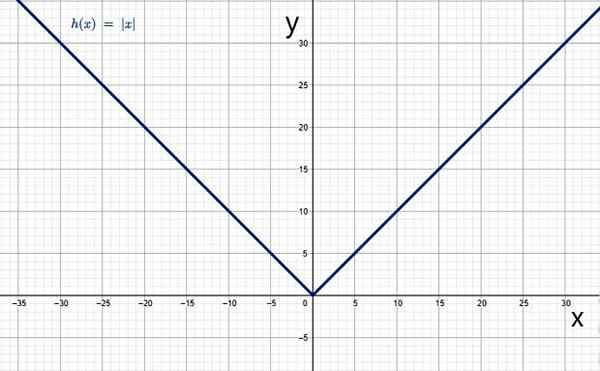La valeur absolue en fonction. Source: F. Zapata à travers Geogebra.

Caractéristiques de la fonction de valeur absolue

-Votre domaine est l'ensemble de tous les nombres réels.

-C'est continu.

-C'est même, car il est accompli que f (x) = f (-x), donc l'axe vertical est un axe de symétrie.

-La plage de la fonction de valeur absolue est l'ensemble de ceux réels positifs, y compris 0, car la fonction représente toujours une distance, et c'est toujours positif ou nul.

Peut vous servir: quelle est la directive? (Géométrie)

-C'est une fonction par sections ou par parties.

-Diminue dans l'intervalle (-∞, 0) et croît en (0, + ∞).

L'argument de valeur absolue peut également être une fonction quadratique ou autre, par exemple, elle peut être définie:

• f (x) = │x²-5x + 3│
• g (x) = │sen x│

La valeur absolue est responsable de devenir positif les images de l'argument qui ont un signe négatif.

Exercices résolus

Exercice 1

Évaluez les expressions algébriques suivantes avec une valeur absolue:

a) │2x - 5│ + │ --x + 1│ à x = 3

b) │ (x - 5) ÷ (x + 4) │ à x = −1

Solution à

│2⋅3−5│ + │ - 3 + 1│ = │6−5│ + │ - 2│ = │1│ + 2 = 3

Solution B

│ (−1−5) ÷ (−1 + 4) │ = │ (−6) ÷ (3) │ = │ - 2│ = 2

Exercice 2

Quel est l'ensemble des valeurs qui représentent l'inégalité suivante?

│x│≤ 3

Solution

L'inégalité représente tous les nombres réels dont la valeur absolue est inférieure ou égale à 3, donc c'est l'ensemble de tous les nombres entre -3 et +3, y compris ceux.

Dans la notation d'intervalle, il reste:

[-3,3]

Exercice 3

Résolvez l'équation suivante avec une valeur absolue:

│2x-1│ = 5

Solution 

Comme indiqué précédemment, pour résoudre une équation avec une valeur absolue, il est nécessaire de considérer les deux options. Je veux dire oui:

│f (x) │ = c

Ensuite:

1) f (x) = c

2) f (x) = -c

Par conséquent, cette équation, dont l'argument est linéaire, a deux solutions:

Première solution

2x - 1 = 5

2x = 6 ⇒ x₁ = 3

Deuxième solution

2x - 1 = -5

2x = -4 ⇒ x₂ = -2

Lors de l'évaluation de x₁ = 3 ou x₂ = -2 Dans l'équation d'origine, une égalité doit être obtenue, de cette manière, il est vérifié que les valeurs obtenues sont une solution de l'équation proposée. En effet:

│ (2⋅3) -1│ = │6-1│ = 5

Et lorsque vous essayez avec la deuxième option, une égalité est également obtenue:

│2⋅ (-2) -1│ = │-4-1│ = 5

Les références

1. Baldor, un. 2005. Algèbre. Groupe de patrie culturelle.
2. Larson, R. 2012. Précalation. 8e. Édition. Cengage Learning.
3. Hoffman, J. Sélection de problèmes de mathématiques. 2ieme volume.
4. Stewart, J. 2007. Précaulement: mathématiques pour le calcul. 5e. Édition. Cengage Learning.
5. Zill, D. 1984. Algèbre et trigonométrie. McGraw Hill.