Hendecagon

Qu'est-ce qu'un endecagon?

Il Hendecagon, aussi appelé Undecágono, C'est une figure géométrique plate avec 11 côtés qui appartiennent à la famille des polygones.

Ceux-ci sont nommés en fonction de la quantité de côtés qu'ils ont et dans le cas de l'Endecagon, leur nom dérive des mots grecs "Hendeka" et "Gona": Eleven et Vertex, respectivement, selon le fait que l'Endecagon a 11 sommets ou conseils.

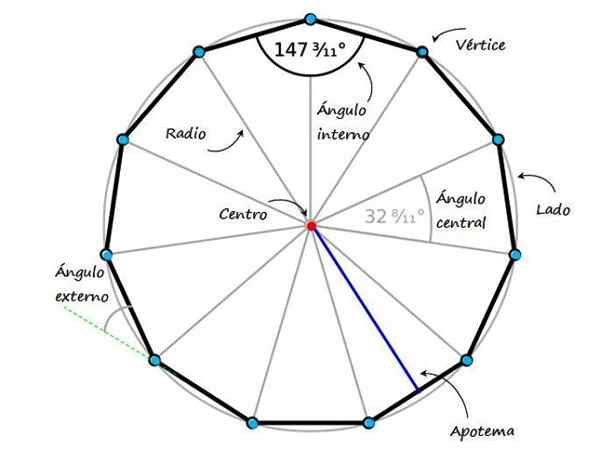
Figure 1. Un endecagon régulier et ses éléments. Source: F. Chaussure Wikimedia Commons modifiée.

Les polygones réguliers partagent une série de caractéristiques distinctives,. La figure 1 montre une endecagon régulière et ses propriétés les plus importantes:

• Côtés, Un total de 11.
• Sommets, Il y a également 11 points qui rejoignent deux côtés consécutifs (dans la figure précédente, les points bleus sont les points bleus et dans la figure 3, ils sont également nommés avec des majuscules).
• centre, point équidistant des sommets et des côtés.
• Diagonales, lignes qui rejoignent un sommet avec un autre sommet non consécutif, au total de 44.
• Angles internes, Ceux qui se forment entre deux côtés adjacents sur le côté interne de l'Endecagon. Si l'Endecagon est régulier, tous les angles internes mesurent 147 ^3/11 º.
• Angles externes, Ils sont formés entre un côté et l'allongement de l'un des côtés consécutifs.
• Radio, Distance du centre à un sommet.
• Angle central, que dans le cas de l'Endecagon régulier mesure 32 ^11/11 º, dont les côtés sont deux segments adjacents et le sommet de l'angle coïncide avec le centre.
• Apothème, segment perpendiculaire qui rejoint le centre d'un côté avec le centre de la figure.

Il peut vous servir: Hipparco de Nicea: biographie et contributions à la science

Comment faire un endecagon régulier?

Pour dessiner une endecagon ordinaire, dont les côtés mesurent la même chose, vous avez besoin d'une règle et d'une boussole. Une façon de faire la mise en page consiste à suivre ces étapes:

1.- Dessinez une circonférence et deux diamètres de celui-ci, un vertical et un autre horizontal. Les points de la circonférence déterminés par ces diamètres sont nommés et B (diamètre horizontal) et C et D (diamètre vertical).

2.- Ouvrez la boussole avec la mesure du rayon du cercle, soutenez la pointe au point D du diamètre du CD et dessinez un premier arc qui coupe la circonférence au point E.

3.- Avec cette même mesure, soutenez la pointe de la boussole au point A et dessinez une deuxième arche qui coupe la circonférence au point F et passe en même temps à travers le centre de la même.

4.- Ouvrez le rythme avec la pointe soutenue par E et au point F, dessinant un troisième arc qui coupe le diamètre vertical au point G.

5.- Maintenant, ouvrez la boussole entre les points F et G. Ce sera la mesure du côté endecagon. La pointe de la boussole est prise en charge en F et dessine un quatrième arc qui coupe la circonférence au point H, le côté FH appartient déjà à l'Endecagon et est dessiné en rejoignant les points à l'aide de la règle.

6.- La pointe de la boussole repose successivement au point H et sont soigneusement rédigées, joignant les points déterminés par des segments, jusqu'à onze côtés du polygone.

Exemples d'Endecágonos

Il existe plusieurs types d'endecargones, selon la mesure de leurs côtés et celle de leurs angles internes, en dessous de quelques exemples:

Endeconistes réguliers et irréguliers

-Régulier, Si tous les côtés et les angles internes mesurent le même.

Peut vous servir: numéro Euler ou numéro E: combien ok, propriétés, applications

-Irrégulier, Lorsque leurs côtés ont une mesure différente.

La figure suivante montre une endecagon régulière dans le contour interne d'un dollar américain avec la figure de Susan B. Anthony (1820-1906), militant des droits des femmes nés dans le Massachusetts, États-Unis. L'Endecagon a également été utilisé dans la conception d'autres pièces du monde.

Figure 2. Une endecagon ordinaire faisant partie du dollar Susan B Design. Anthony, inventé entre 1979 et 1981, puis lancé à nouveau en 1999. Source: Wikimedia Commons.

Convex et concaves endécargones

Les effectifs diffèrent en fonction de leurs angles internes, par exemple, ils peuvent être:

-Convexe, Si les angles internes sont inférieurs à 180º.

-Concave, Lorsqu'il y a des angles internes supérieurs à 180º.

L'endecagon qui décore le dollar Susan B. Anthony est convexe, car la mesure de l'un de ses angles internes est inférieur à 180 °. Sa valeur est calculée à travers une formule qui dépend du nombre de côtés sur la figure (voir la section suivante).

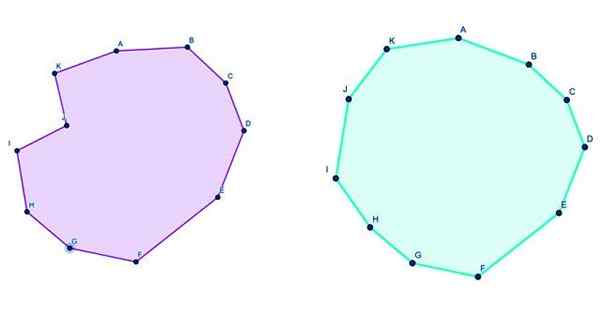figure 3. À gauche un endecagon convexe et à droite un endecagon concave. Source: F. Zapata à travers Geogebra.

Formules pour l'Endecagon

Formule pour les angles internes

Pour déterminer la mesure I en degrés, des angles internes de tout polygone régulier de n côtés, la formule suivante est utilisée:

 Le remplacement du nombre de côtés de l'Endecagon N = 11 dans la formule est obtenu:

 Et comme les angles internes de l'Endecagon ordinaire sont inférieurs à 180 °, cette figure est un polygone convexe.

La somme des angles internes d'un polygone ordinaire est trouvée par cette formule, valide pour entier et supérieur à 2:

Peut vous servir: angles dans la circonférence: types, propriétés, exercices résolus

S = (n - 2) x 180º

Remplacement n = 11 résultats:

S = (11 - 2) x 180º = 1620º

Angles externes

Pour connaître la mesure des angles internes, il est appliqué que la somme d'un angle interne et externe est égale à 180º:

180 º - 147 ^3/11º = 32 ^11/11º.

Périmètre

Le périmètre est la somme des côtés de l'Endecagon, que ce soit régulièrement ou non. Dans le cas de l'endecagon régulier, si ℓ C'est la longueur d'un côté, le périmètre se multiplie par n, La quantité de côtés.

Par conséquent, le périmètre P de l'Endecagon ordinaire est:

P = 11 ℓ

Zone

Connaissant le côté, la zone peut être calculée avec la formule:

Qui est approximativement:

A = 9.3656 ∙ ℓ²

Une autre façon de trouver la zone, à condition que l'Endecagon soit régulièrement, est de le diviser en triangles de base égaux au côté ℓ et de hauteur égale à la longueur de l'apothem l l_POUR.

La zone de chaque triangle est calculée par:

Zone = base x hauteur / 2

Cela selon apothem est également écrit comme:

Zone = ℓ. L_POUR / 2

Et la superficie totale de l'Endecagon multiplie la zone du triangle par 11:

A = 11ℓ. L_POUR / 2

En termes de périmètre, la zone d'Endecagon ordinaire est:

A = p. L_POUR / 2

Diagonales

Le nombre de diagonales est calculé en faisant n = 11 dans la formule suivante:

 D = [11 x (11-3)] / 2 = 44 diagonales.

Exercice résolu

Calculer le périmètre et la zone d'une endecagine régulière de 20 cm côté.

Solution

Le périmètre est:

P = 11 ℓ =11 × 20 cm = 220 cm.

Et sa zone est:

A = 9.3656 ∙ ℓ²= 9.3656 × (20 cm)²= 3746.2 cm²

Les références

1. Alexander, D. 2013. Géométrie. 5e. Édition. Cengage Learning.
2. Professeur de dessin. Endecágono inscrit dans une circonférence (polygone 11 côtés). Récupéré de: youtube.com.
3. Problèmes et équations. Calculateur de zone et de périmètre de l'Endecagon ordinaire. Récupéré de: Problèmes Syuses.com.
4. Mathématiques de Sangaku. Éléments d'un polygone et de sa classification. Récupéré de: Sangakoo.com.
5. Résolution de problèmes de géométrie automatique. L'endecagon. Récupéré de: Scuolaetrica.Article.
6. Wolfram Mathworld. Hendecagon. Récupéré de: Mathworld.Wolfram.com.