Nous expliquons ce que sont les mesures de dispersion, et nous donnons plusieurs exemples

Quelles sont les mesures de dispersion?

Le mesures de dispersion ou de variation, en statistiques, mesurez la distribution des données de la valeur d'une mesure centrale se déplace, comme la moyenne moyenne ou arithmétique. Sa valeur est toujours positive et normalement différente de 0, sauf dans le cas de données identiques.

Si une mesure de dispersion donne une petite valeur, cela signifie que les données sont situées très proches de la moyenne, mais si elle est importante, cela signifie que les données sont plus dispersées, par conséquent, loin de la moyenne.

Les mesures de dispersion sont très importantes du point de vue statistique, non seulement comme des indicateurs arithmétiques de la variation des données, mais comme une aide inestimable lorsque vous souhaitez améliorer la qualité, à la fois dans la fabrication de produits et dans la prestation de services.

Exemple de cela sont les rangs de l'attention dans les banques. Le temps moyen retardant les clients lorsqu'ils font une ligne unique, puis sont distribués au box-office, est le même que s'ils fabriquaient des lignes individuelles devant chaque.

Cependant, la dispersion est plus faible dans la ligne unique, ce qui signifie que le temps d'attention individuel est très similaire à chaque client. Les clients ont déclaré qu'ils se sentent plus à l'aise de cette manière, même si le temps de soins moyens est le même dans l'une ou l'autre des modalités.

Mesures de dispersion principale

Les principaux sont les suivants: le rang, la variance, l'écart type et le coefficient de variation.

Gamme

Le rang r d'un ensemble de données est défini à la différence entre la valeur maximale x_Max et la valeur minimale x_min dans le trou:

Rang = r = valeur maximale - valeur minimale = x_Max - X_min

Peut vous servir: quels sont les chiffres pour? Les 8 utilisations principales

La plage est rapide à calculer, mais elle est très sensible aux valeurs extrêmes et a l'inconvénient de ne pas prendre en compte les valeurs intermédiaires. Par conséquent, il est utilisé uniquement pour avoir une idée initiale, assez approximative de la dispersion des données.

Exemple de rang

Ceci est une liste du nombre d'ouragans dans l'Atlantique au cours des 14 dernières années:

8; 9; 7; 8; quinze; 9; 6; 5; 8; 4; 12 7; 8; 2

Les données de valeur maximale sont de 15 et la valeur minimale est par conséquent: par conséquent:

R = valeur maximale - valeur minimale = x_Max - X_min = 15 - 2 = 13 ouragans

Variance

Cette mesure est utilisée pour comparer chacune des données avec la moyenne de l'ensemble, et elle est calculée en ajoutant les différences, carrée élevée, entre chaque valeur avec la moyenne et la division par le nombre total de valeurs.

Être:

-La moyenne: μ

-Toute valeur, appartenant à l'ensemble de données: x_Toi

-Le nombre total d'observations: n

Indiquant la variance d'une population comme σ², L'expression pour le calculer est:

Et lorsqu'un échantillon d'une population est prélevé, il est préféré de calculer la variance de cette manière:

Où la variance de l'échantillon a été indiquée avec S, et la moyenne comme x avec barre, pour laisser l'utilisation de lettres grecques à la population. La raison de la division entre N-1, au lieu de n, est que la variance de l'échantillon ne sous-estime pas la population, ce qui se passe toujours lorsqu'il se divise entre n.

D'un autre côté, l'idée de carréage de chaque différence entre les données et la moyenne est de les empêcher de les ajouter 0, car certaines différences seront positives et d'autres négatives, ce qui a tendance à annuler la somme. Au lieu de cela, les carrés sont toujours positifs.

Il peut vous servir: Probabilité de fréquence: concept, comment il est calculé et des exemples

Par conséquent, la variance est toujours positive, même si la différence entre x_Toi Et la moyenne est négative, et son principal avantage de la variance est qu'il prend en compte chaque donnée de l'ensemble.

Mais il a la gêne de ses unités que ses unités ne sont pas les mêmes que celles des données, par exemple, si celles-ci sont consacrées à des temps, mesurées en quelques minutes, la variance de l'ensemble sera donnée en quelques minutes au carré.

Exemple de variance

Le calcul de la variance nécessite de trouver la moyenne. Prenant les données du nombre d'ouragan, la moyenne est calculée par:

(8 + 9 + 7+ 8 + 15 + 9 + 6 + 5+ 8 + 4 + 12 + 7 + 8+ 2) / 14 = 7.7 ouragans.Par conséquent, la variance est:

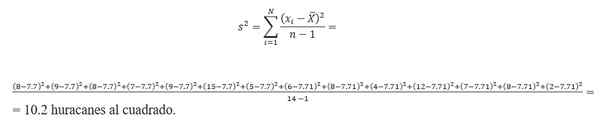
Écart-type

Pour corriger le problème du manque de concordance entre les unités, l'écart type est défini σ, Comme la racine carrée de la variance:

Et de manière analogue, dans le cas d'un échantillon:

Il existe une règle empirique pour estimer la valeur de l'écart type d'un échantillon de données, basé sur la plage. Selon cette règle, l'écart type est d'environ un quart de R:

S ≈ r / 4

Il a l'avantage de permettre une estimation rapide de l'écart type, car les opérations sont beaucoup plus simples.

L'écart type est, avec beaucoup, la mesure de dispersion la plus couramment utilisée, il vaut donc la peine de mettre en évidence ses principales caractéristiques:

• L'écart type indique combien les données médiatiques s'éloignent
• C'est toujours positif, mais cela peut être 0 si toutes les données sont identiques
• Plus la valeur de l'écart type est grande, plus les données sont dispersées
• Les unités d'écart type sont les mêmes que celles de la variable à l'étude
• Sa valeur change rapidement lorsque l'une des données (ou plusieurs) a une valeur très différente du reste
• Les valeurs d'écart type sont biaisées, c'est-à-dire que les moyennes de l'écart-type ne sont pas distribuées autour de la moyenne, contrairement à la variance, qui n'est pas biaisée.

Peut vous servir: triangle acutangle

Exemple d'écart type

Poursuivant avec l'exemple des ouragans, l'écart type est:

Ou, s'il est préféré utiliser l'approche de l'écart-type à travers la plage, une valeur assez proche est obtenue:

S = 13/4 = 3.25

Coefficient de variation

Le coefficient de variation est indiqué par les initiales CV ou R, dans certains textes, et à la fois pour une population, et pour un échantillon, relie l'écart standard et moyen, en pourcentage:

Ou bien:

Les équations sont valables tant que la moyenne est différente de 0.

En règle générale, le coefficient de variation est arrondi en une seule décimale et est utilisé pour comparer les données de deux populations différentes.

Exemple de coefficient de variation

Les temps d'attente en quelques secondes, pour les clients d'une banque, sont enregistrés dans deux situations: lorsqu'ils font une rangée unique et lorsqu'ils font des rangs individuels avant la billetterie d'attention. Les résultats sont les suivants:

Les deux ensembles de données peuvent être comparés grâce à leur coefficient de variation respectif:

Rangée unique

• Moyen = 429 secondes
• Déviation = 28.6 secondes
• Cv = (28.6/429) x 100 = 6.7 %

Rangs individuels

• Moyen = 429 secondes
• Déviation = 109.3 secondes
• CV = (109.3/429) x 100 = 25.5%

Comme cette dernière valeur est plus élevée, cela indique qu'il y a plus de variabilité dans les moments de service client lorsqu'ils font des rangs individuels que lorsqu'ils font une ligne unique, bien que le temps moyen soit le même dans chaque cas.