Propriétés, formules et équations d'Escaleno Trapezio

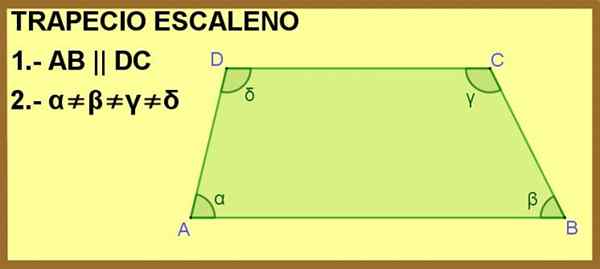
UN trapèze scalène Il s'agit d'un polygone à quatre faces, dont deux sont parallèles les uns aux autres, et avec ses quatre angles intérieurs de mesures différentes.

Le quadrilatère ABCD est montré, où les côtés AB et DC sont parallèles les uns aux autres. Avec cela, il suffit d'en faire un trapèze, mais en outre, les angles intérieurs α, β, γ et Δ sont tous différents, donc le trapèze est Escalano.

Figure 1. Le quadrilatère ABCD est un trapèze pour la condition 1 et le scalène pour la condition 2. Source: F. Zapata.

[TOC]

Éléments du scaleno trapectect

Sous les éléments les plus caractéristiques:

-Bases et côté: Les côtés parallèles du trapèzoïde sont ses bases et les deux côtés non parallèles sont les côtés.

Dans un trapèze scalène, les bases sont de différentes longueurs et les côtés aussi. Cependant, un trapèze scalène peut avoir un côté de longueur égale comme base.

-Médian: C'est le segment qui rejoint les points médians des côtés.

-Diagonale: La diagonale d'un trapèze est le segment qui rejoint deux sommets opposés. Un trapèze, comme chaque quadrilatoral, a deux diagonales. Dans le trapèze scalène, ils sont de longueur différente.

Autres trapézoïdes

En plus du trapèze d'escaleno, il existe d'autres trapézoïdes particuliers: le trapèzoïde rectangle et le trapézoïde isocèle.

Un trapèze est un rectangle lorsque l'un de ses angles est droit, tandis que le trapèze isocèle a ses côtés de longueur égale.

Le formulaire trapézoïdal a de nombreuses applications au niveau de la conception et de l'industrie, comme dans la configuration des ailes d'avion, la forme d'objets quotidiens tels que les tables, les sauvegardes de chaises, les conteneurs, les portefeuilles, les impressions textiles et plus encore.

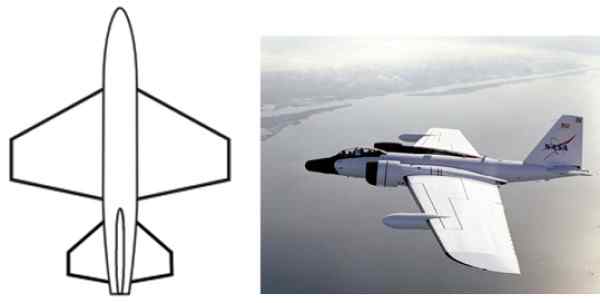Figure 2. La forme trapézoïdale est courante dans la configuration de l'avion alar. Source: Wikimedia Commons.

Propriétés

Ensuite, les propriétés du trapèze d'escalade sont répertoriées, dont beaucoup sont étendues aux autres types de trapézoïde. Dans ce qui suit, lorsque vous parlez de «trapèze», la propriété sera applicable à toute sorte, y compris le scalène.

1. La médiane du trapèzoïde, c'est-à-dire que le segment qui unit les points moyens de ses côtés non parallèles, est parallèle à l'une des bases.

2.- La médiane d'un trapèzoïde a une longueur qui est le semi-soum de ses bases et coupe ses diagonales au milieu.

3.- Les diagonales d'un trapèze se croisent à un point qui les divise en deux sections proportionnelles au rapport des bases.

4.- La somme des carrés des diagonales d'un trapèze est égale à la somme des carrés de ses côtés plus le double produit de ses bases.

5.- Le segment qui rejoint les points mi-diagonaux a une longueur égale à la semi-référence des bases.

Peut vous servir: fonction injective: de quoi elle consiste, à quoi sert-elle et des exemples

6.- Les angles adjacents aux côtés sont supplémentaires.

7.- Dans un trapèze scalène, la longueur de ses diagonales est différente.

8.- Un trapèze n'a une circonférence enregistrée que si la somme de ses bases est égale à la somme de ses côtés.

9.- Si un trapèze a une circonférence enregistrée, alors l'angle avec le sommet au centre de ladite circonférence et les côtés qui traversent les extrémités du latérale du trapèze est droit.

dix.- Un trapèze Escaleno n'a pas de circonférence circonscrite, le seul type de trapèze qui, s'il en est, est les isocèles.

Formules et équations

Les relations suivantes du trapèze d'escalade sont référées à la figure suivante.

1.- Si ae = ed et bf = fc → ef || AB et EF || Dc.

2.- Ef = (ab + dc) / 2 c'est: m = (a + c) / 2.

3.- Di = ib = d₁ / 2 et Ag = GC = D₂ / 2.

4.- Dj / jb = (c / a) de même CJ / JA = (c / a).

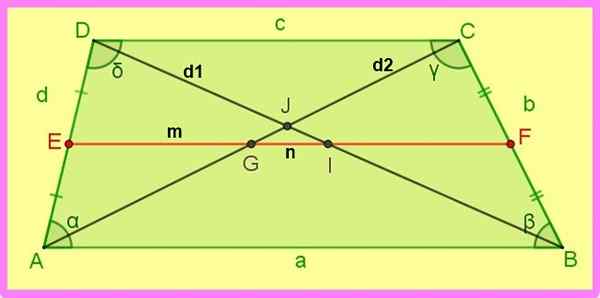figure 3. Médian et diagonales d'un trapèzoïde scalène. Source: F. Zapata.

5.- Db² + CA² = Annonce² + avant JC² + 2 AB ∙ DC 

Équivalence:

d₁² + d₂² = D² + b² + 2 a ∙ c

6.- Gi = (ab - dc) / 2

C'est-à-dire:

n = (a - c) / 2

7.- α + Δ = 180⁰ et β + γ = 180⁰

8.- Si α ≠ β ≠ γ ≠ δ alors d1 ≠ d2.

9.- La figure 4 montre un trapèze scalène qui a une circonférence enregistrée, dans ce cas, il est réalisé que:

A + c = d + b

dix.- Dans un trapèzoïde ABCD Escalène avec un centre enregistré du centre ou les éléments suivants est également rempli:

∡aod = ∡boc = 90⁰

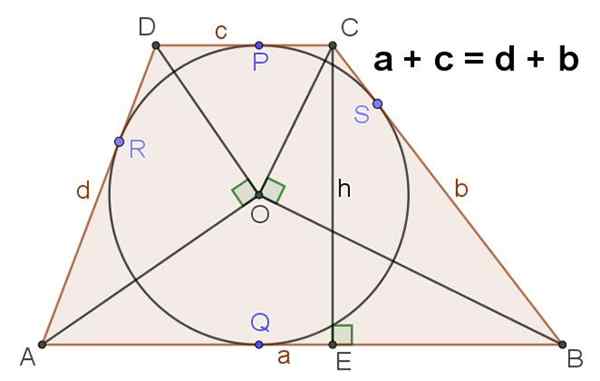Figure 4. Si dans un trapèze, il est vérifié que la somme de ses bases est égale à la somme des côtés, alors il y a la circonférence inscrite dans le même. Source: F. Zapata.

Hauteur

La hauteur d'un trapèze est définie comme le segment qui va d'un point de la base perpendiculairement à la base opposée (ou à son extension).

Toutes les hauteurs du trapèze ont la même mesure H, donc la plupart du temps, la hauteur du mot fait référence à sa mesure. En bref, la hauteur est la distance ou la séparation entre les bases.

La hauteur H peut être déterminée si la longueur d'un côté et l'un des angles adjacents au côté est connu:

H = d sin (α) = d sin (γ) = b sin (β) = b sin (δ)

Médian

La mesure médiane M du trapèze est les semi-bornes des bases:

M = (a + b) / 2

Diagonales

d₁ = √ [A² + d² - 2 ∙ a ∙ d ∙ cos (α)]

d₂= √ [A² + b² - 2 ∙ a ∙ b ∙ cos (β)]

Il peut également être calculé si seule la longueur du trapèze est connue:

d₁ = √ [b² + A ∙ c - a (b² - d²) / (a ​​- c)]

d₂ = √ [d² + A ∙ c - a (d² - b²) / (a ​​- c)]

Périmètre

Le périmètre est la longueur totale du contour, c'est-à-dire la somme de tous ses côtés:

Peut vous servir: variable aléatoire discrète

P = a + b + c + d

Zone

La zone d'un trapèzoïde est les semi-bornes de ses bases multipliées par sa hauteur:

A = h ∙ (a + b) / 2

Il peut également être calculé si la médiane M et la hauteur sont connues:

A = m ∙ h

Dans le cas où seule la longueur des côtés trapézoïdes est connue, la zone peut être déterminée par la formule d'Herón pour le trapèze:

A = [(a + c) / | a-c |] ∙ √ [(s-a) (s-c) (s-a-d) (s-a-b)]]]

Où s est le semi-périmètre: s = (a + b + c + d) / 2.

Autres relations pour l'escalade

La coupe de la médiane avec les diagonales et le parallèle qui passe par l'intersection des diagonales, donne naissance à d'autres relations.

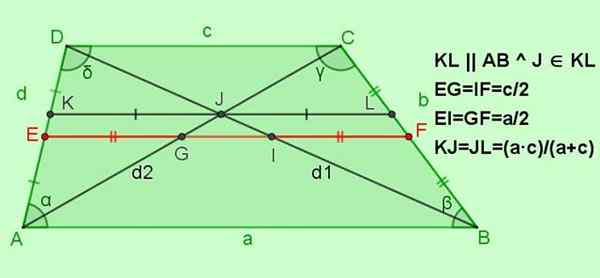Figure 5. Autres relations pour l'escalade. Source: F. Zapata.

-Relations pour EF médian

Ef = (a + c) / 2; Par exemple = if = c / 2; Ei = gf = a / 2

-Relations pour le segment parallèle avec les bases KL, et qui passe par le point de Intersection j des diagonales

Oui kl || Ab || Dc avec j ∈ Kl, alors kj = jl = (a ∙ c) / (a ​​+ c)

Construction du trapèze scalène avec règle et boussole

Compte tenu des bases de longueurs pour et c, étant un> c et avec le côté des longueurs b et d, être b> D, Nous procédons à ces étapes (voir figure 6):

1.- Avec la règle, le segment du plus grand AB est dessiné.

2.- À partir d'un SE et sur AB, le point P est marqué de sorte qu'AP = C.

3.- Avec la boussole avec C et Radio D Center, un arc est dessiné.

4.- Il est rendu au centre de B avec Radio B dessinant un arc qui interprète l'arc dessiné à l'étape précédente. Nous appelons ça le point d'intersection.

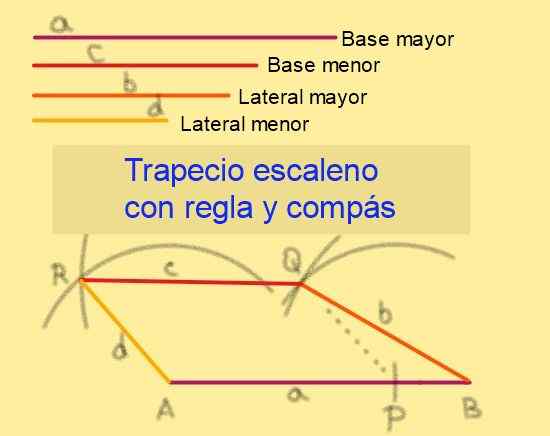Figure 6. Construction d'Escaleno Trapecio étant donné ses côtés. Source: F. Zapata.

5.- Avec centre pour dessiner un rayon arc d.

6.- Avec centre dans lequel dessiner un arc de rayon qui interceptait l'arc rédigé à l'étape précédente. Il sera appelé r au point de coupe.

7.- Les segments BQ, QR et RA sont dessinés avec la règle.

8.- Le quadrilatère ABQR est un trapézoïde scalène, car APQR est un parallélogramme, qui garantit que AB || QR.

Exemple

Les longueurs suivantes sont données en CM: 7, 3, 4 et 6.

a) Déterminez si vous pouvez construire un trapèze scalène qui peut circonscrire à une circonférence.

b) Trouvez le périmètre, la zone, la longueur des diagonales et la hauteur dudit trapèze, ainsi que le rayon de la circonférence enregistrée.

- Solution à

En utilisant les segments de longueur 7 et 3 comme bases et ceux de la longueur 4 et 6 comme côtés, un trapèzoïde scalène peut être construit en utilisant la procédure décrite dans la section précédente.

Nous devons vérifier s'il a une circonférence enregistrée, mais en nous souvenant de la propriété (9):

Peut vous servir: prisme hexagonal

Un trapèze n'a une circonférence enregistrée que si la somme de ses bases est égale à la somme de ses côtés.

Nous voyons cela en effet:

7 + 3 = 4 + 6 = 10

Alors l'état de la circonférence inscrite est rempli.

- Solution B

Périmètre

Le périmètre p est obtenu en ajoutant les côtés. Comme les bases totalisent 10 et les côtés aussi, le périmètre est:

P = 20 cm

Zone

Pour déterminer la zone, connu uniquement ses côtés, la relation est appliquée:

A = [(a + c) / | a-c |] ∙ √ [(s-a) (s-c) (s-a-d) (s-a-b)]]]

Où S est le semi-périmètre:

S = (A + B + C + D) / 2.

Dans notre cas, le semi-périmètre vaut S = 10 cm. Après avoir remplacé les valeurs respectives:

A = 7 cm; b = 6 cm; C = 3 cm; D = 4 cm

Est laissé:

A = [10/4] √ [(3) (7) (-1) (-3)] = (5/2) √63 = 19,84 cm².

Hauteur

La hauteur H est liée à la zone A à l'expression suivante:

A = (a + c) ∙ h / 2, où la hauteur peut être obtenue par autorisation:

H = 2a / (a ​​+ c) = 2 * 19,84 / 10 = 3 968 cm.

Radio de circonférence enregistrée

Le rayon de la circonférence enregistrée vaut la moitié de la hauteur:

R = h / 2 = 1 984 cm

Diagonales

Enfin, il y a la longueur des diagonales:

d₁ = √ [b² + A ∙ c - a (b² - d²) / (a ​​- c)]

d₂ = √ [d² + A ∙ c - a (d² - b²) / (a ​​- c)]

Le remplacement correcte des valeurs est:

d₁ = √ [6² + 7 ∙ 3 - 7 (6² - 4²) / (7 - 3)] = √ (36 + 21-7 (20) / 4) = √ (22)

d₂ = √ [4² + 7 ∙ 3 - 7 (4² - 6²) / (7-3)] = √ (16 + 21-7 (-20) / 4) = √ (72)

C'est-à-dire: D₁ = 4,69 cm et D₂ = 8,49 cm

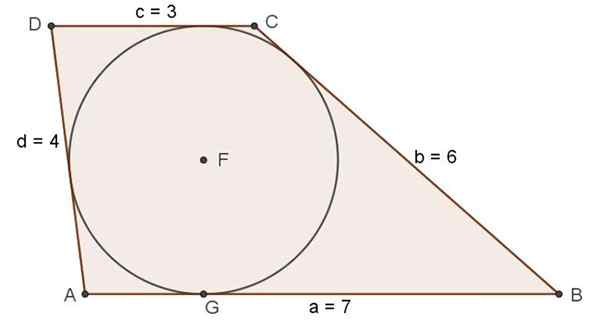Figure 7. Trapèze scalène qui répond à l'état d'existence de la circonférence enregistrée. Source: F. Zapata.

Exercice résolu

Déterminez les angles intérieurs du trapézoïde de base AB = A = 7, CD = C = 3 et BC latéral BC = B = 6, Da = D = 4.

Solution

Le théorème du cosinus peut être appliqué pour déterminer les angles. Par exemple, l'angle ∠a = α est déterminé à partir du triangle ABD avec ab = a = 7, bd = d2 = 8,49 et da = d = 4.

Le théorème du cosinus appliqué à ce triangle reste comme ceci:

d₂² = A² + d² - 2 ∙ a ∙ d ∙ cos (α), c'est-à-dire:

72 = 49 + 16-56 ∙ cos (α).

Lors du nettoyage, le cosinus de l'angle α est obtenu:

Cos (α) = -1/8

C'est-à-dire que α = arccos (-1/8) = 97,18⁰.

De la même manière, les autres angles sont obtenus, étant leurs valeurs:

β = 41,41⁰; γ = 138,59⁰ et enfin δ = 82,82⁰.

Les références

1. C. ET. POUR. (2003). Éléments de géométrie: avec des exercices et une géométrie de la boussole. Université de Medellin.
2. Campos, F., Cerecedo, f. J. (2014). Mathématiques 2. Groupe éditorial de Patria.
3. Libéré, k. (2007). Découvrir les polygones. Benchmark Education Company.
4. Hendrik, V. (2013). Polygones généralisés. Birkhäuser.
5. Iger. (s.F.). Mathématiques Premier semestre Tacaná. Iger.
6. JR. Géométrie. (2014). Polygones. Lulu Press, Inc.
7. Miller, Heeren et Hornsby. (2006). Mathématiques: raisonnement et applications (dixième édition). Pearson Education.
8. Patiño, m. (2006). Mathématiques 5. Progreso éditorial.
9. Wikipédia. Trapèze. Récupéré de: est.Wikipédia.com