Applications, exemples et exercices de la série Fourier résolus

Le Série de Fourier Ils consistent en une somme de termes infinis, qui se composent de fonctions harmoniques, le sinus et le cosinus, dont l'argument est un fond fondamental d'une fréquence fondamentale.

Les fonctions sinus et cosinus sont multipliées par des coefficients de valeurs, de sorte que la somme est identique à une fonction avec une période t égale à deux fois Pi (2π) divisé par la fréquence angulaire fondamentale ω ω ω.

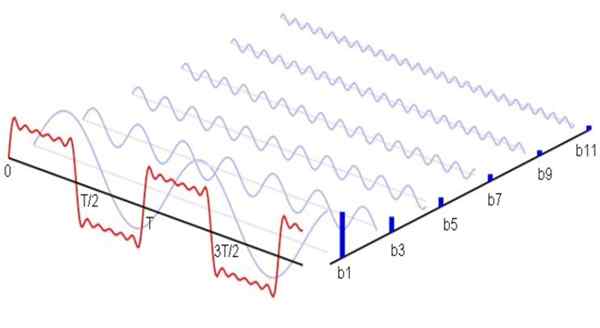
Figure 1. Voici (en bleu) les premières harmoniques non nuls de la série Fourier correspondant à un signal de forme d'onde carré. La somme que ces harmoniques donne naissance au signal rouge. Source: Wikimedia Commons.

Mathématiquement, il serait exprimé comme suit: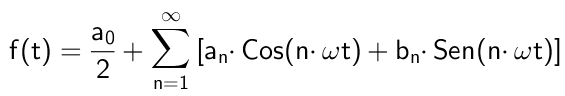

Où Ω C'est la fréquence fondamentale, qui est liée à la période T de la fonction f (t) À travers la relation: 

Ω = 2π / t

Pour une période périodique T, la fonction f (t) rencontre cette condition:

f (t) = f (t + k t)

Où k C'est un entier et les coefficients pour₀ , pour_n et B_n Ils sont appelés le Coefficients de Fourier.

[TOC]

Importance et utilisations des séries Fourier

Le nom de la série Fourier est dû au fait que son découvreur était le mathématique français.

Cette découverte était fondamentale pour les mathématiques, car si une équation différentielle a une solution harmonique particulière, il est possible d'atteindre la solution générale au moyen du chevauchement ou de la somme de la même.

Les coefficients de Fourier d'une fonction périodique, également appelés signe, Ils sont le spectre du même.

Par conséquent, le spectre est l'ensemble des fréquences qui constituent un signal caractérisé par l'amplitude de chaque fréquence, ce qui correspond aux valeurs des coefficients de Fourier.

Systèmes de compression de signal ou formes d'onde audio et vidéo, dans le dos nettement plus petit nombre de bits que le signal numérisé d'origine.

La série de Fourier d'un signal est comme ses empreintes digitales, en ce sens que, connu les coefficients qui le composent, vous pouvez toujours savoir quel signe ils appartiennent.

Bien que l'utilisation de la série Fourier, ou sa forme la plus générale, la Transformée de Fourier, En tant que méthode de compression de signal, elle est connue depuis un certain temps, son utilisation dans la pratique a dû attendre les processeurs numériques assez rapidement, ce qui a permis aux signaux d'être compressés et décompressés en "temps réel".

Peut vous servir: variables statistiques

Exemple de la série Fourier 

Ensuite, un exemple de fonction f (t) et de sa série Fourier.

La fonction est:

 f (t) = 0 oui 0 ≤ t  < π y 1 si π ≤  t   < 2π

Et a sa série Fourier correspondante donnée par:

f (t) = ½ - 2 / π⋅se (t) - 2 / (3π) ⋅se (3t) - 2 / (5π) ⋅sen (5t) - 2 / (7π) ⋅sen (7t) -…

La figure suivante montre la fonction et la somme partielle de la série Fourier:

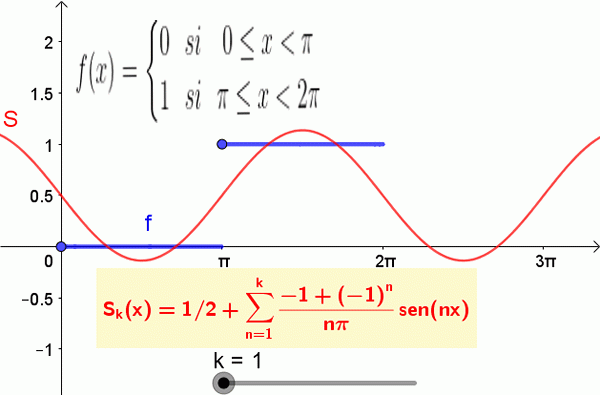Figure 2. Les 19 premiers termes de la somme de Fourier correspondant à la fonction de pas sont affichés. Source: F. Zapata.

Détermination des coefficients

Vous trouverez ci-dessous comment déterminer les coefficients de Fourier:

Supposons que la fonction soit F (x) définie dans un intervalle qui va de t_Toi à t_Toi + T, où le capital sera la période de la fonction. Ensuite, sa série de Fourier est:

f (t) = a₀ / 2 + a₁ cos (ω t) + a₂ cos (2 Ω t) +… + a_n Cos (n ω t) +…

.. .+ b₁ sin (ω t) + b₂ sin (2 ω t) +… + b_n Sin (n ω t) + ..

Calcul du terme indépendant

Pour trouver le terme indépendant, nous intégrons les deux membres de l'égalité dans l'intervalle de définition de la fonction:

[t_Toi , t_Toi+ T]

Donc:

Même_n ∫cos (n ω t) dt +…

.. .+ b₁ ∫sen (ω t) dt + b₂ ∫sen (2 Ω t) dt +… + b_n ∫sen (n ω t) dt +…

Ici, le symbole ∫ signifie intégral défini à partir de t_Toi à t_Toi + T.

L'intégrale du premier terme est T, qui lorsqu'elle est évaluée dans ses résultats de limite supérieure:

t_Toi + T

Lors de la soustraction de la limite inférieure t_Toi, dans définitif t.

Tous les autres termes sont 0, car ce sont des fonctions de cosinus ou de sinus évaluées en pleine période, comme nous le montrons ci-dessous:

∫cos (nω t) dt = (1 / nΩ) ∫cos (nΩ t) d (nω t)

N'oubliez pas que le symbole ∫ signifie l'intégration entre t_Toi à t_Toi + T. 

Pour faire l'intégration des termes qui ont le cosinus ou le sein, nous apporterons le changement de variable suivant:

x = ω (t - t_Toi)

Ainsi, le différentiel x, dx est égal à la différentiel d (ωt).

L'intégrale à effectuer est donc:

Comme n est un entier, alors l'intégrale définie donnera toujours zéro. Il en va de même pour la fonction sinusoïdale.

Par conséquent, l'intégrale définie évaluée dans une période complète de tous les termes contiennent. 

Peut vous servir: divisions dans lesquelles le résidu est de 300

Il est donc conclu que le terme a₀ est calculé comme suit:

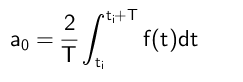
Calcul des coefficients à

Pour calculer les coefficients qui se multiplient aux fonctions du cosinus, les deux membres de l'égalité doivent être multipliés:

f (t) = a₀ / 2 + a₁ cos (ω t) + a₂ cos (2 Ω t) +… + a_n Cos (n ω t) +…

.. .+ b₁ sin (ω t) + b₂ sin (2 ω t) +… + b_n Sin (n ω t) + ..

Par la fonction cosinus évaluée dans l'harmonique correspondante, puis l'intégrale définie en pleine période aux deux membres est appliquée. 

Par exemple, pour calculer_m Les deux membres sont multipliés par COS (MΩT):

f (t) cos (m ω t) = a₀ / 2 cos (m ω t) + a₁ cos (ω t) cos (m ω t) + a₂ cos (2 ω t) cos (m ω t) +… + pour_n Cos (n ω t) cos (m ω t) +…

.. .+ b₁ sin (ω t) cos (m ω t) + b₂ sin (2 ω t) cos (m ω t) +… + b_n Sin (n ω t) cos (m ω t) + ..

Puis intégrer dans une période complète, c'est-à-dire dans l'intervalle qui va de t_Toi à t_Toi + T.

L'intégrale du terme contenant a₀ est annulée, car m est un entier et la fonction cosinus est intégrée dans une période complète. 

Les intégrales contenant le produit cos (n ω t) cos (m ω t) sont également annulées chaque fois que n ≠ m. Ce n'est que dans le cas que n = m a l'intégrale:

Tous les termes qui ont un sinus multiplié en cosinus, c'est-à-dire ceux qui sont multipliés par les coefficients de B, comme contenant des intégrales du type Sen (n ω t) cos (m ω t) sont annulées lorsque l'intégrale définie est effectuée sur un complet période. 

De là, il est conclu que:

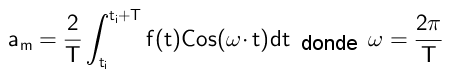
Calcul des coefficients b

Pour trouver les coefficients de B, une procédure similaire est appliquée, mais cette fois les deux membres de la fonction correspondant à la série Fourier sont multipliés par la fonction SEN (M ω T).

Pour les mêmes raisons déjà expliquées pour le cas dans lequel le seul terme qui n'est pas annulé après l'intégration dans une période complète est une période dans laquelle:

n = m

Et où l'intégrale de [Sen (m ω t)] apparaît]², qui intégré sur une période complète se traduit par π.

Peut vous servir: fonction homographique: comment graphiquement, exercices résolus

De cette façon, les coefficients de B sont calculés en fonction de la formule suivante:

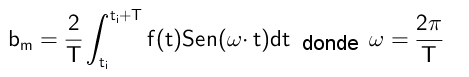
Exercices

- Exercice 1

Faire le calcul explicite des coefficients de la fonction

 f (t) = 0 oui 0 ≤ t  < π y 1 si π ≤  t   < 2π

Solution

Nous identifions d'abord la période t de cette fonction comme 2π, de sorte que la fréquence fondamentale ω = 2π / t dans cet exemple est égale à l'unité, c'est-à-dire:

Ω = 1

La fonction est définie dans l'intervalle [0, 2π], donc toutes les intégrations seront effectuées dans ledit intervalle. 

Ensuite, le terme indépendant est calculé comme suit:

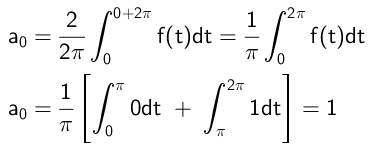
Les coefficients qui se multiplient aux fonctions cosinus sont calculés de cette manière:

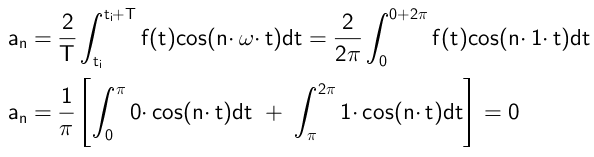
Comme on peut le voir, tous les coefficients sont nuls, ce qui se produira à condition que la fonction f (t) soit étrange.

De même, les coefficients de B seront calculés comme suit:

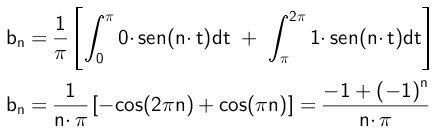
- Exercice 2

Trouvez les coefficients de la fonction correspondant à la figure 1, qui est:

f (t) = -1 oui 0≤ t

Solution 

Comme la fonction prend des valeurs entre -1 et +1, nous pouvons intuiti que le terme indépendant est vide, mais nous le calculerons explicitement:

En raison du fait que la fonction a une symétrie étrange, tous les coefficients qui multiplient les termes harmoniques avec la fonction cosinus doivent être vides. Nous le vérifions ci-dessous:

Enfin, nous trouverons les coefficients de B qui multiplient les termes harmoniques qui contiennent la fonction sinusale:

Où tous les termes de B avec l'indice UP peuvent être remarqués sont 0. Les premiers termes étranges sont:

b₁= -4 / (π); b₃= -4 / (3π); b₅= -4 / (5π); b₇= -4 / (7π) et b₉= -4 / (9π)

https: // youtu.Être / 737yagwszya

Les références

1. Amherror, je. 2013. Master la transformation discrète de Fourier en une, deux ou plusieurs dimensions: les pièges et les artefacts. Springer Science & Business Media.
2. Briggs, w. Année mille neuf cents quatre-vingts-quinze. Le DFT: un manuel des propriétaires pour la transformée de Fourier discrète. Siam.
3. Chu, e. 2008. Transformes de Fourier discrètes et continues: analyse, applications et algorithmes rapides. CRC Press.
4. Guoan BI, Yonghong Zeng. 2012. Transforme et algorithmes rapides pour l'analyse et les représentations du signal. Springer Science & Business Media.
5. Sundararajan, D. 2003. Traitement du signal numérique: théorie et pratique.Scientifique du monde. 
6. Wikipédia. Série de Fourier. Récupéré de: est.Wikipédia.com