Distribution de fréquence Comment faire un tableau, exemple, exercice

Ongle Distribution de fréquence En statistiques, il fait référence à la tendance qui suit les données organisées en groupes, catégories ou classes, lorsque chacun se voit attribuer un numéro appelé fréquence, ce qui indique le nombre de données dans chaque groupe. 

En règle générale, il est observé que ces fréquences sont distribuées autour d'un groupe central: celui avec le plus grand nombre de données.

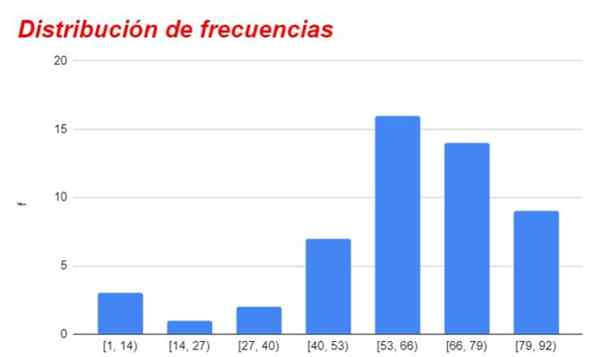
Figure 1. Tableau de distribution de fréquence obtenu à partir de son tableau correspondant. Source: F. Zapata.

Les groupes supérieurs ou inférieurs à ladite catégorie centrale diminuent progressivement leur fréquence, étant très petite ou insignifiante pour les catégories la plus éloignée de la catégorie avec une fréquence plus élevée.

La façon de connaître la distribution de fréquence d'un ensemble de données consiste d'abord à créer les catégories et à faire le tableau de fréquence. La représentation visuelle du tableau de fréquences est appelée histogramme.

[TOC]

Types de fréquences

Il existe plusieurs types de fréquences:

1.- Frecuence absolue: C'est le plus basique, et à partir de là, les autres sont construits. Il se compose simplement du nombre total de données correspondant à une catégorie.

2.- Fréquence relative: C'est la fréquence absolue de chaque catégorie divisée par le nombre total de données.

3.- Pourcentage de fréquence: C'est la même fréquence relative mais multiplié par cent, indiquant le pourcentage de valeurs d'apparence dans chaque catégorie.

4.- Fréquence accumulée: C'est la somme des fréquences absolues des catégories inférieures ou égales à la catégorie envisagée. 

5.- Pourcentage de fréquence accumulée: C'est la somme des fréquences en pourcentage des catégories inférieures ou égales à la catégorie observée.

Étapes pour faire un tableau de distribution de fréquence

Il y a plusieurs étapes à suivre pour construire un tableau de distribution de fréquences.

En premier lieu, les données doivent un arbre, etc.

Peut vous servir: quels sont les diviseurs de 30? (Explication)

Étape 1

Identifier la valeur minimale Xmin et la valeur maximale Xmax Dans l'ensemble de données X.

Étape 2

Calculez la plage R, qui est définie comme la différence entre la valeur maximale moins la valeur minimale: r = xmax - xmin.

Étape 3

Déterminer le nombre k d'intervalles ou de classes, qui peuvent être pré-établies. Le numéro k déterminera le nombre de lignes que le tableau de fréquence aura.

Étape 4

Dans le cas du nombre d'intervalles k Il n'est pas donné auparavant, alors il doit être établi conformément aux directives suivantes: le moins de catégories recommandées est de 5, mais elle peut être plus élevée, auquel cas il est préférable de choisir un nombre impair.

Étape 5

Il y a une formule appelée Règle des Sturges qui nous donne le nombre d'intervalles k recommandé pour un ensemble composé de N données:

K = [1 + 3 322⋅log n]

Comme le résultat dans le support sera sûrement un nombre réel, le support indique qu'il doit être arrondi à l'entier impair le plus proche pour obtenir une valeur entière de k.

Étape 6

L'amplitude est calculée POUR de chaque intervalle (classes ou catégories) prenant le quotient entre la gamme R et le nombre d'intervalles k: A = r / k. Si les données d'origine sont des nombres entiers, alors l'entier le plus proche est arrondi, sinon sa valeur réelle est laissée.

Étape 7

Déterminez les limites inférieures et supérieures de chaque intervalle ou classe. Le premier intervalle, ou la classe la plus basse, a comme limite inférieure la plus petite des données d'origine, c'est-à-dire Li = xmin et comme limite supérieure, la valeur minimale plus l'amplitude de l'intervalle, c'est ls = xmin + a. 

Étape 8

Les intervalles successifs sont: 

[Xmin, xmin + a), [ Xmin + a, xmin + 2⋅a), ... [ Xmin + (k-1) a, xmin + k⋅a).

Peut vous servir: opérations combinées

Étape 9

La marque de classe XC est déterminée pour chaque intervalle, en utilisant la formule suivante: Xc = (ls - li) / 2 + li.

Étape 10

L'en-tête du tableau de fréquence est placé, qui se compose d'une ligne avec les étiquettes suivantes: classes, marque de classe XC, fréquence F, fréquence relative F (ou pourcentage de fréquence F%) et fréquence accumulée F (ou pourcentage accumulé Fréquence F%).

Ce que nous aurons ensuite, c'est le suivant:

Première colonne du tableau de fréquence: contient les intervalles ou les classes dans lesquelles les données ont été divisées.

Deuxième colonne: contient la marque de classe (ou point intermédiaire) de chaque sous-intervalle.

Troisième colonne: Contient la fréquence absolue F de chaque classe ou catégorie.

Quatrième et cinquième colonne: Les valeurs correspondant à la fréquence relative (ou à pourcentage) et la fréquence accumulée F (ou pourcentage accumulé) sont placées.

Exemple de construction de table

Les données suivantes correspondent aux réponses précises à 100 questions appliquées à un groupe de 52 étudiants:

65, 70, 70, 74, 61, 77, 85, 36, 70, 62, 62, 77, 80, 89, 39, 43, 70, 77, 79, 77, 88, 52, 85, 1, 55, 55, 47, 73, 63, 59, 51, 56, 65, 85, 79, 53, 79, 3, 71, 7, 54, 8, 61, 61, 77, 67, 58, 61, 45, 48, 64, 15, 50.

Nous suivrons les étapes pour construire le tableau de fréquence:

1.- Valeurs minimales et maximales xmin = 1, xmax = 89.

2.- La plage est: r = 89 - 1 = 88

3.- Détermination du nombre d'intervalles selon le Règle des Sturges: K = [1 + 3 322⋅log 52] = [6,70] = 7.

4.- Calcul de la largeur des intervalles: a = r / k = 88/7 = 12,57 ≈ 13.

5.- Les intervalles sont: [1,14), [14, 27), [27, 40), [40, 53), [53, 66), [66, 79), [79, 92).

6.- Les marques de classe de chaque intervalle sont déterminées: 8, 21, 34, 47, 60, 73 et 86.

7.- La table est faite:

Peut vous servir: angles conjugués internes et externes: exemples, exercices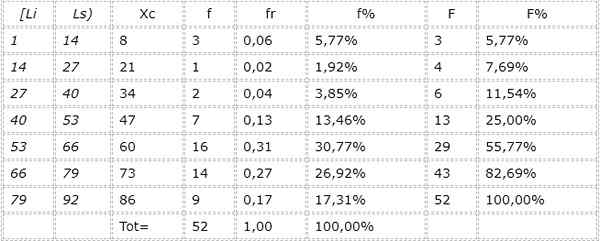

Le graphique des fréquences pour les différents intervalles ou catégories est illustré à la figure 1.

Exercice résolu

Un enseignant enregistre le pourcentage d'objectifs atteints dans le sujet de la physique pour chaque élève. Cependant, la qualification à chaque étudiant, bien qu'elle dépend du pourcentage d'objectifs atteints, est serré à certaines catégories précédemment établies dans le Règlement sur les études universitaires.

Regardons un cas spécifique: dans une section de physique, vous avez le pourcentage d'objectifs atteints pour chacun des 52 étudiants: 

15, 50, 62, 58, 51, 61, 62, 74, 65, 79, 59, 56, 77, 8, 55, 70, 7, 36, 79, 61, 77, 52, 35, 43, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61. 65, 70, 89, 64, 54, 85, 61, 39, 63, 70, 85, 70, 79, 48, 77, 73, 67, 45, 77, 71, 53, 88, 85, 47, 73, 77, 80.

Dans cet exemple, les catégories ou classes correspondent à la qualification finale attribuée en fonction du pourcentage x des objectifs atteints:

1.- Très pauvre: 1 ≤ x < 30

2.- Pauvre: 30 ≤ x < 50

3.- Assez: 50 ≤ x < 70

4.- Eh bien: 70 ≤ x < 85

5.- Excellent: 85 ≤ x ≤ 100

Pour faire le tableau des fréquences, les données sont commandées du moins au plus grand et indiquent combien de données correspondent à chaque catégorie, qui sera la qualification que l'étudiant obtiendra dans le sujet de la physique:

1.- Très pauvre: 4 étudiants.

2.- Pauvre: 6 étudiants.

3.- Assez: 20 étudiants.

4.- Eh bien: 17 étudiants.

5.- Excellent: 5 étudiants.

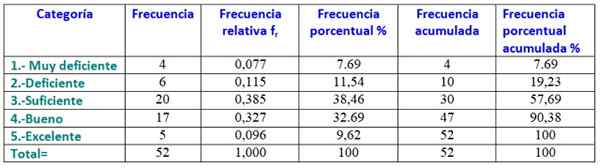
Ci-dessous, l'histogramme des grades, construit à partir du tableau précédent:

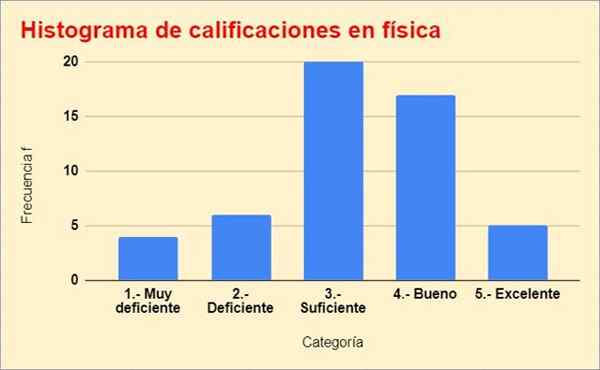Figure 2. Graphique de distribution de fréquence de l'exercice résolu. Source: F. Zapata.

Les références

1. Berenson, M. 1985. Statistiques pour l'administration et l'économie. Inter-américain s.POUR.
2. Canavos, g. 1988. Probabilité et statistiques: applications et méthodes. McGraw Hill.
3. Devore, J. 2012. Probabilité et statistiques pour l'ingénierie et la science. 8e. Édition. Cengage.
4. Levin, R. 1988. Statistiques pour les administrateurs. 2e. Édition. Prentice Hall.
5. Spiegel, m. 2009. Statistiques. Série Schaum. 4 ta. Édition. McGraw Hill.
6. Walpole, R. 2007. Probabilité et statistiques pour l'ingénierie et la science. Pearson.