Types de sections coniques, applications, exemples

Le sections coniques Ce sont les courbes qui sont obtenues en interceptant un avion avec un cône. Il y a plusieurs moyens de le faire; Par exemple, si le plan est passé perpendiculairement à l'axe axial du cône, une circonférence est obtenue.

L'inclinaison de l'avion un peu par rapport à l'axe axial du cône, une ellipse est obtenue, une courbe qui est fermée, mais si nous l'informons encore plus une parabole ou une hyperbole est obtenue, comme on peut le voir dans l'animation de la figure 1.

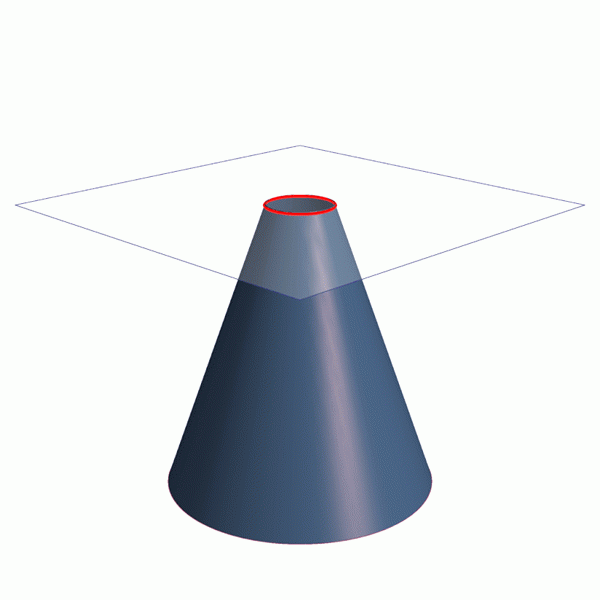Animation qui montre comment obtenir les quatre sections coniques: circonférence, parabole et hyperbola ellipse. Source: Wikimedia Commons. Lignes / cc0

Les sections coniques font partie de la nature et du monde qui nous entoure. L'ingénierie, l'architecture et l'astronomie sont des branches importantes de la connaissance qui font des utilisations des coniques.

[TOC]

Conditions pour les sections coniques

Les sections coniques sont définies comme des lieux géométriques qui satisfont aux conditions suivantes:

Parabole

C'est le lieu géométrique de tous les points qui se trouvent dans un plan équidistant à un point fixe appelé se concentrer F et une ligne droite également fixe, appelée directif.

Ellipse

Un point plan appartient à une ellipse si la somme des distances entre ce point et deux autres points fixes, appelés Focos et situé sur le axe majeur de l'ellipse, reste constant.

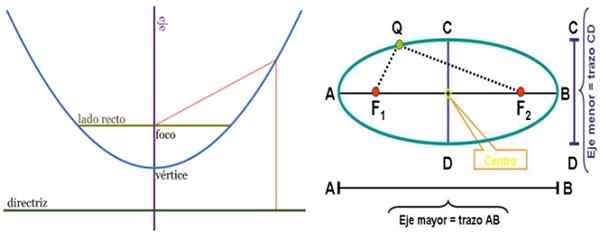La parabole à gauche et l'ellipse à droite, avec leurs éléments respectifs. Les foyers sont des points avec de nombreuses applications. Source: Wikimedia Commons.

Circonférence

C'est le lieu géométrique de tous les points qui maintiennent la même distance à un autre point appelé Centro. Cette distance est la radio de la circonférence.

Peut vous servir: distance euclidienne: concept, formule, calcul, exemple

Hyperbole

Ensemble de points dans le plan de telle sorte que la différence entre sa distance à deux points fixes appelés Focos, C'est constant.

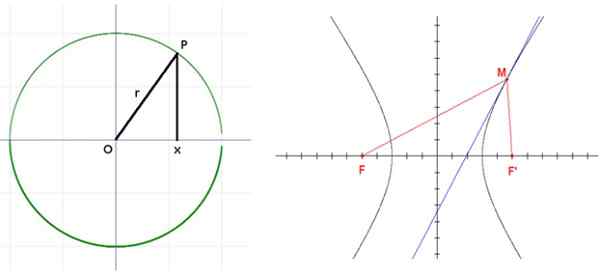Hyperbole avec foys f et f. Source: Wikimedia Commons.

Applications

Examinons certaines des applications de sections coniques:

Paraboles  

-Lorsqu'un objet est lancé, la trajectoire qui suit a une forme de parabole.

-Les paraboles ont des applications d'ingénierie notables, par exemple dans les ponts suspendus, les câbles se dépêchent sous forme de paraboles.

-Les paraboles sont également bonnes pour fabriquer des réflecteurs et des télescopes. Cela est grâce à une propriété intéressante: lors de la mise en place d'un luminaire au centre d'une surface de section transversale parabolique, la lumière se déplacera dans des rayons parallèles à l'axe de la parabole.

-Si les rayons lumineux parallèles à l'axe de symétrie s'approchent de la surface parabolique, il les concentre dans l'orientation, une circonstance utilisée pour faire des télescopes de réflecteur, comme le télescope Hale de Monte Palomar.

Ellipses

-Les planètes du système solaire se déplacent après les trajectoires elliptiques, assez près de la circonférence dans le cas des principales planètes, le terrain comprenait. Le soleil n'est pas au centre, mais dans l'un des projecteurs.

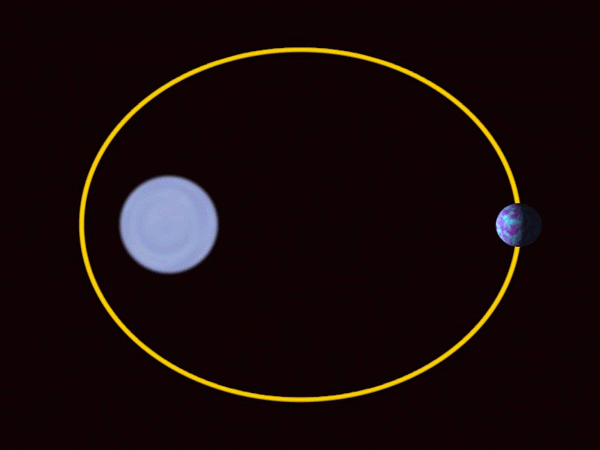Les planètes du système solaire se déplacent dans des orbites elliptiques avec le soleil dans l'un des projecteurs. Source: Wikimedia Commons.

-L'ellipse est largement utilisée dans l'architecture comme élément décoratif et design.

-En plaçant un réflecteur dans l'un des projecteurs d'une ellipse, la lumière se reflète vers l'autre foyer. La même chose se produit avec le son. C'est pourquoi dans les salles en forme d'Ellipse, qui parlent tranquillement dans un objectif sont clairement entendues par les auditeurs situés dans l'autre foyer.

Cela peut vous servir: prisme hépagonal

-Cette même propriété a une application surprenante dans le domaine de la médecine. Les calculs rénaux peuvent être détruits par le son. Des vagues échographiques d'une grande intensité sont générées dans l'un des foyers d'une baignoire elliptique pleine d'eau, et le patient est situé dans l'autre focus. Les ondes sonores affectent et réfléchissent dans le calcul, et avec leur énergie, ils le fragment en petits morceaux, ce que la personne expulse alors facilement pendant la miction.

Hyperboles

-Certaines comètes dans le système solaire suivent les trajectoires hyperboliques, toujours avec le soleil dans l'un des foyers.

-Les concentrations hyperbolas sont également très intéressantes pour étudier les phénomènes de la réflexion des vagues. Par exemple, en dirigeant un faisceau de lumière vers le centre d'un miroir parabolique, il se reflète dans l'autre foyer, une propriété très utile pour construire des télescopes, car la lumière peut se concentrer sur un miroir parabolique et être redirigé vers un autre endroit plus approprié selon le design.

-Les tours de refroidissement des centrales nucléaires ont une silhouette en forme d'hyperbolas.

-Avant l'avènement du GPS, les hyperbolas ont été utilisés dans la navigation pour localiser les bateaux. Les navires transportés à bord des signaux publiés simultanément par les stations radio A et B et un ordinateur étaient responsables de l'enregistrement des différences des heures d'arrivée des signaux, pour les transformer en différences de distances. De cette façon, le navire est situé dans la branche d'une hyperbole.

La procédure est répétée avec deux autres stations radio C et D, qui place le navire dans la branche de Une autre hyperbole. La position définitive du bateau est l'intersection des deux hyperbolas.

Peut vous servir: fonction de croissance: comment l'identifier, des exemples, des exercices

Circonférences

-L'arrivée de la roue a changé le cours de l'histoire.

-Le mouvement circulaire est très courant, de nombreuses pièces tournent pour produire divers effets, des usines aux ventilateurs.

-Bien que les trajectoires des principales planètes soient elliptiques, les trajectoires circulaires sont de bonnes approches dans de nombreux cas.

-Les circonférences sont des éléments fréquents en architecture, conception, ingénierie et construction. La liste des formes circulaires ou disques est infinie: pièces de monnaie, CD, montres et plus.

Exemples

Ensuite, il y a deux coniques dans l'avion, un cercle et une ellipse.

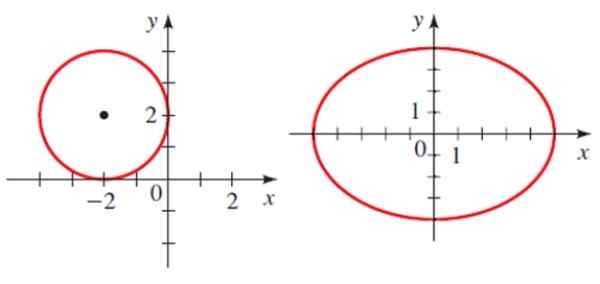Exemples de sections coniques: un cercle et une ellipse. Source: Stewart, J. Précalation.

Chacun a une équation analytique:

Circonférence

(X-H)² + (et K)² = R²

Où H et K sont les coordonnées du centre et R est la radio. Pour la circonférence illustrée dans la figure, l'équation est:

(x + 2)² + (Y-2)² = 4

Ellipse

L'équation de l'ellipse dont le centre est le point de coordonnées (h, k):

[(X-H)² /pour² ] + [(y-k)² / b² ] = 1

Où a et b sont les semi-piles de l'ellipse. Pour l'ellipse montré, le centre est au point 0,0, le plus grand semi -laire est le même et la semi-je mineure est 4. Par conséquent, son équation est:

(X² / 25) + (et² / 16) = 1

Les références

1. Hoffman, J. Sélection de problèmes de mathématiques. 2ieme volume.
2. Jiménez, R. 2008. Algèbre. Prentice Hall.
3. Stewart, J. 2006. Précaulement: mathématiques pour le calcul. 5e. Édition. Cengage Learning.
4. Wikipédia. Section conique. Récupéré de: est.Wikipédia.org.
5. Zill, D. 1984. Algèbre et trigonométrie. McGraw Hill.