U -Test de Mann - Whitney ce qui est et quand s'applique, exécution, exemple

La U -Test de Mann - Whitney Il est appliqué pour comparer deux échantillons indépendants lorsqu'ils ont peu de données ou ne suivent pas de distribution normale. De cette façon, il est considéré comme un test pas paramétrique, Contrairement à votre homologue Test de l'étudiant, qui est utilisé lorsque l'échantillon est suffisamment grand et suit la distribution normale.

Frank Wilcoxon le propose pour la première fois en 1945, pour des échantillons de tailles identiques, mais deux ans plus tard, il a été étendu dans le cas d'échantillons de taille différente par Henry Mann et D. R. Whitney.

Figure 1. Le test U de Mann - Whitney est appliqué pour la comparaison des échantillons indépendants. Source: Pixabay.

Le test est souvent appliqué pour vérifier s'il existe une relation entre une variable qualitative et un autre quantitatif.

Un exemple illustratif est de prendre un ensemble de personnes hypertensives et d'extraire deux groupes, à qui les données quotidiennes de la pression artérielle sont enregistrées pendant un mois.

À un groupe le traitement A et un autre est appliqué le traitement b. Ici, la pression artérielle est la variable quantitative et le type de traitement est le qualitatif.

Vous voulez savoir si la médiane, et non la moyenne, des valeurs mesurées est statistiquement égale ou différente, pour déterminer s'il existe une différence entre les deux traitements. Pour obtenir la réponse, le Wilcoxon ou U -Test de Mann - Whitney est appliqué.

[TOC]

Approche problème dans le test U de Mann - Whitney

Un autre exemple dans lequel le test peut être appliqué est le suivant:

Supposons que vous souhaitiez savoir si la consommation de boissons gazeuses diffère considérablement dans deux régions du pays.

L'un d'eux s'appelle la région A et l'autre région B. Un enregistrement des litres consommés chaque semaine dans deux échantillons est réalisé: l'une des 10 personnes pour la région A et une autre de 5 personnes pour la région B.

Les données sont les suivantes:

-Région A: 16, 11, 14, 21, 18, 34, 22, 7, 12, 12

-Région B: 12,14, 11, 30, 10

La question suivante est soulevée:

La consommation de boissons gazeuses (y) dépend-elle de la région (x)?

Variables qualitatives par rapport aux variables quantitatives

-Variable qualitative x: Région

-Variable quantitative et: Consommation gazeuse

Si la quantité de litres consommée est la même dans les deux régions, la conclusion sera qu'il n'y a pas de dépendance entre les deux variables. La façon de savoir est de comparer la tendance moyenne ou médiane pour les deux régions.

Cas normal

Si les données suivent une distribution normale, deux hypothèses sont augmentées: le H0 nul et l'alternative H1 à travers la comparaison entre les moyennes:

Peut vous servir: produits notables

-H0: Il n'y a pas de différence entre la moyenne des deux régions.

-H1: Les moyens des deux régions sont différentes.

Cas sans tendance normale

Au contraire, si les données ne suivent pas une distribution normale ou si simplement l'échantillon est très petit à savoir, au lieu de comparer la moyenne, elle serait comparée La médiane des deux régions.

-H0: Il n'y a pas de différence entre la médiane des deux régions.

-H1: Les médianes des deux régions sont différentes.

Si les médianes coïncident, alors l'hypothèse nulle est réalisée: il n'y a pas de relation entre la consommation de soda et la région.

Et si l'inverse se produit, l'hypothèse alternative est vraie: il existe une relation entre la consommation et la région.

C'est pour ces cas où le test U de Mann - Whitney est indiqué.

Échantillons ou échantillons non paires

Le problème important suivant pour décider si le test U de Mann Whitney est appliqué, c'est si le nombre de données dans les deux échantillons est identique, ce qui équivaut à dire qu'ils sont en même temps.

Si les deux échantillons sont appariés, la version originale de Wilcoxon s'appliquerait. Mais sinon, comme c'est le cas de l'exemple, le test de Wilcoxon modifié est appliqué, qui est précisément le test U de Mann Whitney.

Caractéristiques de test de Mann Whitney U

Le test U de Mann - Whitney un test non paramétrique, applicable aux échantillons qui ne suivent pas la distribution normale ou avec peu de données. Il a les caractéristiques suivantes:

1.- Comparez les médianes

2.- Fonctionne sur les gammes ordonnées

3.- Il est moins puissant, compréhensif par le pouvoir de la probabilité de rejeter l'hypothèse nulle alors qu'en réalité c'est faux.

En tenant compte de ces caractéristiques, le test U de Mann - Whitney est appliqué lorsque:

-Les données sont indépendantes

-Ils ne suivent pas la distribution normale

-L'hypothèse nul H0 est acceptée si le médium des deux échantillons coïncide: ma = Mb

-L'hypothèse alternative H1 est acceptée si le milieu des deux échantillons diffère: ma ≠ mb

Formule Mann - Whitney

La variable U est la statité de contraste utilisée dans le test Mann - Whitney et elle est définie:

U = min (ua, ub)

Cela signifie que u est le moindre des valeurs entre UA et UB, appliquée à chaque groupe. Dans notre exemple, ce serait à chaque région: a o b.

Les variables UA et UB sont définies et calculées en fonction de la formule suivante:

Ua = nb + na (na +1) / 2 - ra

Ub = nb + nb (nb +1) / 2 - rb

Peut vous servir: réduction de termes similaires

Ici, les valeurs Na et Nb sont les tailles des échantillons correspondant aux régions A et B respectivement et en revanche, Ra et Rb sont les sommets que nous définirons ci-dessous.

Étapes pour appliquer le test

1.- Commandez les valeurs des deux échantillons.

2.- Affecter une plage de commande à chaque valeur.

3.- Corriger les ligatures existantes dans les données (valeurs répétées).

4.- Calculer RA = somme des gammes de l'échantillon A.

5.- Trouver RB = somme des gammes de l'échantillon B.

6.- Déterminez la valeur UA et UB, selon les formules données dans la section précédente.

7.- Comparez UA et UB, et le mineur des deux est affecté à la statistique ou à la statistique expérimentale (c'est-à-dire les données) par rapport à la statistique théorique ou normale.

Application pratique de l'application

Maintenant, nous appliquons la susmention au problème du soda précédemment soulevé:

Région A: 16, 11, 14, 21, 18, 34, 22, 7, 12, 12

Région B: 12,14, 11, 30, 10

Selon que les moyens des deux échantillons sont statistiquement identiques ou différents, nous acceptons ou rejetons l'hypothèse nulle: il n'y a pas de relation entre la variable et X, c'est-à-dire que la consommation de soda ne dépend pas de la région:

H0: MA = MB

H1: ma ≠ mb

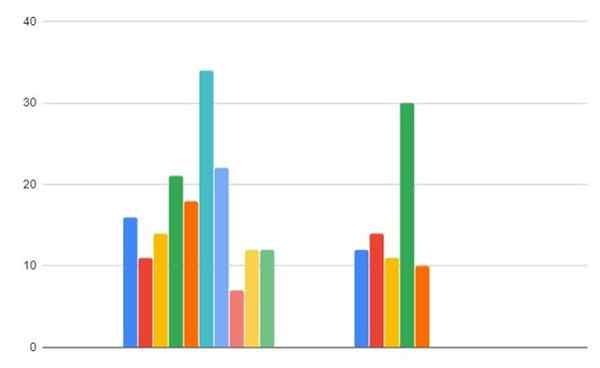Figure 2. Données de consommation gazeuse dans les régions A et B. Source: F. Zapata.

- Étape 1

Nous procédons à l'ordre des données conjointement pour les deux échantillons, commandant les valeurs du moins au plus grand:

Notez que la valeur 11 apparaît 2 fois (une fois dans chaque échantillon). À l'origine, il a des positions ou des gammes 3 et 4, mais pour surestimer ou sous-estimer l'une ou l'autre, la valeur moyenne est choisie comme portée, soit 3,5.

De même, la valeur 12 est prolongée, qui est répétée trois fois avec des plages de 5, 6 et 7.

Eh bien, la valeur 12 se voit attribuer la plage moyenne de 6 = (5 + 6 + 7) / 3. Et la même chose pour la valeur 14, qui a la ligature (apparaît dans les deux échantillons) dans les positions 8 et 9, la plage moyenne 8 est attribuée.5 = (8 + 9) / 2.

- Étape 2

Les données pour les régions A et B sont ensuite séparées à nouveau, mais maintenant leurs gammes correspondantes sont attribuées dans une autre ligne:

Région A

Région B

Les gammes RB sont obtenues à partir des sommes des éléments de la deuxième ligne pour chaque cas ou région.

Étape 3

Les valeurs UA et UB respectives sont calculées:

UA = 10 × 5 + 10 (10 + 1) / 2 - 86 = 19

Ub = 10 × 5 + 5 (5 + 1) / 2 -34 = 31

Valeur expérimentale u = min (19, 31) = 19

Étape 4

Le théoricien est censé suivre une distribution normale n avec des paramètres donnés exclusivement par la taille des échantillons:

Peut vous servir: nombres irrationnels: histoire, propriétés, classification, exemples

N ((na⋅nb) / 2, √ [nb (na + nb +1) / 12])

Afin de comparer la variable ou l'obtention expérimentale, avec celle théorique, il est nécessaire de faire un changement variable. Il passe de la variable ou expérimentale à sa valeur caractérisé, qui sera appelé Z, Afin de pouvoir comparer avec celui d'une distribution normale caractérisée.

Le changement variable est le suivant:

Z = (u - na.Nb / 2) / √ [na. Nb (na + nb + 1) / 12] 

Il convient de noter que pour le changement de variable, les paramètres de la distribution théorique pour u ont été utilisés. Ensuite, la nouvelle variable Z, qui est un hybride entre le théorique et la distribution expérimentale ou normale normifiée n (0,1).

Critères de comparaison

Si z ≤ zα ⇒ L'hypothèse nul H0 est acceptée

Oui z> zα ⇒ L'hypothèse nul H0 est rejetée

Les valeurs critiques typifiées dépendent du niveau de confiance requis, par exemple pour un niveau de confiance α = 0,95 = 95% qui est le plus habituel a la valeur critique zα = 1,96.

Pour les données présentées ici:

Z = (u - nb / 2) / √ [nb (na + nb + 1) / 12] = -0,73

Qui est en dessous de la valeur critique 1.96.

Alors la conclusion finale est que l'hypothèse nulle est acceptée:

Il n'y a pas de différence dans la consommation de soude entre les régions A et B.

Calculateurs en ligne pour le test U de Mann - Whitney

Il existe des programmes spécifiques pour les calculs statistiques, y compris SPSS et Minitab, mais ces programmes sont payés et leur utilisation n'est pas toujours simple. En effet, ils donnent tellement d'options que son utilisation est pratiquement réservée aux experts en statistique.

Heureusement, il existe plusieurs programmes en ligne très précis, gratuits et simples qui permettent entre autres les tests U -Whitney U.

Ces programmes sont:

-Statistiques des sciences sociales (Socscistatistics.com), qui a à la fois le test U-Whitney U et Wilcoxon dans le cas d'échantillons équilibrés ou appariés.

-Statistiques de thérapie IA (IA-thérapie.com), qui a plusieurs des tests de statistiques descriptifs habituels.

-Statistique à utiliser (physique.Csbsju.Edu / statistiques), l'un des plus anciens, afin que votre interface puisse sembler obsolète, bien qu'il s'agisse d'un programme gratuit très efficace.

Les références

1. Dietrichson. Méthodes quantitatives: Test de gammes. Récupéré de: bookdown.org
2. Marín J P. Guide SPSS: Analyse et procédures dans les tests non paramétriques. Récupéré de: halweb.Uc3m.est
3. USAL MOOC. Test non paramétrique: U de Mann - Whitney. Récupéré de: youtube.com
4. Wikipédia. U -Test de Mann - Whitney. Récupéré de: est.Wikipédia.com
5. Xlstat. Centre d'aide. Tutoriel de test de Mann - Whitney dans Excel. Récupéré de: aide.Xlsat.com