Formules et équations d'erreur d'échantillonnage, calcul, exemples
- 3524
- 768
- Anaïs Julien
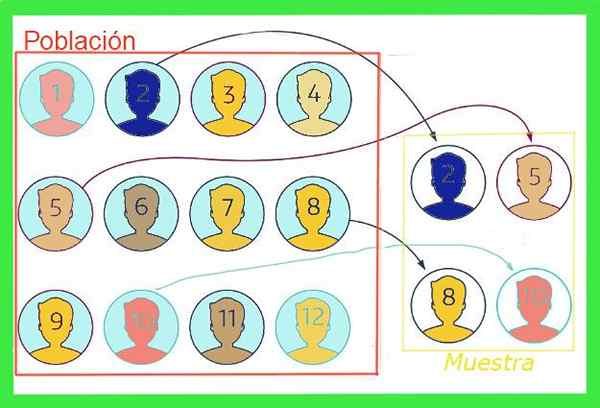
Il erreur d'échantillonnage soit exemple d'erreur En statistiques, c'est la différence entre la valeur moyenne d'un échantillon par rapport à la valeur moyenne de la population totale. Pour illustrer l'idée, imaginons que la population totale d'une ville est d'un million, dont vous voulez ses chaussures moyennes, pour lesquelles mille personnes sont prélevées à un échantillon aléatoire.
La taille moyenne résultant de l'échantillon ne coïncidera pas nécessairement avec celle de la population totale, bien que si l'échantillon n'est pas biaisé, la valeur doit être proche. Cette différence entre la valeur moyenne de l'échantillon et celle de la population totale est l'erreur de l'échantillon.
 Figure 1. Comme l'échantillon est un sous-ensemble de la population totale, la moyenne de l'échantillon a une marge d'erreur. Source: F. Zapata.
Figure 1. Comme l'échantillon est un sous-ensemble de la population totale, la moyenne de l'échantillon a une marge d'erreur. Source: F. Zapata. En général, la valeur moyenne de la population totale est inconnue, mais il existe des techniques pour réduire ces erreurs et formules pour estimer le Exemple de marge d'erreur qui sera exposé dans cet article.
[TOC]
Formules et équations
Mettons-nous au cas où vous souhaitez connaître la valeur moyenne d'une certaine fonctionnalité mesurable X Dans une population de taille N, mais comment N C'est un grand nombre n'est pas viable d'étudier la population totale, nous procédons donc à un échantillon de taille n<
La valeur moyenne de l'échantillon est indiquée par et la valeur moyenne de la population totale le dénote pour la lettre grecque μ (ça se lit Mu ou miu).
Supposons qu'ils soient pris m Échantillons de population totaux N, Toute taille égale n Avec des valeurs moyennes
Ces valeurs moyennes ne seront pas identiques les unes aux autres et seront toutes autour de la valeur de la population moyenne μ. Il Exemple de marge d'erreur E indique la séparation attendue des valeurs moyennes par rapport à la Valeur de population moyenne μ dans un pourcentage spécifié appelé le Niveau de confiance γ (Gamma).
Peut vous servir: additif inverseIl Marge d'erreur standard ε de l'échantillon de taille n est:
ε = σ / √n
où σ est l'écart type (La racine carrée de la variance), qui est calculée par la formule suivante:
σ = √ [(x -)2/ (N - 1)]
Le sens de Marge d'erreur standard ε est le suivant:
Il valeur moyenne obtenu par l'échantillon de taille n est compris dans l'intervalle (- ε, + ε) avec un un niveau de confiance 68,3%.
Comment calculer l'erreur d'échantillonnage
Dans la section précédente, la formule a été donnée pour trouver le marge d'erreur standard d'un échantillon de n, où le mot standard indique qu'il s'agit d'une marge d'erreur avec 68% de confiance.
Cela indique que si de nombreux échantillons de la même taille ont été prélevés n, 68% d'entre eux donneront des valeurs moyennes dans la plage [- ε, + ε].
Il y a une règle simple, appelée le Règle 68-95-99.7 qui nous permet de trouver la marge de Exemple d'erreur E Pour des niveaux de confiance de 68%, 95% et 99,7% facilement, car cette marge est 1⋅ε, 2⋅ε et 3⋅ε respectivement.
Pour un niveau de confiance γ
Si il Niveau de confiance γ Ce n'est pas ce qui précède, donc l'erreur d'échantillonnage est l'écart type σ multiplié par le facteur Zγ, qui est obtenu par le biais de la procédure suivante:
1.- Premièrement la niveau de signification α qui est calculé à partir de Niveau de confiance γ À travers la relation suivante: α = 1 - γ
Peut vous servir: Théorème de Bayes2.- Alors vous devez calculer la valeur 1 - α / 2 = (1 + γ) / 2, qui correspond à la fréquence normale accumulée entre -∞ et Zγ, Dans une distribution normale ou gaussienne caractérisée f (z), dont la définition peut être observée dans la figure 2.
3.- L'équation est résolue F (zγ) = 1 - α / 2 À travers les tables de distribution normales (accumulées) F, o via une application informatique qui a la fonction gaussienne inverse typique F-1.
Dans ce dernier cas, vous avez:
Zγ = g-1(1 - α / 2).
4.- Enfin, cette formule d'erreur d'échantillonnage avec un niveau de fiabilité est appliquée γ:
E = zγ⋅(σ / √n)
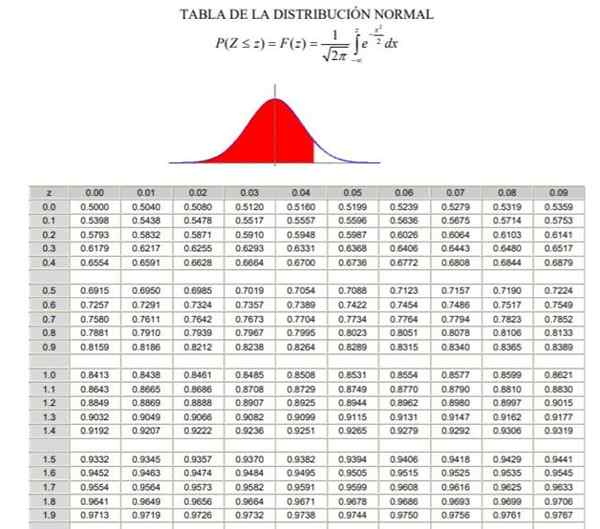 Figure 2. Tableau de distribution normal. Source: Wikimedia Commons.
Figure 2. Tableau de distribution normal. Source: Wikimedia Commons. Exemples
- Exemple 1
Calculez le Marge d'erreur standard Sur le poids moyen d'un échantillon de 100 nouveau-nés. Le calcul du poids moyen était = 3 100 kg avec un écart-type σ = 1 500 kg.
Solution
Il Marge d'erreur standard est ε = σ / √n = (1 500 kg) / √100 = 0,15 kg. Ce qui signifie qu'avec ces données, on peut en déduire que le poids de 68% des nouveau-nés se situe entre 2 950 kg et 3.25 kg.
- Exemple 2
Déterminer la marge de l'échantillon d'erreur et et la plage de poids de 100 nouveau-nés avec un niveau de confiance à 95% si le poids moyen est de 3 100 kg avec un écart-type σ = 1 500 kg.
Solution
Si la Règle 68; 95; 99.7 → 1⋅ε; 2⋅ε; 3⋅ε, Tu as:
E = 2⋅ε = 2⋅0,15 kg = 0,30 kg
En d'autres termes, 95% des nouveau-nés auront des pesos entre 2 800 kg et 3 400 kg.
- Exemple 3
Déterminez la gamme en pesos de nouveau-nés de l'exemple 1 avec une marge de confiance de 99,7%.
Peut vous servir: Rhomboid: caractéristiques, comment éliminer le périmètre et la zoneSolution
L'erreur de l'échantillon avec une confiance de 99,7% est 3 σ / √n, que pour notre exemple est E = 3 * 0,15 kg = 0,45 kg. De là, il est déduit que 99,7% des nouveau-nés auront des pesos entre 2 650 kg et 3 550 kg.
- Exemple 4
Déterminer le facteur Zγ Pour un niveau de fiabilité de 75%. Déterminez la marge d'erreur d'échantillonnage avec ce niveau de fiabilité pour le cas soulevé dans l'exemple 1.
Solution
Il un niveau de confiance est γ = 75% = 0,75 qui se rapporte au niveau de signification α à travers la relation γ= (1 - α), de sorte que le niveau de signification est α = 1 - 0,75 = 0,25.
Cela signifie que la probabilité normale accumulée entre -∞ et Zγ est:
P (Z ≤ Zγ ) = 1 - 0,125 = 0,875
Ce qui correspond à une valeur Zγ de 1 1503, comme le montre la figure 3.
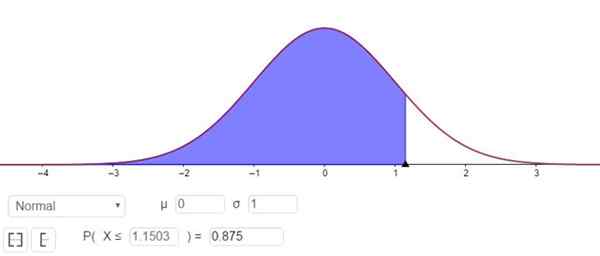 figure 3. Détermination du facteur Zγ correspondant à un niveau de confiance de 75%. Source: F. Zapata à travers Geogebra.
figure 3. Détermination du facteur Zγ correspondant à un niveau de confiance de 75%. Source: F. Zapata à travers Geogebra. En d'autres termes, l'erreur d'échantillonnage est E = zγ⋅(σ / √n)= 1.15⋅(σ / √n).
Lorsqu'il est appliqué aux données de l'exemple 1, il donne une erreur de:
E = 1,15 * 0,15 kg = 0,17 kg
Avec un niveau de confiance de 75%.
- Exercice 5
Quel est le niveau de confiance si zα / 2 = 2.4 ?
Solution
P (z ≤ zα / 2 ) = 1 - α / 2
P (z ≤ 2.4) = 1 - α / 2 = 0,9918 → α / 2 = 1 - 0,9918 = 0,0082 → α = 0,0164
Le niveau de signification est:
α = 0,0164 = 1,64%
Et enfin, le niveau de confiance reste:
1- α = 1 - 0,0164 = 100% - 1,64% = 98,36%
Les références
- Canavos, g. 1988. Probabilité et statistiques: applications et méthodes. McGraw Hill.
- Devore, J. 2012. Probabilité et statistiques pour l'ingénierie et la science. 8e. Édition. Cengage.
- Levin, R. 1988. Statistiques pour les administrateurs. 2e. Édition. Prentice Hall.
- Sudman, s.1982. Poser des questions: un guide pratique de la conception du questionnaire. San Francisco. Jossey Bass.
- Walpole, R. 2007. Probabilité et statistiques pour l'ingénierie et la science. Pearson.
- Wonnacott, t.H. et r.J. Wonnacott. 1990. Statistiques d'introduction. 5e ed. Wiley
- Wikipédia. Exemple d'erreur. Récupéré de: dans.Wikipédia.com
- Wikipédia. Marge d'erreur. Récupéré de: dans.Wikipédia.com
- « Historique des statistiques inférenties, caractéristiques, à quoi sert, exemples
- U -Test de Mann - Whitney ce qui est et quand s'applique, exécution, exemple »

