Exemples de données groupés et exercice résolu

Les données groupées Ce sont ceux qui ont classé en catégories ou en cours, en prenant comme critère leur fréquence. Cela se fait dans le but de simplifier la gestion de grandes quantités de données et d'établir leurs tendances.

Une fois organisé dans ces classes pour leurs fréquences, les données constituent un Distribution de fréquence, à partir de laquelle les informations sur les services publics sont extraites par ses caractéristiques.

Figure 1. Avec les données groupées, vous pouvez créer des graphiques et calculer les paramètres statistiques qui décrivent les tendances. Source: Pixabay.

Ensuite, nous verrons un exemple simple de données groupées:

Supposons que la stature de 100 étudiantes, sélectionnées parmi tous les cours de physique de base d'une université, est mesurée et les résultats suivants sont obtenus:

Les résultats obtenus ont été divisés en 5 classes, qui apparaissent dans la colonne de gauche.

La première classe, entre 155 et 159 cm, compte 6 élèves, la deuxième classe 160 - 164 cm compte 14 élèves, la troisième classe de 165 à 169 cm est celle avec le plus grand nombre de membres: 47. Ensuite, suivez la classe de 170-174 cm avec 28 étudiants et enfin celui de 175 à 179 cm avec seulement 5.

Le nombre de membres de chaque classe est précisément le fréquence soit Frecuence absolue Et en les ajoutant tous, les données totales sont obtenues, ce qui dans cet exemple est 100.

[TOC]

Caractéristiques de distribution de fréquence

Fréquence

Comme nous l'avons vu, la fréquence est le nombre de fois qu'un fait est répété. Et pour faciliter les calculs des propriétés de distribution, tels que la moyenne et la variance, les quantités suivantes sont définies:

-Fréquence accumulée: Il est obtenu en ajoutant la fréquence d'une classe avec la fréquence accumulée antérieure. La première de toutes les fréquences coïncide avec celle de l'intervalle en question, et le dernier est le nombre total de données.

-Fréquence relative: Il est calculé en divisant la fréquence absolue de chaque classe par le nombre total de données. Et si vous multipliez par 100, vous avez le pourcentage de pourcentage de fréquence.

Peut vous servir: fonctions vectorielles

-Fréquence relative accumulée: C'est la somme des fréquences relatives de chaque classe avec l'accumulation précédente. Le dernier des fréquences relatives accumulées doit être égale à 1.

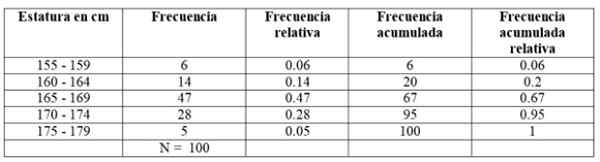
Pour notre exemple, les fréquences sont comme ceci:

Limites

Les valeurs extrêmes de chaque classe ou intervalle sont appelées Limites de classe. Comme nous pouvons le voir, chaque classe a une limite inférieure et une plus grande. Par exemple, la première classe de l'étude sur les statistiques a une limite inférieure à 155 cm et une plus de 159 cm.

Cet exemple a des limites qui sont clairement définies, mais c'est possible.

Les frontières

La hauteur est une variable continue, il peut donc être considéré que la première classe commence réellement en 154.5 cm, car en arrondissant cette valeur à l'entier le plus proche, 155 cm est obtenu.

Cette classe couvre toutes les valeurs jusqu'à 159.5 cm, car à partir de cela, les statues sont arrondies à 160.0 cm. Une stature de 159.7 cm appartient déjà à la classe suivante.

Les frontières de la classe réelles de cet exemple sont, en CM:

• 154.5 - 159.5
• 159.5 - 164.5
• 164.5 - 169.5
• 169.5 - 174.5
• 174.5 - 179.5

Amplitude

L'étendue d'une classe est obtenue en soustrayant les frontières. Pour le premier intervalle de notre exemple, vous avez 159.5 - 154.5 cm = 5 cm.

Le lecteur peut vérifier que pour les autres intervalles de l'exemple, l'amplitude résulte également de 5 cm. Cependant, il convient de noter que les distributions peuvent être construites avec des intervalles d'amplitude différente.

Il peut vous servir: règle t: caractéristiques, afin que ce soit, des exemples

Marque de classe

C'est le point moyen de l'intervalle et est obtenu par la moyenne entre la limite supérieure et la limite inférieure.

Pour notre exemple, la marque de première classe est (155 + 159) / 2 = 157 cm. Le lecteur peut vérifier que les marques de classe restantes sont: 162, 167, 172 et 177 cm.

La détermination des marques de classe est importante, car elles sont nécessaires pour trouver la moyenne arithmétique et la variance de la distribution.

Mesures de la tendance centrale et de la dispersion pour les données groupées

Les mesures de tendance centrale les plus utilisées sont moyennes, médianes et mode, et décrivent précisément la tendance des données à être regroupées autour d'une certaine valeur centrale.

Moitié

C'est l'une des principales mesures de tendance centrale. Dans les données groupées, la moyenne arithmétique peut être calculée à l'aide de la formule:

 Où:

-X est la moyenne

-F_Toi est la fréquence de la classe

-m_Toi C'est la marque de classe

-G est le nombre de classes

-n est le nombre total de données

Médian

Pour la médiane, vous devez identifier l'intervalle où se trouve l'observation N / 2. Dans notre exemple, cette observation est le numéro 50, car il y a un total de 100 données. Cette observation est dans l'intervalle 165-169 cm.

Ensuite, vous devez interpoler pour trouver la valeur numérique qui correspond à cette observation, pour laquelle la formule est utilisée:

Où:

-C = largeur d'intervalle où se trouve la médiane

-B_M = La bordure inférieure de l'intervalle à laquelle appartient la médiane

-F_m = quantité d'observations contenues dans l'intervalle médian

-N / 2 = la moitié du total des données

-F_BM = Nombre total d'observations avant l'intervalle médian

Mode

Pour la mode, la classe modale est identifiée, celle qui contient la plupart des observations, dont la marque de classe est connue.

Peut vous servir: pyramide hexagonale

Variance et écart-type

La variance et l'écart type sont des mesures de dispersion. Si nous désignons la variance avec S² Et à l'écart type, qui est la racine carrée de la variance comme S, pour les données groupées que nous aurons respectivement:

ET

Exercice résolu

Pour la distribution de la stature des étudiants universitaires proposés au début, calculez les valeurs de:

a) moyen

b) moyen

c) mode

d) variance et écart type.

Figure 2. En ce qui concerne beaucoup de valeurs, comme les statistiques d'un grand groupe d'étudiants, il est préférable de regrouper les données dans les classes. Source: Pixabay.

Solution à

Construisons le tableau suivant pour faciliter les calculs:

Grâce à l'expression du groupe moyen groupé ci-dessus:

Remplacement des valeurs et réalisant directement la somme:

X = (6 x 157 + 14 x 162 + 47 x 167 + 28 x 172+ 5 x 177) / 100 cm =

= 167.6 cm

Solution B

L'intervalle à lequel appartient la médiane est de 165-169 cm car c'est l'intervalle le plus fréquemment.

Identifions chacune de ces valeurs dans l'exemple, à l'aide du tableau 2:

C = 5 cm (voir la section d'amplitude)

B_M = 164.5 cm

F_m = 47

N / 2 = 100/2 = 50

F_BM = 20

Remplacement dans la formule:

Solution C

L'intervalle contenu dans la plupart des observations est de 165 à 169 cm, dont la marque de classe est de 167 cm.

Solution d

Nous élargissons le tableau précédent en ajoutant deux colonnes supplémentaires:

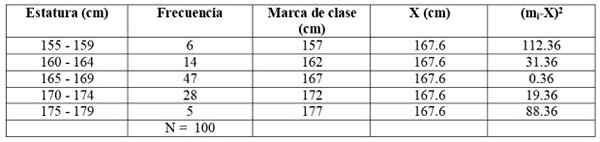
Nous appliquons la formule:

Et nous développons la somme:

s² = (6 x 112.36 + 14 x 31.36 + 47 x 0.36 + 28 x 19.36 + 5 x 88.36) / 99 = = 21.35 cm²

Donc:

S = √21.35 cm² = 4.6 cm

Les références

1. Berenson, M. 1985. Statistiques pour l'administration et l'économie. Inter-américain s.POUR.
2. Canavos, g. 1988. Probabilité et statistiques: applications et méthodes. McGraw Hill.
3. Devore, J. 2012. Probabilité et statistiques pour l'ingénierie et la science. 8e. Édition. Cengage.
4. Levin, R. 1988. Statistiques pour les administrateurs. 2e. Édition. Prentice Hall.
5. Spiegel, m. 2009. Statistiques. Série Schaum. 4 ta. Édition. McGraw Hill.
6. Walpole, R. 2007. Probabilité et statistiques pour l'ingénierie et la science. Pearson.