Caractéristiques de programmation dynamique, exemple, avantages, inconvénients

La Programmation dynamique Il s'agit d'un modèle d'algorithme qui résout un problème complexe en le divisant en sous-problèmes, en stockant leurs résultats afin d'éviter d'avoir à calculer ces résultats.

Ce programme est utilisé lorsque les problèmes peuvent être divisés en sous-problèmes similaires, afin que leurs résultats puissent être réutilisés. Pour le plus majoritaire, ce programme est utilisé pour l'optimisation.

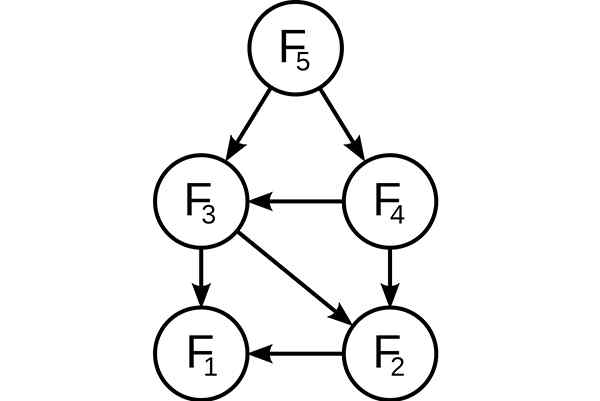
Programmation dynamique. Sous-problèmes superposés dans la succession de Fibonacci. Source: Wikimedia Commons, AT: Utilisateur: Dcoatzee, tracé par l'utilisateur: Domaine Stanered / Public

Avant de résoudre les sous-problèmes disponibles, l'algorithme dynamique essaiera d'examiner les résultats des sous-problèmes précédemment résolus. Les solutions de sous-problèmes sont combinées afin d'obtenir la meilleure solution.

Au lieu de calculer encore et encore le même sous-problème, votre solution peut être stockée dans une certaine mémoire, lorsque vous rencontrez ce sous-problème pour la première fois. Quand il réapparaît pendant la solution d'un autre sous-problème, la solution déjà stockée en mémoire sera prise.

C'est une idée merveilleuse pour corriger le temps avec la mémoire, où lorsque vous utilisez un espace supplémentaire, vous pouvez améliorer le temps nécessaire pour trouver une solution.

[TOC]

Caractéristiques de la programmation dynamique

Les caractéristiques essentielles suivantes sont celles qui peuvent être appliquées à un problème pour la programmation dynamique:

Substructure optimale

Cette caractéristique exprime qu'un problème d'optimisation peut être résolu en combinant les solutions optimales des problèmes secondaires qui compensent. Ces sous-structures optimales sont décrites par récursivité.

Par exemple, dans un graphique, une sous-structure optimale sera présentée sur la route la plus courte qui passe d'un sommet à un sommet T:

C'est-à-dire sur cette route la plus courte r, vous pouvez prendre n'importe quel sommet intermédiaire i. Si R est vraiment l'itinéraire le plus court, il peut être divisé en subrutas R1 (de S à i) et R2 (de i à t), de sorte que ce sont à leur tour les itinéraires les plus courts entre les sommets correspondants.

Par conséquent, pour trouver les voies les plus courtes, vous pouvez facilement formuler la solution récursivement, ce que fait l'algorithme Floyd-Warshall.

Sous-problèmes superposés

L'espace de sous-problèmes doit être petit. Autrement dit, tout algorithme récursif qui résout un problème doit résoudre les mêmes sous-problèmes encore et encore, au lieu de générer de nouveaux sous-problèmes.

Par exemple, pour générer la série Fibonacci, cette formulation récursive peut être considérée: fn = f (n-1) + f (n-2), en prenant comme cas de base qui f1 = f2 = 1. Alors vous devrez: F33 = F32 + F31 et F32 = F31 + F30.

Comme on peut le voir, F31 est résolu dans les saisons sous-marins récursives de F33 et F32. Bien que le nombre total de sous-problèmes soit vraiment faible, si une solution récursive est adoptée car cela finira par résoudre les mêmes problèmes encore et encore.

Peut vous servir: les 7 composants d'un système d'information

Ceci est pris en compte par programmation dynamique, donc il ne résout chaque sous-problème qu'une seule fois. Cela peut être réalisé de deux manières:

Approche supérieure

Si la solution à n'importe quel problème peut être formulée de manière récursive à l'aide de la solution de leurs sous-problèmes, et si ces sous-problèmes se chevauchent, les solutions aux sous-problèmes peuvent être facilement mémorisées ou stockées dans un tableau dans un tableau.

Chaque fois que la solution d'un nouveau sous-problème est recherchée, elle sera examinée dans le tableau si elle est précédemment résolue. Dans le cas où une solution est stockée, elle sera utilisée au lieu de la calculer à nouveau. Sinon, le sous-problème sera résolu, stockant la solution dans le tableau.

Approche ascendante

Une fois que la solution d'un problème est formulée de manière récursive en termes de sous-problèmes, le problème peut être essayé en ascendante: ils essaieront d'abord de résoudre les sous-problèmes et d'utiliser leurs solutions pour atteindre des solutions aux plus gros sous-problèmes.

Cela se fait également généralement sous la forme d'une table, générant des solutions itératives à des sous-problèmes de plus en plus importants en utilisant des solutions à de petits sous-problèmes. Par exemple, si les valeurs de F31 et F30 sont déjà connues, la valeur de F32 peut être calculée directement.

Comparaison avec d'autres techniques

Un appartenance significatif d'un problème qui peut être résolu par la programmation dynamique est qu'il devrait avoir des sous-problèmes qui se chevauchent. C'est ce qui distingue la programmation dynamique de la technique de division et de conquête, où il n'est pas nécessaire de stocker les valeurs les plus simples.

Il est similaire à la récursivité, car en calculant les cas de base, la valeur finale peut être déterminée par induction. Cette approche ascendante fonctionne bien lorsqu'une nouvelle valeur dépend uniquement des valeurs précédemment calculées.

Exemple

Étapes minimales pour atteindre 1

Pour tout numéro entier positif «E», vous pouvez effectuer l'une des trois étapes suivantes.

- Soustrayez 1 du numéro. (E = e-1).

- S'il est divisible par 2, il est divisé par 2 (si E% 2 == 0, alors e = e / 2).

- S'il est divisible par 3, il est divisé par 3 (si e% 3 == 0, alors e = e / 3).

Sur la base des étapes précédentes, vous devez trouver le montant minimum de ces étapes à prendre et 1. Par exemple:

- Si e = 1, résultat: 0.

- Si e = 4, résultat: 2 (4/2 = 2/2 = 1).

- Quand E = 7, résultat: 3 (7-1 = 6/3 = 2/2 = 1).

Approche

Vous pourriez toujours penser à choisir l'étape qui rend N aussi faible que possible et à continuer comme ça, jusqu'à ce qu'il atteigne 1. Cependant, on peut voir que cette stratégie ne fonctionne pas ici.

Peut vous servir: logiciel commercial

Par exemple, si E = 10, les étapes seraient: 10/2 = 5-1 = 4/2 = 2/2 = 1 (4 étapes). Cependant, la manière optimale est: 10-1 = 9/3 = 3/3 = 1 (3 étapes). Par conséquent, toutes les étapes possibles qui peuvent être faites pour chaque valeur de N doivent être prouvées, en choisissant le montant minimum de ces possibilités.

Tout commence par la récursivité: f (e) = 1 + min f (e-1), f (e / 2), f (e / 3) si e> 1, prenant comme cas de base: f (1 ) = 0. Ayant l'équation de récurrence, vous pouvez commencer à coder la récursivité.

Cependant, on peut observer qu'il a superposé des sous-problèmes. De plus, la solution optimale pour une entrée donnée dépend de la solution optimale de ses sous-problèmes.

Comme dans la mémorisation, où les solutions des sous-problèmes résolues sont stockées pour les utiliser plus tard. Ou comme dans la programmation dynamique, il commence par le bas, avançant vers le e donné. Ensuite, les deux codes:

Mémorisation

Programmation à la hausse dynamique

avantage

L'un des principaux avantages de l'utilisation de la programmation dynamique est qu'il accélère le traitement, car les références qui ont été précédemment calculées sont utilisées. Comme c'est une technique de programmation récursive, il réduit les lignes de code du programme.

Vorace Algoritmos vs Programmation dynamique

Les algorithmes voraces sont similaires à la programmation dynamique dans le sens où les deux sont des outils d'optimisation. Cependant, l'algorithme Voraz recherche une solution optimale à chaque étape locale. C'est-à-dire qu'il cherche un choix gourmand dans l'espoir de trouver un optimal mondial.

Par conséquent, les algorithmes voraces peuvent faire une hypothèse qui semble optimale à ce moment-là, mais qui devient cher à l'avenir et ne garantit pas un optimal mondial.

D'un autre côté, la programmation dynamique trouve la solution optimale pour les sous-problèmes, puis fait un choix éclairé en combinant les résultats de ces sous-problèmes pour vraiment trouver la solution la plus optimale.

Désavantages

- Beaucoup de mémoire est nécessaire pour stocker le résultat calculé de chaque sous-problème, sans pouvoir s'assurer que la valeur stockée sera utilisée ou non.

- Plusieurs fois, la valeur de sortie est stockée sans jamais être utilisée dans les sous-problèmes suivants pendant l'exécution. Cela conduit à une utilisation inutile de la mémoire.

- Dans la programmation dynamique, les fonctions sont appelées récursivement. Cela fait que la mémoire de la batterie reste constante.

Recursivité vs programmation dynamique

Si vous avez une mémoire limitée pour exécuter le code et que la vitesse de traitement n'est pas inquiétante, la récursivité peut être utilisée. Par exemple, si une application mobile est en cours de développement, la mémoire est très limitée pour exécuter l'application.

Peut vous servir: dispositifs mixtes: caractéristiques et exemples

Si le programme doit être exécuté plus rapidement et qu'il n'y a pas de restrictions de mémoire, il est préférable d'utiliser la programmation dynamique.

Applications

La programmation dynamique est une méthode efficace pour résoudre des problèmes qui pourraient autrement sembler extrêmement difficiles à résoudre dans un temps raisonnable.

Les algorithmes basés sur le paradigme de programmation dynamique sont utilisés dans de nombreux domaines scientifiques, y compris de nombreux exemples de l'intelligence artificielle, de la résolution des problèmes de planification à la reconnaissance vocale.

Algorithmes de programmation dynamique

La programmation dynamique est assez efficace et sert très bien pour un large éventail de problèmes. De nombreux algorithmes peuvent être vus comme des applications d'algorithmes voraces, tels que:

- Série Fibonacci Numbers.

- Towers Hanoi.

- Tous les routes les plus courtes se marient de Floyd-Warshall.

- Sac à dos.

- Programmation du projet.

- Le chemin le plus court de Dijkstra.

- Contrôle et contrôle des vols robotiques.

- Problèmes d'optimisation mathématique.

- Temps partagé: Programmez le travail pour maximiser l'utilisation du CPU.

Série Fibonacci Numbers

Les nombres de Fibonacci sont les nombres trouvés dans la séquence suivante: 0, 1, 1, 3, 5, 8, 13, 21, 34, 55, 89, 144, etc.

En terminologie mathématique, la succession FN des nombres de Fibonacci est définie par la formule de récidive: f (n) = f (n -1) + f (n -2), où f (0) = 0 et f (1) = 1.

Approche supérieure

Dans cet exemple, une matrice de recherche avec toutes les valeurs initiales est initialisée avec -1. Chaque fois que la solution à un sous-problème est nécessaire, elle sera d'abord recherchée dans cette matrice de recherche.

S'il y a la valeur calculée, cette valeur sera renvoyée. Sinon, le résultat sera calculé pour le stocker dans la matrice de recherche et ainsi le réutiliser plus tard.

Approche ascendante

Dans ce cas, pour la même série Fibonacci, F (0), puis F (1), F (2), F (3), et ainsi de suite est calculé en premier. Ainsi, les solutions des sous-problèmes du bas seront construites.

Les références

1. Vineet Choudhary (2020). Introduction à la programmation dynamique. Invité de non-élaboration.Tiré de: DeveloperriSider.co.
2. Alex Allain (2020). Programmation dynamique en C++. C programmation C. Pris de: cprogrammming.com.
3. After Academy (2020). Idée de programmation dynamique. Pris de: AfterAcademy.com.
4. Aniruddha Chaudhari (2019). Programmation et récursivité dynamiques | Différent. Pile CSE. Tiré de: csestack.org.
5. Code Chef (2020). Pour le tutoriel de programmation dynamique. Tiré de: CODHEF.com.
6. Programiz (2020). Programmation dynamique. Tiré de: Programiz.com.