Produit croisé

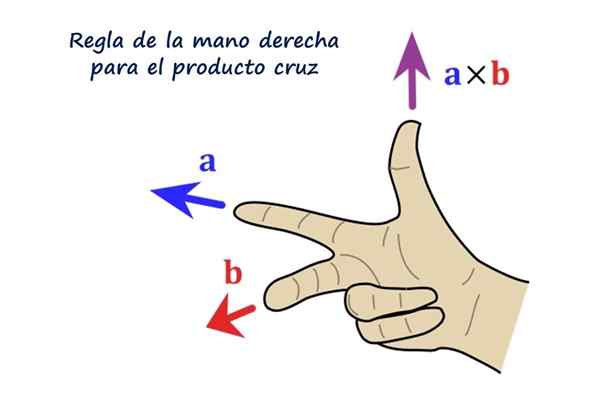Règle de droite pour le produit vectoriel. Source: F. Zapata.

Quel est le produit croisé ou le produit vectoriel?

Il Produit croisé, Également appelé produit vectoriel, il s'agit d'un type de produit qui est effectué entre deux vecteurs et qui se traduit par un autre vecteur, perpendiculaire au plan défini par les deux premiers.

Le produit croisé entre deux vecteurs pour et b, Il en résulte un autre vecteur R, Mathématiquement est écrit comme suit:

pour × b = R

Il se lit comme suit: «Un cruz b égal à r ".

En texte imprimé, les vecteurs sont écrits avec des paroles audacieuses, ou avec une flèche sur la lettre, pour les distinguer de leur ampleur ou de leur module. Pour cela, ils sont utilisés, de manière interchangeable, des barres de module et des lettres actuelles, donc la valeur absolue du vecteur pour Le symbole est écrit comme ceci:

│pour│ = A

La valeur ou le module absolu du produit vectoriel entre deux vecteurs est calculé en multipliant le module des deux vecteurs à travers l'angle θ entre eux:

R = a ∙ b ∙ Sen θ

La direction du vecteur R Il est perpendiculaire à celui des vecteurs pour et b. Le sens de R C'est dextrogyr de pour vers b Et en pratique, il est déterminé en utilisant la règle de la main droite, qui consiste à positionner l'indice, le milieu et le pouce de la main droite comme suit:

• L'index est placé après le vecteur pour
• Avec le majeur suit le vecteur b
• Le pouce, étendu, indique la direction et la direction du vecteur R.

Cette commande doit être suivie exactement, car le produit vectoriel n'est pas commutatif, c'est-à-dire pour × b ≠ b × pour Et si les vecteurs sont échangés, le résultat correct ne sera pas obtenu.

Peut vous servir: Théorème d'existence et d'unicité: démonstration, exemples et exercices

Il est conseillé au lecteur de placer sa main droite comme le montre la figure, l'indice pointant vers la gauche représente le vecteur pour, Le majeur suit b Et il pointe directement vers le lecteur, enfin, le pouce indique, pointant vers la direction et la direction du vecteur pour × b = R.

Propriétés du produit Cruz

-Le produit croisé ou vecteur entre deux vecteurs entraîne toujours un autre vecteur.

-Un produit croisé n'est pas commutatif, donc: pour × b ≠ b × pour.

-Pour le produit croisé, il est vrai que: pour × b = - (b × pour). Cette propriété est appelée anti-conmination.

-Le vecteur résultant du produit vectoriel entre deux vecteurs est perpendiculaire (normal) auxdits vecteurs.

-De ce qui précède, il s'ensuit que le produit vectoriel entre les vecteurs avec la même direction est nul. En particulier pour × A = 0.

-Le produit croisé est conforme à la loi sur la distribution en ce qui concerne la somme: pour × (b+c) = pour × b + pour × c

-Si m est un scalaire, alors m (pour × b) = m pour × b = pour × m b

Traverser le produit entre les vecteurs unitaires

Les trois vecteurs d'unité, appelés Toi, J et k, Ils sont perpendiculaires les uns aux autres et indiquent les trois directions notables de l'espace: haut, large et profondeur. Ces adresses sont perpendiculaires les unes aux autres.

Le produit vectoriel entre les vecteurs unitaires est facilement déterminé par la règle de droite et en gardant à l'esprit les propriétés du produit croisé:

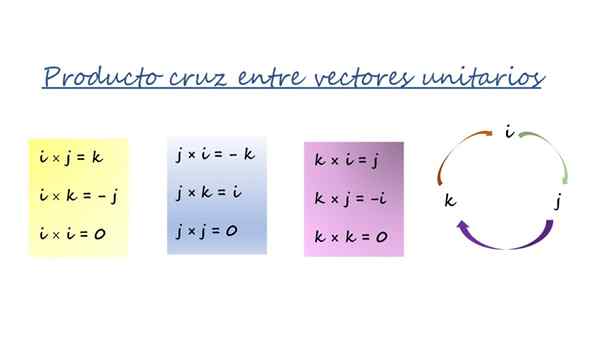Produit vecteur de vecteurs d'unité cartésienne. Source: F. Zapata.

Les trois boîtes colorées de la figure sont résumées dans le tour avec des flèches à droite et sont utilisées de cette manière:

-Lors de la multiplication dans le sens de la flèche, le résultat est le vecteur devant la flèche et a un signe positif. Par exemple, en multipliant vectoriel J et k, Le troisième vecteur est Toi, Et comme l'ordre suit le sens de la flèche, le signe est +.

Peut vous servir: fonctions vectorielles

-Et s'il se multiplie dans la direction opposée à la flèche, le résultat est le troisième vecteur devant la flèche, mais avec un signe négatif.

Les vecteurs unitaires constituent une base, de sorte que tout autre vecteur peut être écrit en termes d'eux. Cela facilite considérablement le calcul du produit transversal entre deux vecteurs arbitraires dans l'espace.

Comment analyser le produit transversal de deux vecteurs analytiquement

Quand les vecteurs pour et b Ils ont une direction arbitraire dans l'espace, avec des composants le long d'eux, il est plus facile de calculer le produit transversal de manière analytique, les exprimant en termes de vecteurs unitaires Toi, J et k:

• pour = A_X Toi + pour_et J + pour_z k
• b = b_X Toi + b_et J + b_z k

Maintenant, la propriété distributive de la multiplication est utilisée, ce qui est également valable pour le produit croisé:

pour × b = (a_X Toi + pour_et J + pour_z k) × (b_X Toi + b_et J + b_z k) =

= (a_X Toi × b_X Toi) + (a_X Toi × b_et J) + (a_X Toi × b_z k) + (a_ET J × b_X Toi) + (a_ET J × b_et J) + (a_ET J × b_z k) + (a_Z k × b_X Toi) + (a_Z k × b_et J) + (a_Z k × b_z k)

Les produits transversaux entre les vecteurs unitaires égaux sont annulés, car ce sont des vecteurs parallèles, ce qui réduit cette expression à 6 termes:

pour × b = (a_X Toi × b_et J) + (a_X Toi × b_z k) + (a_ET J × b_X Toi) + (a_ET J × b_z k) + (a_Z k × b_X Toi) + (a_Z k × b_et J)

Enfin, en utilisant la figure ci-dessus, chaque produit entraîne:

pour × b = A_X b_et k + pour_X b_z (-J) + a_ET b_X (-k) + a_ET b_z Toi + pour_Z b_XJ + pour_Z b_et (-Toi) =

= (a_ET b_z - un_Z b_et) Toi + (pour_Z b_X - un_X b_z) J + (pour_X b_et - un_ET b_X) k

Produit Cruz à travers un déterminant

Il n'est pas nécessaire de mémoriser la formule ci-dessus, mais d'appliquer commodément le tour de la figure précédente ou simplement de réaliser soigneusement le déterminant illustré ci-dessous, ce qui est totalement équivalent:

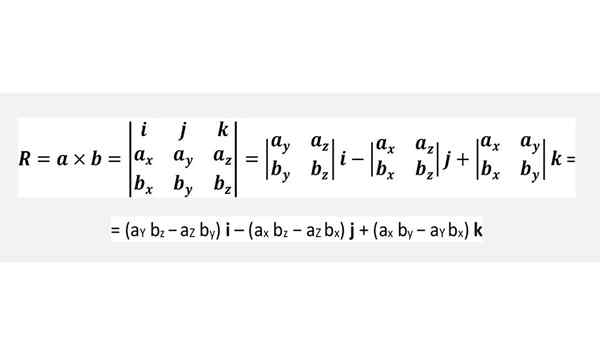
Exemple

En supposant des vecteurs pour et b ils sont:

• pour = 5 Toi - J + 4 k
• b = -Toi + 0J +7 k

Le produit croisé entre eux est calculé en identifiant et en remplacement des coordonnées respectives:

Peut vous servir: paraboloïde hyperbolique: définition, propriétés et exemples

pour_X = 5; pour_et = −1; pour_z = 4; b_X = −1; b_et = 0: b_z = 7

pour × b = [(−1) ∙ 7 - 4 ∙ 0] Toi + [(4 ∙ (−1) - 5 ∙ 7) J + [5 ∙ 0 - (−1) ∙ (−1)] k = [−7 - 0] Toi + [(−4 - 35) J + [0 - 1] k =

= (−7) Toi - 39 J - k

La méthode déterminante offre le même résultat.

Exercer

Calculez par déterminants, le produit croisé parmi les vecteurs:

• ou = 2 Toi +J + 5 k
• V = Toi + 4J +7 k

Et déterminer la zone du parallélogramme sous-tendu par les vecteurs précédents, comme indiqué sur la figure:

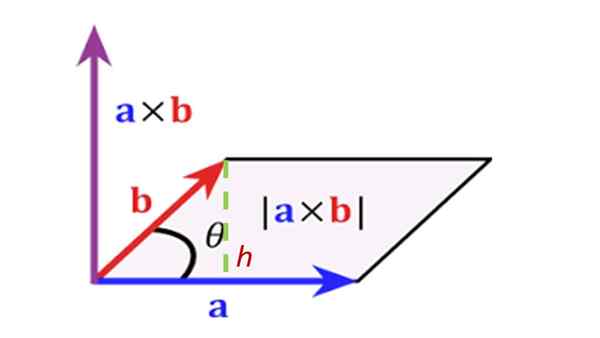
Solution

Les valeurs des coordonnées des vecteurs sont remplacées dans le déterminant:

La zone de parallélogramme déterminée est le module du produit vectoriel entre eux, résultant: r = 17,3 unités de zone.