Définition convexe du polygone, éléments, propriétés, exemples

UN polygone convexe C'est une figure géométrique contenue dans un plan caractérisé car il a toutes ses diagonales à l'intérieur et ses angles mesurent moins de 180º. Parmi ses propriétés figurent les suivantes:

1) Il se compose de N segments consécutifs où le dernier des segments rejoint le premier. 2) Aucun des segments n'est traversé de manière à délimiter le plan dans un intérieur et un autre extérieur. 3) chacun des angles de la région intérieure est strictement inférieur à un angle plat.

Figure 1. Les polygones 1, 2 et 6 sont convex. (Préparé par Ricardo Pérez).

Un moyen simple de déterminer si un polygone est convexe ou ne doit pas considérer la ligne qui passe à travers l'un de ses côtés, qui détermine deux semiplanes. Si sur chaque ligne qui passe d'une part, les autres côtés du polygone sont dans le même semi-semi, c'est alors un polygone convexe.

[TOC]

Éléments d'un polygone

Chaque polygone se compose des éléments suivants:

- Côtés

- Sommets

Les côtés sont chacun des segments consécutifs qui composent le polygone. Dans un polygone, aucun des segments qui le ralentit ne peut avoir une extrémité ouverte, dans ce cas, il y aurait une ligne polygonale mais pas un polygone.

Les sommets sont les points syndicaux de deux segments consécutifs. Dans un polygone, le nombre de sommets équivaut toujours au nombre de côtés.

Si deux côtés ou segments d'une croix de polygone, alors vous avez un polygone croix. Le point de croisement n'est pas considéré comme un sommet. Un polygone croix est un polygone non convexe. Les polygones écrasés sont des polygones croisés et ne sont donc pas convexes.

Il peut vous servir: géométrie analytique

Lorsqu'un polygone a tous ses côtés de la même longueur, il y a alors un polygone ordinaire. Tous les polygones ordinaires sont convexes. 

Polygones convexes et non convexes

La figure 1 montre plusieurs polygones, certains d'entre eux sont convexes et d'autres ne sont pas. Analysons-les:

Le numéro 1 est un polygone à trois côtés (triangle) et tous les angles internes sont inférieurs à 180 °, donc c'est un polygone convexe. Tous les triangles sont des polygones convexes.

Le numéro 2 est un polygone à quatre faces (quadrilatère) où aucun des côtés n'est intercepté et également chacun des angles intérieurs est inférieur à 180 °. Il s'agit alors d'un polygone convexe à quatre côtés (quadrilatère convexe).

D'un autre côté, le numéro 3 est un polygone à quatre faces, mais l'un de ses angles intérieurs est supérieur à 180 °, il ne répond donc pas à la condition de convexité. C'est-à-dire qu'il s'agit d'un polygone non convexe qui s'appelle un quadrilatère concave.

Le numéro 4 est un polygone à quatre segments (côtés), dont deux sont interceptés. Les quatre angles intérieurs sont inférieurs à 180 °, mais à mesure que les deux côtés se croisent, ils sont un polygone croix non convexe (quadrilatère transversal).

Un autre cas est le numéro 5. Il s'agit d'un polygone à cinq faces, mais comme l'un de ses angles intérieurs est supérieur à 180º, il y a alors un polygone concave.

Enfin, le numéro 6, qui a également cinq côtés, a tous ses angles intérieurs inférieurs à 180 °, il s'agit donc d'un polygone convexe à cinq faces (pentagone convexe).

Peut vous servir: Erreur d'échantillonnage: formules et équations, calcul, exemples

Propriétés convexes du polygone

1- Un polygone non croisé ou un polygone simple divise le plan qui le contient en deux régions. La région intérieure et la région extérieure, étant le polygone la frontière entre les deux régions.

Mais si en outre le polygone est convexe, alors il y a une région intérieure qui est simplement liée, ce qui signifie que prendre deux points de la région intérieure, il peut toujours être uni par un segment qui appartient à son intégralité à la région intérieure.

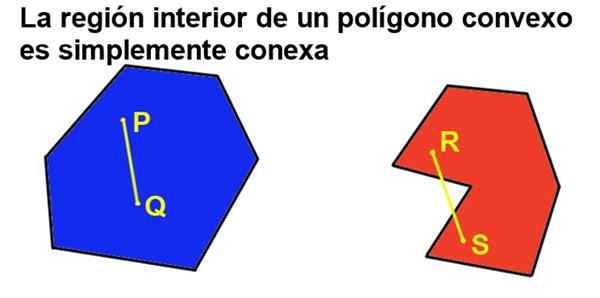Figure 2. Un polygone convexe est simplement lié, tandis qu'un concave n'est pas. (Préparé par Ricardo Pérez).

2- Tout l'angle intérieur d'un polygone convexe est inférieur à un angle plat (180º).

3- Tous les points intérieurs d'un polygone convexe appartiennent toujours à l'un des semi-définis par la ligne qui passe par deux sommets consécutifs.

4- Dans un polygone convexe, toutes les diagonales sont entièrement contenues dans la région du polygone intérieur.

5- Les points intérieurs d'un polygone convexe appartiennent à son intégralité au secteur angulaire convexe défini par chaque angle intérieur.

6- Chaque polygone dans lequel tous ses sommets se trouvent sur une circonférence est un polygone convexe appelé polygone cyclique.

7- Chaque polygone cyclique est convexe, mais chaque polygone convexe n'est pas cyclique.

8- Chaque polygone non croisé (polygone simple) qui a tous ses côtés de longueur égale est convexe et est connu sous le nom de polygone ordinaire.

Diagonales et angles dans les polygones convexes

9- Le nombre total de diagonales d'un polygone convexe de n côtés est donné par la formule suivante:

Il peut vous servir: graphismes polybal

N = ½ n (n - 3)

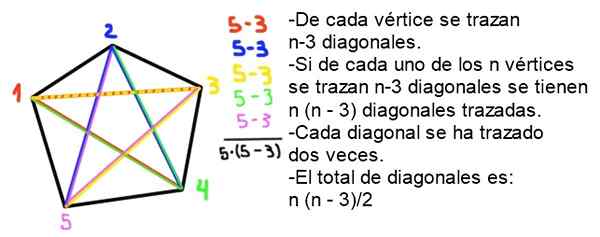
Démonstration: Dans un polygone convexe de n côtés de chaque sommet, N - 3 diagonales sont dessinées, car le sommet lui-même et les deux adjacents sont exclus. Comme il y a n sommets, ils sont dessinés en N - 2) des diagonales, mais chaque diagonale a été dessinée deux fois, de sorte que le nombre de diagonales (sans répétition) est n (n -2) / 2.

10- La somme des angles intérieurs d'un polygone convexe de n côtés est donné par la relation suivante:

S = (n - 2) 180º

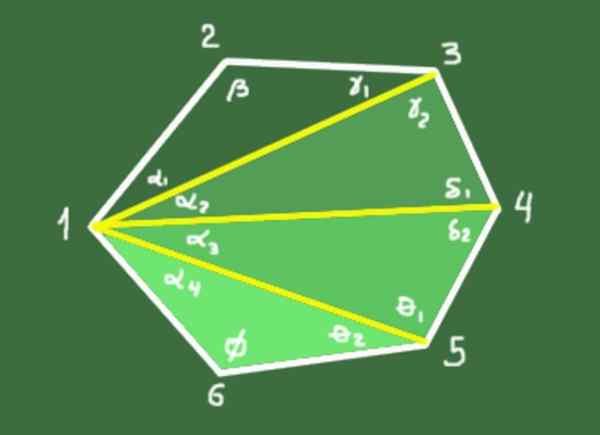
Démonstration: les diagonales N-3 sont tirées d'un sommet qui définissent les triangles N-2. La somme des angles internes de chaque triangle est de 180 °. La somme totale des angles des triangles N-2 est (N-2) * 180º, qui coïncide avec la somme des angles internes du polygone.

Exemples

Exemple 1

Hexagone cyclique, c'est un polygone à six côtés et six sommets, mais tous les sommets sont sur la même circonférence. Tout le polygone cyclique est convexe.

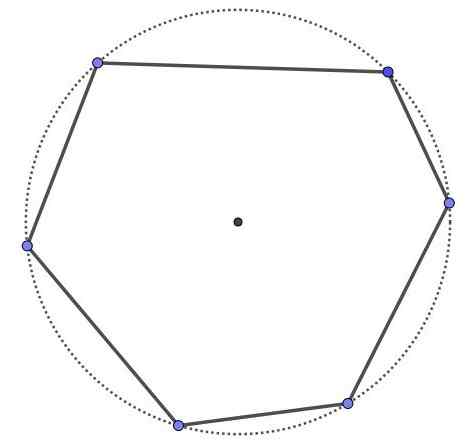Hexagone cyclique.

Exemple 2

Déterminez la valeur des angles internes d'une évente régulière.

Solution: Enegon est un polygone à 9 faces, mais il régule également tous ses côtés et les angles sont les mêmes.

La somme de tous les angles internes d'un polygone à 9 faces est:

S = (9 - 2) 180º = 7 * 180º = 1260º 

Mais il y a 9 angles internes de mesure égale α, donc l'égalité suivante doit être remplie:

S = 9 α = 1260º

De l'endroit où il s'ensuit que la mesure α de chaque angle interne de l'évégon ordinaire est:

α = 1260º / 9 = 140º