Numéros entiers

Quels sont les nombres entiers?

Les nombres entiers constituent un ensemble de nombres utiles pour compter les objets complets qui ont eu et ceux qui ne sont pas. Également pour compter ceux d'un côté et l'autre d'un certain lieu de référence.

De plus, avec l'ensemble des nombres, la soustraction ou la différence peut être effectuée entre un nombre et un autre plus grand que lui, étant réglé comme dette, par exemple. La distinction entre les bénéfices et les dettes est faite avec des signes + et - respectivement.

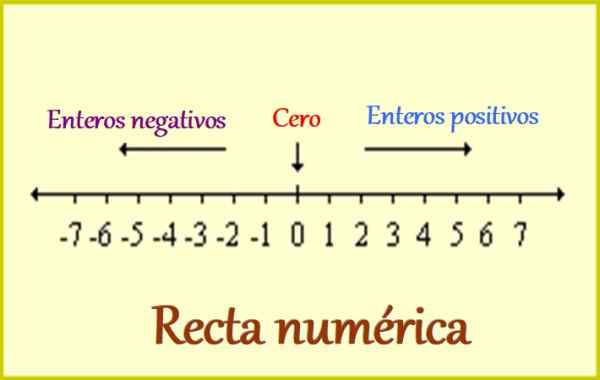
Figure 1. La ligne numérique pour les nombres entiers. Source: Wikimedia Commons. Leomg / cc by-sa (https: // CreativeCommons.Org / licences / by-sa / 3.0).

C'est pourquoi l'ensemble de l'ensemble des chiffres comprend les éléments suivants:

-Les entiers positifs, écrits précédés d'un signe +, ou simplement sans le signe, car il est également compris qu'ils sont positifs. Par exemple: +1, +2, +3 ... et ainsi de suite.

-Le 0, dans lequel le signe n'est pas pertinent, car il ne l'ajoute pas pour le soustraire d'un montant. Mais le 0 est très important, car c'est la référence pour les entiers: d'un côté, les positifs sont situés et les négatifs, comme nous le voyons dans la figure supérieure.

-Les entiers négatifs, qui doivent toujours être écrits à partir du signe -, car avec eux, les montants tels que les dettes et tous ceux qui se trouvent de l'autre côté de la référence sont distingués. Des exemples d'entiers négatifs sont: -1, -2, -3 ... et à partir de là.

Comment sont les nombres entiers?

Au début, nous représentons les nombres entiers avec le réglage de l'ensemble: z = … -4, -3, -2, -1, 0, +1, +2, +3, + 4…, c'est-à-dire, répertorié et organisé. Mais une représentation très utile est ce qui utilise la ligne numérique. Pour cela, il est nécessaire de tracer une ligne, qui est généralement horizontale, sur laquelle 0 est marqué et divisé en sections identiques:

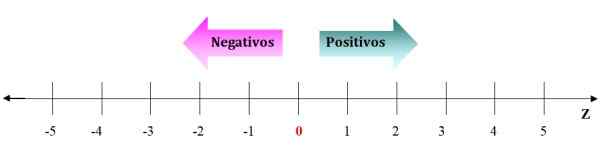Figure 2. Représentation de nombres entiers sur la ligne numérique. De 0 à la droite sont les entiers positifs et de 0 à gauche les négatifs. Source: F. Zapata.

Les négatifs vont à gauche de 0 et les positifs vont à droite. Les flèches de la ligne numérique symbolisent que les nombres continuent à l'infini. Compte tenu de tout nombre entier, il est toujours possible d'en trouver un qui est plus grand ou autre que c'est inférieur.

La valeur absolue d'un entier

La valeur absolue d'un entier est la distance entre le nombre et 0. Et les distances sont toujours positives. Par conséquent, la valeur absolue de l'entier négatif est le nombre sans son signe moins.

Par exemple, la valeur absolue de -5 est 5. La valeur absolue est indiquée avec des barres, comme suit:

| -5 | = 5

Pour le visualiser, il suffit d'avoir les espaces sur la ligne numérique, de -5 à 0. Alors que la valeur absolue d'un entier positif est le même nombre, par exemple | +3 | = 3, car sa distance à 0 est de 3 espaces:

Peut vous servir: Sandwich Loi: Explication et exercices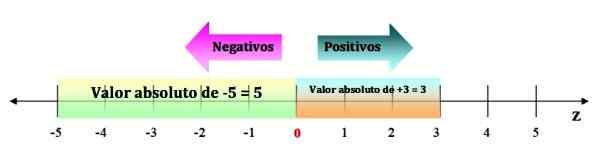figure 3. La valeur absolue d'un entier est toujours un montant positif. Source: F. Zapata.

Propriétés

-L'ensemble des nombres entiers est indiqué comme Z et comprend l'ensemble des nombres naturels n, leurs éléments étant infinis.

-Un numéro entier et celui qui suit (ou celui qui le précède) diffère toujours dans l'unité. Par exemple, après 5 sur 6, étant 1 la différence entre eux.

-Chaque nombre entier a un prédécesseur et un successeur.

-Tout entier positif est supérieur à 0.

-Un entier négatif est toujours inférieur à 0 et que tout nombre positif. Prenons par exemple le nombre -100, c'est inférieur à 2, que 10 et 50. Mais il est aussi inférieur à -10, -20 et -99 et il est supérieur à -200.

-0 n'a aucune considération de signe, car ce n'est pas négatif ou positif.

-Avec l'ensemble des nombres, les mêmes opérations qui sont effectuées avec les nombres naturels peuvent être effectuées, à savoir: somme, soustraction, multiplication, potentialisation et plus.

-L'opposé entier d'un certain entier X, est -x et la somme d'un entier avec son opposé est 0:

x + (-x) = 0.

Opérations avec des nombres entiers

- Ajout

-Si les nombres à ajouter ont le même signe, leurs valeurs absolues sont ajoutées et le résultat est placé le signe que les addeds ont. Voici quelques exemples:

a) (+8) + (+ 9) = 8 +9 = +17

b) (-12) + (- 10) = - (12 + 10) = -22

-Dans le cas où les nombres sont du signe différent, les valeurs absolues (la majeure du mineur) sont soustraites et le résultat est placé le signe du nombre avec la valeur absolue la plus élevée, comme suit:

a) (-8) + (21) = 21 - 8 = 13

b) (-9) + (+4) = - (9-4) = -5

Propriétés de la somme des nombres entiers

-La somme est commutative, donc l'ordre des addeds ne modifie pas la somme. Soit A et B deux nombres entiers, il est accompli que A + B = B + A

-0 est l'élément neutre de la somme des nombres entiers: A + 0 = A

-Tout numéro entier ajouté avec son contraire est 0. L'opposé de + a est -a, et inversement, l'opposé de -a es + a. Par conséquent: (+ a) + (-a) = 0.

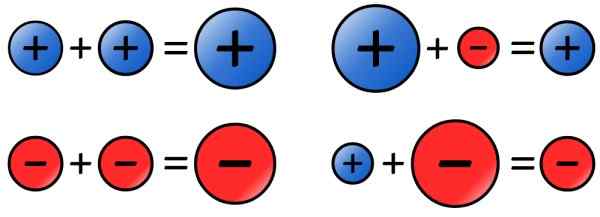Figure 4. Règle des signes pour la somme des nombres entiers. Source: Wikimedia Commons.

- Soustraction

Pour soustraire des nombres entiers, vous devez être guidé par cette règle: La soustraction équivaut à la somme d'un nombre avec son opposé. Laissez deux nombres A et B, alors:

A - b = a + (-b)

Par exemple, supposons que vous deviez effectuer l'opération suivante: (-3) - (+7), alors:

(-3) - (+ 7) = (-3) + (- 7) = - (3 + 7) = -10

- Multiplication

La multiplication des nombres entiers suit certaines règles pour les signes:

-Le produit de deux nombres avec Le même signe C'est toujours positif.

-Lorsque deux nombres se multiplient différents signes, Le résultat est toujours négatif.

Peut vous servir: quelles sont les parties de la fraction? (Exemples)

-La valeur du produit est égale à la multiplication des valeurs absolues respectives.

Immédiatement quelques exemples qui clarifient ce qui précède:

(-5) x (+8) = -5 x 8 = -40

(-10) x (-12) = 10 x 12 = 120

(+4) x (+32) = 4 x 32 = 128

Propriétés de la multiplication des nombres entiers

-La multiplication est commutative. Être deux nombres entiers A et B, il est vrai que: A.b = b.A, qui peut également être exprimé comme:

L'ordre des facteurs ne modifie pas le produit.

-L'élément neutre de la multiplication est 1. Être à un entier, donc à.1 = 1

-Tout entier multiplié par 0 est égal à 0: A.0 = 0

Propriété distributive

La multiplication rencontre une propriété distributive en ce qui concerne la somme. Oui, A, B et C sont alors des nombres entiers:

pour.(b + c) = a.b + a.c

Puis un exemple de la façon d'appliquer cette propriété:

(-3). [(-4) + 11] = (-3).(-4) + (- 3).11 = 12 -33 = 12 + (-33) = -21

Potentialisation

-Si la base est positive, le résultat de l'opération est toujours positif.

-Lorsque la base est négative, si l'exposant est égal, le résultat est positif. Et si l'exposant est impair, le résultat est négatif.

- Division

Dans la division, les mêmes règles de signes s'appliquent à la multiplication:

-En divisant deux entiers du même signe, le résultat est toujours positif.

-Lorsque deux entiers de signes différents sont divisés, le quotient est négatif.

Par exemple:

(-12) ÷ (-4) = 3

33 ÷ (-3) = -11

Important: La division n'est pas commutative, en d'autres termes à ÷ b ≠ b ÷ a et comme toujours, la division entre 0 n'est pas autorisée.

- Potentialisation

Être un nombre entier et nous voulons l'élever à un exposant n, alors nous devons nous multiplier par lui-même, comme indiqué ci-dessous:

pourⁿ = A.pour.pour.pour.… pour

Considérons également ce qui suit, en tenant compte du fait que N est un nombre naturel:

-Si A est négatif et n est même, le résultat est positif.

-Lorsque A est négatif et que n est impair, il se traduit par un nombre négatif.

-Si A est positif et que n est uniforme ou étrange, c'est toujours un entier positif.

-Tout entier élevé à 0 est égal à 1: A⁰ = 1

-Chaque nombre élevé à 1 est égal au nombre: un¹ = A

Mettons par exemple que vous souhaitez trouver (-3)⁴ , Pour le faire se multiplier (-3) quatre fois par lui-même, comme ceci: (-3).(-3).(-3).(-3) = 81.

Un autre exemple, également avec un entier négatif est:

(-2)³ = (-2).(-2).(-2) = -8

Produit de pouvoirs de base égaux

Supposons deux pouvoirs de base égale, si nous les multiplions, nous obtenons une autre puissance avec la même base, dont l'exposant est la somme des exposants donnés:

pourⁿ ·pour^m = A^{n + m}

Ratio de poudre de base égale

En divisant les pouvoirs de la même base, le résultat est une puissance avec la même base, dont l'exposant est la soustraction des exposants donnés:

Peut vous servir: angles dans la circonférence: types, propriétés, exercices résolus

pourⁿ ÷ a^m = A^{n - m}

Puis deux exemples qui clarifient ces points:

(-2)³.(-2)⁵ = (-2) ^{3 + 5}= (-2)⁸

5⁶ ÷ 5⁴ = 5^6-4 = 5²

Exemples

Regardons des exemples simples pour appliquer ces règles, en vous rappelant que dans le cas des entiers positifs, le panneau peut être distribué:

a) (+6) + (+14) = 6 + 14 = 20

b) (-8) + (- 10) = - (8 + 10) = -18

c) (-16) + (+7) = -16 + 7 = -9

d) (+4) + (-8) + (-25) = [(+4) + (-8)] + (-25) = [4-8] -25 = -4 -25 = -29

e) (-8) - (+ 15) = (-8) + (-15) = -8 -15 = -23

f) (+3) x (+9) = 3 x 9 = 27

g) (- 4) x (-11) = 4 x 11 = 44

h) (+5) x (-12) = -5 x 12 = -60

i) (-2)³ = (-2) x (-2) x (-2) = -8

Exercices résolus

- Exercice 1

Une fourmi se déplace sur la ligne numérique de la figure 1. À partir du point x = +3, les déplacements suivants:

-7 unités se déplacent vers la droite

-Maintenant, 5 unités sont retournées à gauche

-Marcher 3 unités à gauche.

-Il revient et déplace 4 unités vers la droite.

À quel moment se trouve la fourmi à la fin de l'itinéraire?

Solution

Appelons les déplacements. Quand ils sont à droite, ils ont un signe positif et lorsqu'ils sont sur le signe négatif de gauche. De cette façon, et à partir de x = +3 vous avez:

-Premier D: x₁ = +3 +7 = +10

-Deuxième D: x₂ = +10 + (- 5) = +5

-Troisième D: x₃ = +5 + (- 3) = +2

-Quatrième D: x₄ = +2 +4 = +6

Lorsque la fourmi se termine, sa marche est en position x = +6. C'est-à-dire que c'est 6 unités à droite de 0 sur la ligne numérique.

- Exercice 2

Résolvez l'opération suivante:

36 + [- (-4 + (-5) - 7)].- [- 6 + 5- (2 + 7-9)] + 2 (-8 + 6)]

Solution

Cette opération contient des signes de regroupement, qui sont des parenthèses, des crochets et des clés. Lors de la résolution, vous devez d'abord prendre soin des parenthèses, après les crochets et enfin les clés. En d'autres termes, vous devez travailler de l'intérieur.

Dans cet exercice, le point représente une multiplication, mais dans le cas où entre un nombre et une parenthèse ou un autre symbole, il n'y a aucun moment, de la même manière qu'il est compris qu'il s'agit d'un produit.

Ensuite, la résolution pas à pas, les couleurs servent de guide pour suivre le résultat de la réduction des parenthèses, qui sont les symboles de groupe les plus internes:

36 + [- (-4 + (-5) - 7)].- [- 6 + 5- (2 + 7-9)] + 2 (-8 + 6)] =

= 36 + [- (-16)].- [- 6+ 5- (0)] + 2 (-2)] =

= 36 + [16].- [- 1] -4] =

= 52.1- 4] = 52.-3 = -156

- Exercice 3

Résoudre l'équation du premier degré:

12 + x = 30 + 3x

Solution

Les termes sont regroupés avec l'inconnu à gauche de l'égalité, et les termes numériques à droite:

x - 3x = 30 - 12

- 2x = 18

X = 18 / (-2)

x = - 9