Marque de classe

Qu'est-ce qu'une marque de classe?

La Marque de classe, Également connu sous le nom de point médian, c'est la valeur qui se trouve au centre d'une classe, qui représente toutes les valeurs qui se trouvent dans cette catégorie. Fondamentalement, la marque de classe est utilisée pour le calcul de certains paramètres, tels que la moyenne arithmétique ou l'écart type.

Ensuite, la marque de classe est le milieu de tout intervalle. Cette valeur est également très utile pour trouver la variance d'un ensemble de données déjà regroupé en Clas.

Distribution de fréquence

Pour comprendre ce que la marque de classe est nécessaire, le concept de distribution de fréquence. Compte tenu d'un ensemble de données, une distribution de fréquence est un tableau qui divise ces données en un certain nombre de catégories appelées classes.

Ce tableau montre quelle est la quantité d'éléments qui appartiennent à chaque classe; Ce dernier est connu comme fréquence.

Dans ce tableau, une partie des informations que nous obtenons à partir des données est sacrifiée, car au lieu d'avoir la valeur individuelle de chaque élément, nous savons seulement qu'elle appartient à cette classe.

D'un autre côté, nous avons une meilleure compréhension de l'ensemble de données, car de cette manière, il est plus facile d'apprécier les modèles établis, ce qui facilite la manipulation desdites données.

Combien de cours considèrent?

Pour faire une distribution de fréquence, nous devons d'abord déterminer le nombre de classes que vous souhaitez suivre et choisir les limites de classe.

Peut vous servir: bords d'un cube

Le choix du nombre de cours suivis devrait être pratique, en tenant compte qu'un petit nombre de classes peuvent masquer des informations sur les données que nous voulons étudier et une très grande peut générer trop de détails qui ne sont pas nécessairement utiles.

Les facteurs que nous devons prendre en compte lors du choix du nombre de classes sont plusieurs, mais entre ces deux: la première consiste à prendre en compte le nombre de données que nous devons considérer; La seconde consiste à savoir quelle taille est la gamme de distribution (c'est-à-dire la différence entre la plus grande et la plus petite observation).

Après avoir eu les classes déjà définies, nous procédons pour compter le nombre de données dans chaque classe. Ce nombre est appelé fréquence de classe et est indiqué par correctif.

Comme nous l'avions déjà dit, nous avons une distribution de fréquence perd les informations qui proviennent individuellement de chaque données ou observation. Par conséquent, une valeur est recherchée qui représente toute la classe à laquelle il appartient; Cette valeur est le Classmark.

Comment est-il obtenu?

La marque de classe est la valeur centrale qui représente une classe. Il est obtenu en ajoutant les limites de l'intervalle et en divisant cette valeur par deux. Nous pourrions exprimer cela mathématiquement comme suit:

X_Toi= (Limite inférieure + limite supérieure) / 2.

Dans cette expression x_Toi Désigne la marque de la classe I-cette classe.

Exemple

Compte tenu de l'ensemble de données suivant, donnez une distribution de fréquence représentative et obtenez la marque de classe correspondante.

Comme les données avec la valeur numérique la plus élevée sont de 391 et que l'enfant est 221, nous avons que la plage est de 391 -221 = 170.

Peut vous servir: probabilité théorique: comment le sortir, exemples, exercices

Nous choisirons 5 classes, toutes avec la même taille. Une façon de choisir les classes est la suivante:

Notez que chaque données est dans une classe, celles-ci sont disjointes et ont la même valeur. Une autre façon de choisir des classes consiste à considérer les données dans le cadre d'une variable continue, qui pourrait atteindre n'importe quelle valeur réelle. Dans ce cas, nous pouvons considérer les classes de la forme:

205-245, 245-285, 285-325, 325-365, 365-405

Cependant, cette façon de regrouper les données peut présenter certaines ambiguïtés avec les frontières. Par exemple, dans le cas de 245, la question se pose: à quelle classe appartient-elle, au premier ou au second?

Pour éviter cette confusion, une convention de points extrêmes est faite. De cette façon, la première classe sera l'intervalle (205 245], le second (245 285], etc.

Une fois les classes définies, nous procédons à calculer la fréquence et nous avons le tableau suivant:

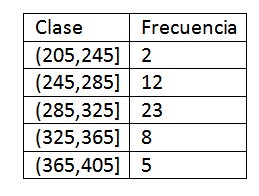
Après avoir obtenu la distribution de fréquence des données, nous trouvons les marques de classe de chaque intervalle. En effet, nous devons:

X₁= (205+ 245) / 2 = 225

X₂= (245+ 285) / 2 = 265          

X₃= (285+ 325) / 2 = 305

X₄= (325+ 365) / 2 = 345

X₅= (365+ 405) / 2 = 385

Nous pouvons représenter cela via le graphique suivant:

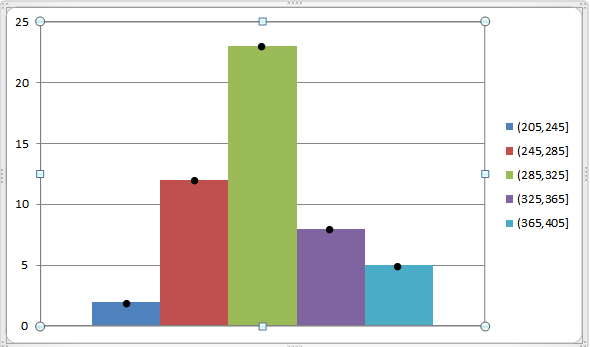
Pourquoi est-ce?

La marque de classe est très fonctionnelle pour trouver la moyenne arithmétique et la variance d'un groupe de données qui ont déjà été regroupées en différentes classes.

Nous pouvons définir la moyenne arithmétique comme la somme des observations obtenues entre la taille de l'échantillon. D'un point de vue physique, son interprétation est comme le point d'équilibre d'un ensemble de données.

L'identification d'un ensemble complet de données par un seul nombre peut être risqué, vous devez donc également prendre en compte la différence entre ce point d'équilibre et les données réelles. Ces valeurs sont connues sous le nom de déviation par rapport à la moyenne arithmétique, et avec celles-ci, il est cherché à déterminer dans quelle mesure la moyenne arithmétique des données varie.

Peut vous servir: fractions: types, exemples, exercices résolus

La façon la plus courante de trouver cette valeur est due à la variance, qui est la moyenne des carrés des écarts de la moyenne arithmétique.

Pour calculer la moyenne arithmétique et la variance d'un ensemble de données regroupées dans une classe, nous utilisons respectivement les formules suivantes:

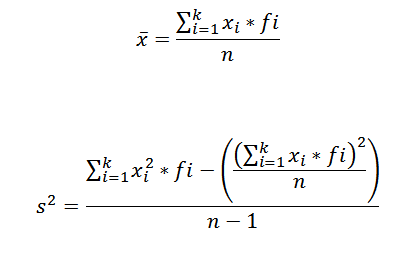
Dans ces expressions x_Toi  C'est la marque I-cette classe, f_Toi représente la fréquence correspondante et k le nombre de classes dans lesquelles les données ont été regroupées.

Exemple

En utilisant les données fournies dans l'exemple précédent, nous devons étendre un peu plus les données dans le tableau de distribution de fréquence. Les éléments suivants sont obtenus:

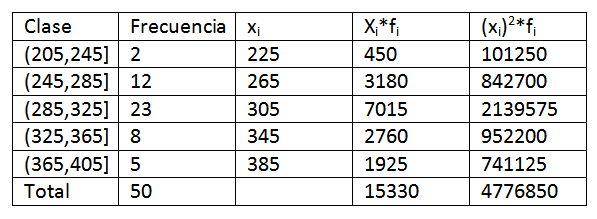
Ensuite, en remplaçant les données de la formule, nous avons laissé que la moyenne arithmétique est:

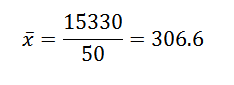
Sa variance et son écart-type sont:

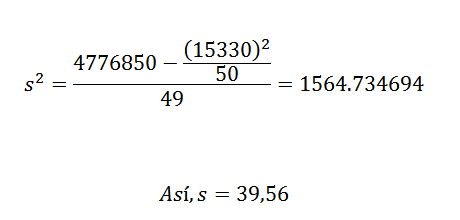
À partir de cela, nous pouvons conclure que les données d'origine ont une moyenne arithmétique de 306,6 et un écart-type de 39,56.