Modèle atomique bohr

Il Modèle atomique bohr C'est la conception du physicien danois Niels Bohr (1885-1962) sur la structure de l'atome, publiée en 1913. Dans l'atome de Bohr, les électrons autour du noyau n'occupent que certaines orbites autorisées, grâce à une restriction appelée quantification.

Pour Bohr, l'image de l'atome en tant que système solaire miniature, avec des électrons en orbite autour du noyau, il n'était pas entièrement cohérent avec le fait que les charges électriques, lorsqu'elles sont accélérées, rayonnent d'énergie.

Un atome comme celui-là ne serait pas stable, car il finirait de s'effondrer tôt ou tard parce que les électrons se précipiteraient en spirale vers le noyau. Et d'ici là, il y a 50 ans, les modèles de lumière caractéristiques qui émettent de l'hydrogène et d'autres gaz lors du chauffage.

Le motif ou le spectre se compose d'une série de lignes lumineuses de certaines longueurs d'onde très spécifiques. Et l'atome d'hydrogène ne s'effondre pas en émettant de la lumière.

Pour expliquer pourquoi l'atome est stable malgré la possibilité de rayonner de l'énergie électromagnétique, Bohr a proposé que le moment angulaire ne puisse adopter que certaines valeurs, et donc l'énergie aussi. C'est ce qui est compris par la quantification.

Acceptant que l'énergie a été quantifiée, l'électron aurait la stabilité nécessaire à ne pas se précipiter vers le noyau détruisant l'atome.

Et l'atome ne fait que rayon d'énergie lumineuse lorsque l'électron fait des transitions d'une orbite à une autre, toujours en quantités discrètes. De cette façon, la présence de schémas d'émission dans l'hydrogène est expliquée.

Bohr a composé de cette manière une vision de l'atome intégrant les concepts connus de mécanique classique avec le nouvellement découvert, comme la constante de Planck, le photon, l'électron, le noyau atomique (Rutherford avait été un mentor de Bohr) et le spectre de problème susmentionné et susmentionné.

[TOC]

Caractéristiques principales du modèle Bohr

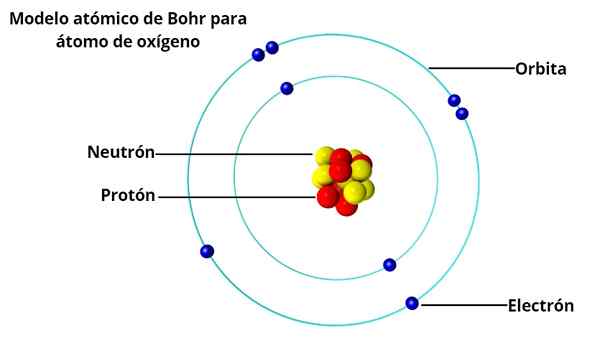
Bohr's Atome. L'animation représente l'électron lorsqu'il passe d'un niveau d'énergie supérieur à un autre d'énergie moins, émettant une lumière de lumière (un photon). Source: Wikimedia Commons.

Le modèle atomique de Bohr suppose que l'électron se déplace dans une orbite circulaire autour du noyau par l'action de l'attraction électrostatique de Coulomb et propose que le moment angulaire de l'électron soit quantifié.

Peut vous servir: équilibrage vecteur: calcul, exemples, exercices

Voyons comment intégrer les deux concepts sous forme mathématique:

Soit l l'ampleur du moment angulaire, m la masse de l'électron et la vitesse de l'électron et r le rayon de l'orbite. Pour calculer l, nous avons:

L = m⋅r⋅v

Bohr a proposé que L était égal à des multiples entiers de la constante H / 2π, où H est le Constante de Planck, introduit il y a peu de temps par le physicien Max Planck (1858-1947) pour résoudre le problème énergétique émis par un corps noir, un objet théorique qui absorbe toute la lumière incidente.

Sa valeur est h = 6.626 × 10⁻³⁴ J ・ s, tandis qu'à h / 2π, il est désigné comme ħ, Qui lit  "H Bar".

Par conséquent, le moment angulaire L reste:

m⋅r⋅v = nħ, Avec n = 1,2, 3 ..

Et à partir de cette condition, les radios des orbites autorisées pour l'électron sont déduites, comme nous le verrons alors.

Calcul du rayon d'orbite électronique

Dans ce qui suit, nous supposerons le plus simple des atomes: l'hydrogène, qui se compose d'un seul proton et d'un électron, à la fois avec une charge de magnitude et.

La force centripète qui maintient l'électron dans son orbite circulaire est fournie par l'attraction électrostatique, dont l'amplitude f est:

F = ke²/ r²

Où k est la constante électrostatique de la loi Coulomb et R la distance électronique-protéine. Sachant que dans un mouvement circulaire, l'accélération centripète_c Il est donné par raison entre le carré de vitesse et la distance R:

pour_c = V² / r

Par la deuxième loi de Newton, la force nette est le produit de la masse M par accélération:

Mv²/ r = ke²/ r²

La simplification de la radio R est obtenue:

M⋅v²R = ke²

Combinant cette expression avec celle du moment angulaire, nous avons un système d'équations, donné par:

Il peut vous servir: trajectoire physique: caractéristiques, types, exemples et exercices

1) MV²R = ke²

2) r = n ħ/ mv

L'idée est de résoudre le système et de déterminer R, le rayon de l'orbite autorisée. Une petite algèbre élémentaire mène à la réponse:

R = (nħ)² / K⋅m⋅e²

Avec n = 1, 2, 3, 4, 5 ..

Pour n = 1, nous avons le moindre des radios, appelé Bohr Radio A_soit Avec une valeur de 0,529 × 10⁻¹⁰ m. Les radios des autres orbites sont exprimées en termes de pour_soit.

De cette façon, Bohr présente le principal numéro quantique n, soulignant que les radios autorisées sont basées sur la constante de Planck, la constante électrostatique et la masse et la charge de l'électron.

Le modèle atomique Bohr postule

Le physicien danois Niels Bohr (1885-1962).

Bohr combine habilement la mécanique newtonienne avec les nouvelles découvertes qui avaient permis de manière continue au cours de la seconde moitié du 19e siècle et du début du 20e siècle. Parmi eux le concept révolutionnaire de «combien», dont Planck lui-même prétendait ne pas être très convaincu.

Grâce à sa théorie, Bohr pourrait expliquer de manière satisfaisante la série du spectre d'hydrogène et prédire les émissions d'énergie dans le rang de l'ultraviolet et de l'infrarouge, qui n'avait pas encore été observé.

Nous pouvons résumer vos postulats comme suit:

Les électrons décrivent les trajectoires circulaires

L'électron tourne autour du noyau en orbite circulaire stable, avec un mouvement circulaire uniforme. Le mouvement est dû à l'attraction électrostatique que le noyau exerce dessus.

Le moment angulaire est quantifié

Le moment angulaire de l'électron est quantifié en fonction de l'expression:

L = mvr = nħ

Où n est un entier: n = 1, 2, 3, 4 ..., ce qui conduit à l'électron ne peut être que dans certaines orbites définies, dont les radios sont:

R = (n ħ)² / k m e²

Les électrons émettent ou absorbent des photons lorsqu'ils passent d'un état d'énergie à un autre

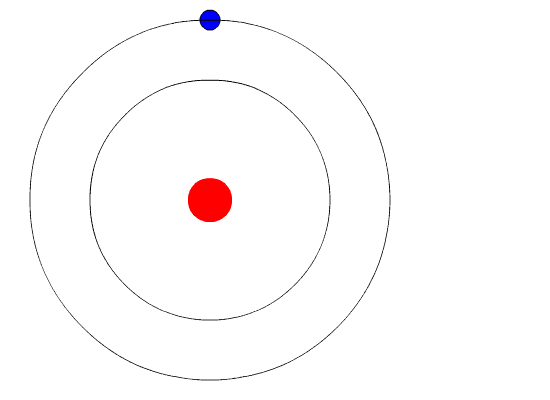
Lors du passage d'un état d'énergie à un autre, l'électron absorbe ou émet de l'énergie en quantités discrètes appelées photons. Source: Wikimedia Commons.

Étant donné que le moment angulaire est quantifié, énergie et aussi. Il peut être démontré que E est donné par:

Peut vous servir: tir vertical: formules, équations, exemples

Et remplacer toutes les constantes, une forme abrégée est obtenue:

L'électron Volt ou EV est une autre unité d'énergie, largement utilisée en physique atomique. Le signe négatif de l'énergie assure la stabilité de l'orbite, indiquant que le travail doit être effectué pour séparer l'électron de cette position.

Tandis que l'électron est dans son orbite n'absorbe pas ou n'émet pas de lumière. Mais quand il saute d'une orbite de plus grande énergie à une plus faible, elle fait.

La fréquence F de la lumière émise dépend de la différence entre les niveaux d'énergie des orbites:

E = hf = e_initial - e_final

Limites

Le modèle Bohr a certaines limites:

-Il ne s'applique qu'à l'atome d'hydrogène. Les tentatives de l'appliquer à des atomes plus complexes n'ont pas fonctionné.

-Il ne répond pas pourquoi certaines orbites sont stables et d'autres non. Le fait que l'énergie dans l'atome ait été quantifiée a très bien fonctionné, mais le modèle n'a pas fourni de raison, et c'était quelque chose qui a provoqué l'inconfort aux scientifiques.

-Une autre limitation importante est qu'elle n'a pas expliqué les lignes supplémentaires émises par les atomes en présence de champs électromagnétiques (effet Zeeman et effet brut). Ou pourquoi certaines lignes de spectre étaient plus intenses que d'autres.

-Le modèle Bohr ne considère pas les effets relativistes, ce qui est nécessaire.

-Il faut pour acquis qu'il est possible de connaître précisément la position et la vitesse de l'électron, mais ce qui est vraiment calculé, c'est la probabilité que l'électron occupe une certaine position.

Malgré ses limites, le modèle a connu un grand succès à l'époque, non seulement pour intégrer de nouvelles découvertes à des éléments déjà connus, mais parce qu'il montrait de nouvelles questions, indiquant clairement que le chemin vers une explication satisfaisante de l'atome était en mécanique quantique.

Articles d'intérêt

Modèle atomique Schrödinger.

Modèle atomique broglie.

Modèle atomique de Chadwick.

Modèle atomique Heisenberg.

Modèle atomique perrin.

Modèle atomique Thomson.

Modèle atomique de Dalton.

Modèle atomique de Dirac Jordan.

Modèle atomique démocrite.

Modèle atomique de leucipo.

Modèle atomique Sommerfeld.

Modèle atomique actuel.