Définition de masse atomique, types, comment le calculer, exemples

La masse atomique C'est la quantité de matière présente dans un atome, qui peut être exprimée en unités physiques ordinaires ou dans des unités de masse atomique (Uma ou U). Un atome est vide dans presque toute sa structure; des électrons qui sont flous dans les régions appelées orbitales, où il y a une certaine probabilité de les trouver, et leur noyau.

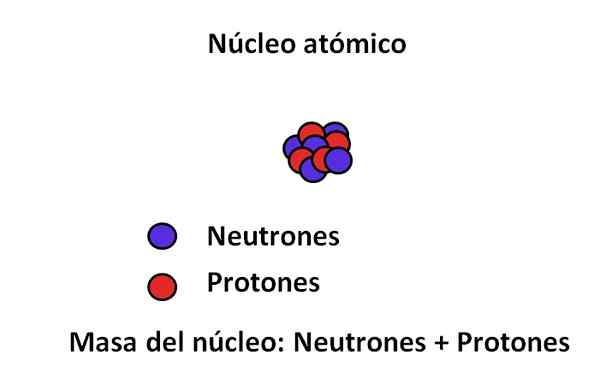
Dans le noyau de l'atome se trouvent des protons et des neutrons; Le premier avec des charges positives, tandis que les secondes avec une charge neutre. Ces deux particules subatomiques ont une masse beaucoup plus grande que celle de l'électron; Par conséquent, la masse d'un atome est régie par son noyau et non par le vide ou les électrons.

Les principales particules subatomiques et la masse du noyau. Source: Gabriel Bolívar.

La masse d'un électron est d'environ 9,1 · 10^-31 kg, tandis que le proton 1,67 · 10^-27 kg, étant le rapport de masse de 1.800; c'est-à-dire qu'un proton "pèse" 1.800 fois plus qu'un électron. De même, la même chose se produit avec les masses de neutrons et d'électrons. C'est pourquoi la contribution massive de l'électron à des fins ordinaires est considérée comme négligeable.

Pour cette raison, il est généralement supposé que la masse de l'atome, ou la masse atomique ne dépend que de la masse du noyau; qui à son tour se compose de la somme du sujet des neutrons et des protons. À partir de ce raisonnement, deux concepts émergent: le nombre de masse et la masse atomique, tous deux intimement liés.

Ayant tellement de "vide" dans les atomes, et comme sa masse est presque entièrement le noyau, il est prévu que ce dernier sera extraordinairement dense.

Si nous faisions ce vide à n'importe quel corps ou objet, ses dimensions seraient radicalement. De plus, si nous pouvions construire un petit objet basé sur des noyaux atomiques (sans électrons), cela aurait une masse de millions de tonnes.

D'un autre côté, les masses atomiques aident à distinguer différents atomes du même élément; Ce sont les isotopes. Ayant des isotopes plus abondants que d'autres, une moyenne des masses d'atome pour un certain élément doit être estimée; moyen qui peut varier de la planète sur la planète, ou d'une région spatiale à une autre.

[TOC]

Définition et concept

Par définition, la masse atomique est la somme des masses de leurs protons et neutrons exprimés par uma ou u. Le nombre résultant (également appelé numéro de masse) est placé sans dimension dans le coin supérieur gauche dans la notation utilisée pour les nucléides. Par exemple, pour l'élément ^quinzeX Sa masse atomique est 15UM ou 15U.

La masse atomique ne peut pas en dire beaucoup sur la véritable identité de cet élément x. Au lieu de cela, le nombre atomique est utilisé, ce qui correspond aux protons qui abritent le noyau de x. Si ce nombre est de 7, la différence (15-7) sera égale à 8; c'est-à-dire que x a 7 protons et 8 neutrons, dont la somme est 15.

Revenant à l'image, le noyau a 5 neutrons et 4 protons, donc son nombre de masse est de 9; Et à son tour 9, Uma est la masse de son atome. Ayant 4 protons et consultant le tableau périodique, on peut voir que ce noyau correspond à l'élément de béryllium, être (ou ⁹ÊTRE).

Unité de masse atomique

Les atomes sont trop petits pour mesurer leurs masses par des méthodes conventionnelles ou des échelles ordinaires. C'est pour cette raison que l'uma, ou o da (daltón) a été inventée. Ces unités conçues pour les atomes vous permettent d'avoir une idée de la façon dont les atomes d'un élément sont massifs.

Peut vous servir: cobalt: structure, propriétés, applications

Mais que représente exactement un uma? Il doit y avoir une référence qui vous permet d'établir des relations de masse. Pour ce faire, l'atome a été utilisé comme référence ¹²C, qui est l'isotope le plus abondant et le plus stable pour le carbone. Ayant 6 protons (leur nombre atomique Z) et 6 neutrons, sa masse atomique est donc 12.

On suppose que les protons et les neutrons ont les mêmes masses, de sorte que chaque contribution 1 uma. L'unité de masse atomique est ensuite définie comme la douze parties (1/12) de la masse A atome en carbone-12; C'est, la masse d'un proton ou d'un neutron.

Équivalence en grammes

Et maintenant, la question suivante se pose: combien de grammes équivaut à 1 uma? Comme au début, il n'y avait pas de techniques suffisamment avancées pour la mesurer, les produits chimiques devaient se contenter d'exprimer toutes les masses avec UMA; Cependant, c'était un avantage et non un inconvénient.

Parce que? Parce qu'étant les petites particules subatomiques, tout comme un enfant, ce doit être leur masse exprimée en grammes. En fait, 1 UMA équivaut à 1 6605 · 10^-24 grammes. De plus, avec l'utilisation du concept de mol, ce n'était pas un problème pour travailler les masses des éléments et leurs isotopes avec UMA sachant que ces unités pouvaient être modifiées en g / mol.

Par exemple, revenir à ^quinzeX et ⁹Soyez, nous avons que leurs masses atomiques sont respectivement de 15 uma et 9 uma,. Comme ces unités sont si petites et ne disent pas à quel point il faut "peser" la question pour les manipuler, ils se transforment en leurs masses molaires respectives: 15 g / mol et 9 g / mol (introduisant les concepts de grains de beauté et de numéro Avogadro).

Masse atomique moyenne

Tous les atomes du même élément n'ont pas la même masse. Cela signifie qu'ils doivent avoir plus de particules subatomiques dans le noyau. Étant le même élément, le nombre ou le nombre de protons atomiques doit rester constant; Par conséquent, il n'y a que une variation des quantités de neutrons qui possèdent.

Ainsi, il apparaît de la définition des isotopes: atomes du même élément mais avec différentes masses atomiques. Par exemple, le béryllium se compose presque entièrement de l'isotope ⁹Être, avec des traces de traces ^dixÊtre. Cependant, cet exemple n'aide pas beaucoup à comprendre le concept de masse atomique moyenne; Nous en avons besoin avec plus d'isotopes.

Exemple

Supposons que l'élément existe ⁸⁸J, c'est le principal isotope de J avec une abondance de 60%. J a en plus deux autres isotopes: ⁸⁶J, avec une abondance de 20%, et ⁹⁰J, avec une abondance également 20%. Cela signifie que à partir de 100 atomes J que nous collectons sur Terre, 60 d'entre eux sont ⁸⁸J, et les 40 autres un mélange de ⁸⁶J et ⁹⁰J.

Chacun des trois isotopes de J a sa propre masse atomique; c'est-à-dire sa somme de neutrons et de protons. Cependant, ces masses doivent être moyennées pour pouvoir avoir une masse atomique pour J; ici sur terre, car il peut y avoir d'autres régions de l'univers où l'abondance de ⁸⁶J est 56% et pas 60%.

Peut vous servir: sodium: histoire, structure, propriétés, risques et utilisations

Pour calculer la masse atomique moyenne de J, la moyenne pondérée des masses de leurs isotopes doit être obtenue; c'est-à-dire en tenant compte du pourcentage d'abondance pour chacun d'eux. Ainsi nous avons:

Masse moyenne (J) = (86 UMA) (0,60) + (88 UMA) (0,20) + (90 UMA) (0,20)

= 87,2 Uma

C'est-à-dire que la masse atomique moyenne (également connue sous le nom de J est 87,2 UMA. Pendant ce temps, sa masse molaire est de 87,2 g / mol. Notez que 87.2 est proche de 88 que 86 et est également éloigné de 90.

Masse atomique absolue

La masse atomique absolue est la masse atomique exprimée en grammes. À partir de l'exemple de l'élément hypothétique, nous pouvons calculer sa masse atomique absolue (la moyenne) sachant que chaque UMA équivaut à 16605 · 10^-24 Grams:

Masse atomique absolue (J) = 87,2 Uma * (1 6605 · 10^-24 g / uma)

= 1,447956 · 10^-22 G / Atom J

Cela signifie qu'en moyenne, les atomes J ont une masse absolue de 1,447956 · 10^-22 g.

Masse atomique relative

La masse atomique relative est identique à la masse atomique moyenne pour un élément donné; Cependant, contrairement à la seconde, la première manque d'unité. Par conséquent, c'est sans dimension. Par exemple, la masse atomique moyenne de béryllium est de 9 012182 U; Alors que sa masse atomique relative est simplement 9 012182.

C'est pourquoi parfois ces concepts sont généralement mal compris comme des synonymes, car ils sont très similaires et les différences entre elles sont subtiles. Mais quels sont ces masses relatives? Par rapport aux douze parties de la masse du ¹²C.

Ainsi, un élément avec une masse atomique relative de 77 signifie qu'il a une masse 77 fois supérieure à 1/12 partie du ¹²C.

Ceux qui ont gagné les éléments dans le tableau périodique peuvent voir que leurs masses s'expriment relativement. Ils n'ont pas d'unités UMA, et elle est interprétée comme: le fer a une masse atomique de 55 846, ce qui signifie qu'il est 55 846 fois plus massif que la masse de 1/12 partie de la partie de la partie du ¹²C, et qui peut également être exprimé comme 55 846 UMA ou 55 846 g / mol.

Comment calculer la masse atomique

Mathématiquement un exemple de la façon de le calculer avec l'exemple de l'élément J. En termes généraux, la formule moyenne pondérée doit être appliquée, ce qui serait:

P = σ (masse atomique isotopique) (abondance dans les décimales)

En d'autres termes, avoir les masses atomiques (neutrons + protons) de chaque isotope (naturel ordinaire) pour un certain élément, ainsi que leurs abondances terrestres respectives (ou quelle que soit la région considérée), alors ladite moyenne pondérée peut être calculée.

Et pourquoi pas simplement la moyenne arithmétique? Par exemple, la masse atomique moyenne de J est de 87,2 UMA. Si nous calculons à nouveau cette masse mais d'une manière arithmétique, nous aurons:

Masse moyenne (j) = (88 uma + 86 uma + 90 uma) / 3

= 88 Uma

Notez qu'il existe une différence importante entre 88 et 87.2. En effet, dans la moyenne arithmétique, on suppose que l'abondance de tous les isotopes est la même; Lorsqu'il y a trois isotopes J, chacun doit avoir une abondance de 100/3 (33,33%). Mais ce n'est pas vraiment: il y a des isotopes beaucoup plus abondants qu'un autre.

Il peut vous servir: uréthane: structure, propriétés, obtention, utilisations

C'est pourquoi la moyenne pondérée est calculée, car il est pris en considération à quel point un isotope est abondant par rapport à un autre.

Exemples

Carbone

Pour calculer la masse atomique moyenne de carbone, nous avons besoin de ses isotopes naturels avec leurs abondances respectives. Dans le cas du carbone, ce sont: ¹²C (98,89%) et ¹³C (1,11%). Les masses atomiques relatives d'entre elles sont respectivement de 12 et 13, qui à leur tour sont égales à 12 uma et 13 uma. Solving:

Masse atomique moyenne (C) = (12 UMA) (0,9889) + (13 UMA) (0,0111)

= 12 0111 Uma

Par conséquent, la masse d'un atome de carbone est en moyenne 12,01 UMA. Avoir des traces de traces de ¹⁴C, il n'a presque aucune influence sur cette moyenne.

Sodium

Tous les atomes de sodium terrestre sont constitués de l'isotope ²³Na, donc son abondance est à 100%. C'est pourquoi dans les calculs ordinaires, on peut supposer que sa masse est simplement 23 Uma ou 23 g / mol. Cependant, sa masse exacte est de 22.98976928 Uma.

Oxygène

Les trois isotopes d'oxygène avec leurs abondances respectives sont: ¹⁶O (99 762%), ¹⁷Ou (0,038%) et ¹⁸O (0,2%). Nous avons tout pour calculer sa masse atomique moyenne:

Masse atomique moyenne (O) = (16 UMA) (0,99762) + (17 UMA) (0,00038) + (18 UMA) (0,002)

= 16,00438 Uma

Bien que sa masse exacte signalée soit en fait de 15 9994 UMA.

Azote

Répéter les mêmes étapes avec l'oxygène que nous avons: ¹⁴N (99 634%) et ^quinzeN (0,366%). Ensuite:

Masse atomique moyenne (n) = (14 UMA) (0,99634) + (15 UMA) (0,00366)

= 14,00366 Uma

Notez que la masse rapportée pour l'azote est de 14 0067 UMA, un peu plus grande que ce que nous calculons.

Chlore

Les isotopes du chlore avec leurs abondances respectives sont: ³⁵Cl (75,77%) et ³⁷CL (24,23%). Calcul de sa masse atomique moyenne que nous avons:

Masse atomique moyenne (CL) = (35 UMA) (0,7577) + (37 UMA) (0,2423)

= 35 4846 uma

Très similaire au rapport (35 453 UMA).

Dissosio

Et enfin, la masse moyenne d'un élément avec de nombreux isotopes naturels sera calculé: Disposio. Ceux-ci et avec leurs abondances respectives sont: ¹⁵⁶Dy (0,06%), ¹⁵⁸Dy (0,10%), ¹⁶⁰Dy (2,34%), ¹⁶¹Dy (18,91%), ¹⁶²Dy (25,51%), ¹⁶³Dy (24,90%) et ¹⁶⁴Dy (28,18%).

Nous procédons comme les exemples précédents pour calculer la masse atomique de ce métal:

Masse atomique moyenne (DY) = (156 UMA) (0,0006%) + (158 UMA) (0,0010) + (160 UMA) (0,0234) + (161 UMA) (0,1891) + (162 UMA) (0,2551) + (163 Uma) (0,2490) + (164 Uma) (0,2818)

= 162 5691 Uma

La masse signalée est de 162 500 uma. Notez que cette moyenne se situe entre 162 et 163, car les isotopes ¹⁵⁶Dy, ¹⁵⁸Dy et ¹⁶⁰Dy sont peu abondants; tandis que ceux qui prédominent sont ¹⁶²Dy, ¹⁶³Dy et ¹⁶⁴Dy.

Les références

1. Whitten, Davis, Peck & Stanley. (2008). Chimie. (8e Ed.). Cengage Learning.
2. Wikipédia. (2019). Masse atomique. Récupéré de: dans.Wikipédia.org
3. Christopher Masi. (s.F.). Masse atomique. Récupéré de: wsc.Masse.Édu
4. Natalie Wolchover. (12 septembre 2017). Comment pondér-tu un atome? Science en direct. Récupéré de: LiveScience.com
5. CHIMISTER BOOLISTexts. (5 juin 2019). Calculer les masses atomiques. Récupéré de: Chem.Bibliothèque.orks
6. Edward Wichers et H. Steffen Peiser. (15 décembre 2017). Poids atomique. Encyclopædia Britannica. Récupéré de: Britannica.com