FERMAT limite ce qui consiste et les exercices résolus

Il Limite de fermat Il s'agit d'une méthode numérique utilisée pour atteindre la valeur de la pente d'une ligne, qui est tangente à une fonction spécifique de son domaine. Il est également utilisé pour obtenir des points critiques d'une fonction. Son expression est définie comme:

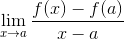
Il est évident que Fermat ne connaissait pas les fondements de la dérivation, mais ce sont ses études qui ont favorisé un groupe de mathématiciens pour se renseigner sur les lignes tangentes et leurs applications dans le calcul.

[TOC]

Quelle est la limite de Fermat?

Il se compose d'une approche de 2 points qui, dans les conditions précédentes, forment une ligne sécante à la fonction avec l'intersection par paires de valeurs.

Lorsque vous approchez de la variable à la valeur «A», la paire de points est obligé de répondre. De cette façon, la ligne de séchage précédemment devient tangente au point (a; f (a)).

La valeur quotient (x - a), lorsqu'elle est évaluée au point «A», jette une indétermination des limites de type K entre zéro (k / 0). Où ces indéterminations peuvent être brisées à travers différentes techniques de factorisation.

Les techniques de fonctionnement les plus utilisées sont:

-Différence carrée (un² - b² ) = (a + b) (a - b); L'existence de l'élément (A-B) implique dans une grande partie des cas le facteur qui simplifie l'expression (X-A) dans le rapport limite Fermat.

- Achèvement carré (hache² + bx); Après avoir terminé les carrés, un binôme de Newton est obtenu, où l'un de ses 2 facteurs est simplifié avec l'expression (x - a), brisant l'indétermination.

- Conjugué (a + b) / (a ​​+ b); Multiplier et diviser l'expression par le conjugué d'un facteur peut être d'une grande aide pour briser l'indétermination.

- Facteur commun; Dans de nombreux cas, le résultat de l'exploitation du numérateur du Fermat F (x) - F (a) caché au facteur (x - a) nécessaire pour factoriser. Pour cela, on observe attentivement quels éléments sont répétés dans chaque facteur de l'expression.

Fermat Limit Application pour maximum et minimum

Même lorsque la limite de Fermat ne fait pas la différence entre maximum et minimum.

Les connaissances de base sur la théorie graphique des fonctions en conusité avec ce théorème peuvent être suffisantes pour établir des valeurs maximales et minimales entre les fonctions. En fait, les points d'inflexion peuvent être définis par le théorème de la valeur moyenne supplémentaire au théorème de Fermat.

La parabole cubique

Le paradoxe le plus important pour Fermat est venu lors de l'étude de la parabole cubique. Parce que son attention visait les lignes tangentes d'une fonction pour un point donné, il a rencontré le problème de définir cette ligne tangente au point d'inflexion existant dans la fonction.

Il semblait impossible de déterminer la ligne tangente à un point. Commence ainsi l'enquête qui donnerait naissance au calcul différentiel. Puis défini par des exposants importants de mathématiques.

Maximus et minimaux

L'étude du maximum et du minimum d'une fonction a été un défi pour les mathématiques classiques, où une méthode sans équivoque et pratique pour la définition de ces.

Fermat a créé une méthode basée sur le fonctionnement de petites valeurs différentielles, qui après les processus de factorisation sont éliminées en cédant la place à la valeur la plus et minimale.

Cette variable doit être évaluée dans l'expression d'origine pour déterminer la coordonnée dudit point, qui avec les critères analytiques sera défini par le maximum ou le minimum de l'expression.

Méthode

Dans sa méthode, Fermat utilise le symbolisme littéral de Vieta, qui consistait en l'utilisation exclusive de majuscules: les voyelles, pour les inconnues et les consonnes pour les quantités connues.

Dans le cas de valeurs radicales, Fermat a mis en œuvre un processus particulier, qui serait plus tard utilisé dans les factorisations des limites d'indétermination Infinity entre l'infini.

Ce processus consiste à diviser chaque expression par la valeur différentielle utilisée. Dans le cas de Fermat, a utilisé la lettre E, où après la division entre le plus grand pouvoir de E, la valeur demandée sur le point critique devient clair.

Histoire

La limite de Fermat est en fait l'une des contributions les moins renommées de la longue liste des mathématiciens. Ses études provenaient de nombres premiers, pour créer essentiellement les bases de calcul.

À son tour, Fermat était connu pour ses excentricités concernant ses hypothèses. C'était courant pour une sorte de défi aux autres mathématiciens de l'époque, alors qu'il avait déjà la solution ou la démonstration.

Il y avait une grande variété de litiges et d'alliances avec différents mathématiciens de l'époque, qui aimaient ou détestent travailler avec lui.

Son dernier théorème était le principal responsable de sa renommée mondiale, où il a dit qu'une généralisation de la théorème de Pythagore Pour tout degré "N", c'était impossible. Dit en avoir une démonstration valable, mais est décédé avant de le rendre public.

Cette manifestation a dû attendre environ 350 ans. En 1995, les mathématiciens Andrew Wiles et Richard Taylor ont mis fin à l'anxiété laissée par Fermat, démontrant qu'il était juste à travers une démonstration valable de son dernier théorème.

Exercices

Exercice 1

Définissez la pente de la ligne tangente à la courbe f (x) = x² Au point (4, 16)

Remplacement dans l'expression de la limite Fermat que vous avez:

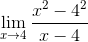
Puis en appliquant des minimums carrés, le numérateur est un facteur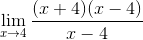

Les facteurs sont simplifiés (x - 4)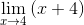

Lors de l'évaluation, vous avez

M = 4 + 4 = 8

Exercice 2

Définir le point d'expression critique f (x) = x² + 4x en utilisant la limite Fermat

Dans ce cas, il n'y a pas de coordonnée, donc la valeur x est remplacée par la forme générique x₀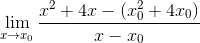

Un regroupement stratégique d'éléments est effectué, cherchant à regrouper les pairs X-X₀

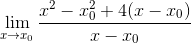
Les carrés sont développés

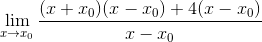
Le facteur commun X-X est observé_{0 et est extrait}

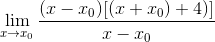
L'expression peut déjà être simplifiée et l'indétermination est brisée

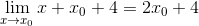
Dans les points minimaux, il est connu que la pente de la ligne tangente est égale à zéro. De cette façon, nous pouvons correspondre à zéro l'expression trouvée et effacer la valeur x₀    

2 x₀ + 4 = 0

X₀ = -4/2 = -2

Pour obtenir la coordonnée manquante, vous n'avez qu'à évaluer le point de la fonction d'origine

F (-2) = (-2)² + 4 (-2) = 4 - 8 = - 4

Le point critique est P (-2, -4).

Les références

1. Analyse réelle. Une approche historique Sauhl Stahl, John Wiley & Sons, 5 août. 1999.
2. La carrière mathématique de Pierre par Fermat, 1601-1665: deuxième édition. Michael Sean Mahoney. Princeton University Press, 5 juin. 2018
3. De Fermat à Minkowski: conférences sur la théorie des nombres et son développement historique. W. Scharlau, h. Opolka, Springer Science & Business Media, 1985
4. Dernier théorème de Fermat: une introduction génétique à la théorie des nombres algébriques. Harold M. Edwards. Springer Science & Business Media, 14 janvier. 2000
5. Fermat Days 85: Mathématiques pour l'optimisation. J.-B. Hiriart-Uruty Elsevier, 1er janvier. 1986