Explication des lois Kepler, exercices, expérience

Le Lois Kepler À propos du mouvement planétaire a été formulé par l'astronome allemand Johannes Kepler (1571-1630). Kepler les a déduits sur la base du travail de son professeur astronome danois Tycho Brahe (1546-1601).

Brahe a soigneusement compilé les données des mouvements planétaires sur plus de 20 ans, avec une précision et une précision surprenantes, s'il est pris en compte qu'au moment où le télescope n'avait pas encore été inventé. La validité de vos données est toujours valable aujourd'hui.

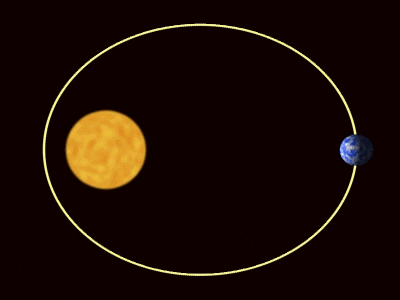Figure 1. Les orbites des planètes selon les lois de Kepler. Source: Wikimedia Commons. Willow / cc par (https: // CreenIveCommons.Org / licences / par / 3.0)

[TOC]

Les 3 lois de Kepler

Les lois de Kepler s'établissent:

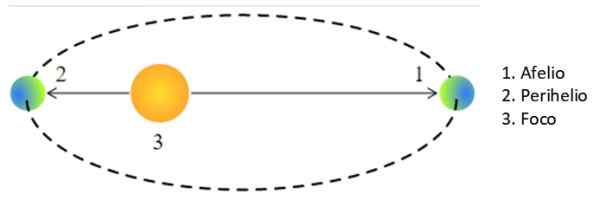
-Première loi: Toutes les planètes décrivent des orbites elliptiques avec le soleil dans l'un des projecteurs.

-Deuxième loi ou loi de la même chose: Une ligne dirigée du soleil à n'importe quelle planète (radio focale), balayez les zones égales dans les temps égaux.

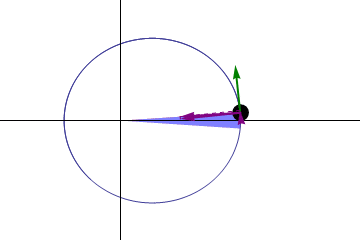Figure 2. Droit des zones. Source: Wikimedia Commons. Gonfer / cc by-sa (https: // CreativeCommons.Org / licences / by-sa / 3.0)

-Troisième loi: Le carré du temps qui prend toute planète orbitale autour du soleil est proportionnel au cube de sa distance moyenne au soleil.

Être T dit le temps, appelé Période orbitale, et r La distance moyenne, alors:

T² est proportionnel à r³

T = k r³

Cela signifie que le quotient T²/ r³ C'est la même chose pour toutes les planètes, ce qui permet de calculer le rayon orbital, si la période orbitale est connue.

Quand T Il s'exprime depuis des années et r Dans les unités astronomiques ua *, la constante de proportionnalité vaut k = 1:

T²= r³

* Une unité astronomique équivaut à 150 millions de kilomètres, ce qui est la distance moyenne entre la Terre et le Soleil. La période orbitale de la Terre est 1 an.

La loi universelle sur la gravitation et la troisième loi de Kepler

La loi universelle sur la gravitation établit que l'ampleur de la force d'attraction gravitationnelle entre deux objets de masse M et m respectivement, dont les centres sont séparés une distance r, Il est donné par:

F = g mm / r²

G est la constante de gravitation universelle et sa valeur est g = 6.674 x 10 ^-onze N.m²/kg² .

Maintenant, les orbites des planètes sont elliptiques avec une très petite excentricité.

Cela signifie que l'orbite ne s'éloigne pas beaucoup d'un cercle, sauf dans certains cas comme le nain Pluton. Si nous approximations des orbites à la forme circulaire, l'accélération du mouvement de la planète est:

pour_c = V²/ r

Étant donné que F = MA, ont:

G MM / R² = m.V²/ r

Ici V C'est la vitesse linéaire de la planète autour du soleil, de l'hypothèse statique et de masse M, Alors que la planète est m. Ensuite:

Peut vous servir: chiffres significatifs: règles, exemples, exercices résolus

Cela explique que les planètes les plus éloignées du soleil ont une vitesse orbitale inférieure, car cela dépend de 1 / √r.

Comme la distance que la planète voyage est approximativement la longueur de la circonférence: l = 2πr et il faut un temps égal t, la période orbitale, elle est obtenue:

V = 2πr / t

L'égalisation des deux expressions pour v une expression valide pour t est obtenue², Le carré de la période orbitale:

Et c'est précisément la troisième loi de Kepler, car dans cette expression la parenthèse 4π² / GM C'est constant, donc T² est proportionnel à la distance r surélevé au cube.

L'équation définitive de la période orbitale est obtenue en extraitant la racine carrée:

Calcul de la masse du soleil

Combien coûte la masse du soleil? Il est possible de le découvrir à travers cette équation. Nous savons que la période orbitale de la Terre est d'un an et que le rayon orbital est de 1 UA, équivalent à 150 millions de kilomètres, nous avons donc toutes les données nécessaires.

Dans notre équation précédente, nous effacons M, mais pas avant de convertir toutes les valeurs en système international d'unités si:

1 an = 3.16 x 10⁷ secondes.

1 ua = 150 millions de km = 1.5 x10^onze m.

Et en remplaçant les données de l'équation, nous obtenons une estimation assez réussie du soleil du soleil en 2.0 x 10 ³⁰ kg.

Exercices

Bien que Kepler n'avait que les planètes à l'esprit que lorsqu'il a dérivé ses célèbres lois, celles-ci sont également valables pour le mouvement des satellites et des autres corps du système solaire, comme nous le verrons ensuite.

- Exercice 1

Sachant que l'orbite de Jupiter est 5.19 fois supérieur à celui de la terre, trouvez la période orbitale de Jupiter.

Solution

Selon la définition de l'unité astronomique, Jupiter vient du soleil 5.19 UA, par conséquent, selon la troisième loi de Kepler:

T²= r³= (5.19)³ années

Donc T = (5.19)^3/2  années = 11.8 années

- Exercice 2

Halley Comet visite le soleil tous les 75.3 ans. Trouver:

a) Le semi-cohésion majeure de son orbite.

b) la mesure de l'apélium, si le périhélium mesure 0.568 UA.

Solution

Halley Comet visite le soleil tous les 75.3 ans. Trouver:

a) Le semi-cohésion majeure de son orbite.

b) la mesure de l'apélium, si le périhélium mesure 0.568 UA.

Solution à

Lorsqu'une planète ou toute autre étoile est à son point le plus proche du soleil, il est dit qu'il est dans le périhelio, Et quand c'est plus loin, dans aphelion. Dans le cas particulier d'une orbite circulaire, R dans la troisième loi de Kepler est le rayon de l'orbite.

Peut vous servir: constantes antoine: formules, équations, exemples

Cependant, sur l'orbite elliptique, le corps céleste est plus ou moins loin du soleil, étant le semi-mère «A» la moyenne entre l'aprotesse et le périhélium:

figure 3. Aflio et Pehelio. Source: Wikimedia Commons. Forewman / domaine public de Pearson Scott / public

Par conséquent, nous remplaçons R par A dans la troisième loi de Kepler, qui résulte de Halley dans:

T²= A³→ A = (t)²³ → A = (75.3) ²³ Ua = 17.832 UA

Solution B

A = ½ (périhelio + apelio)

17.832 = ½ (0.568+ aflio) → aflio = 2 x 17.832 - 0.568 UA = 35.10 ua.

Expérience

Analyser le mouvement des planètes nécessite des semaines, des mois et même des années d'observation et d'enregistrement minutieux. Mais en laboratoire, une expérience très simple peut être effectuée pour prouver que la loi des égaux de Kepler est remplie.

Pour cela, un système physique est requis dans lequel la force qui régit le mouvement est centrale, une condition suffisante pour que la loi des zones soit remplie. Un tel système se compose d'une masse liée à une corde longue, avec l'autre extrémité du fil fixe à un support.

La pâte sépare un petit angle de sa position d'équilibre et est imprimée une légère impulsion, de sorte qu'elle exécute un mouvement ovale (presque elliptique) sur le plan horizontal, comme s'il s'agissait d'une planète autour du soleil.

Sur la courbe décrite par le pendule, nous pouvons prouver qu'il balaie des zones égales en temps égal, oui:

-Nous considérons des radios vectorielles allant du centre d'attraction (point d'équilibre initial) à la position de la masse.

-Et nous barmos entre deux moments consécutifs de durée égale, dans deux zones différentes du mouvement.

Plus le fil de pendule est long et plus l'angle qui s'écarte de la verticale est bas.

Ensuite, l'ovale décrit s'approche d'une ellipse, comme celle que les planètes voyagent.

Matériaux

-Fil de filetage

-1 pâte ou boule métallique peinte en blanc qui agit comme un pendule

-Règle

-Convoyeur

-Caméra photo avec disque stroboscopique automatique

-Les soutiens

-Deux sources d'éclairage

-Une feuille de papier ou du carton noir

Il peut vous servir: Big Crunch Theory: Histoire, Principes, données pour et contre

Procédure

L'assemblage de la figure est nécessaire pour prendre des photos de plusieurs flashs du pendule car sa trajectoire suit. Pour ce faire, vous devez mettre la caméra juste au-dessus du pendule et de l'album stroboscopique automatique devant l'objectif.

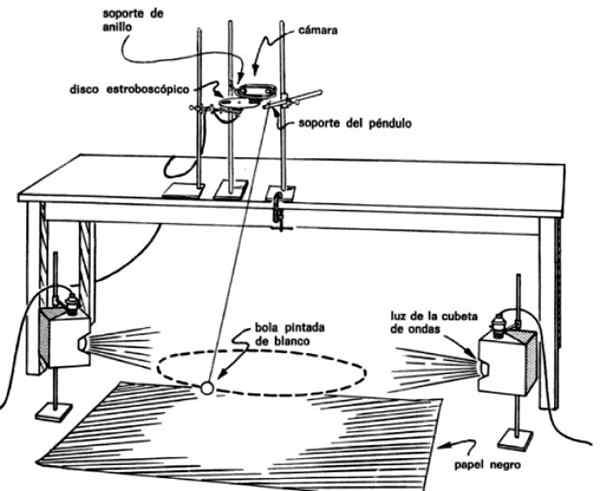Figure 4. Assemblage pendule pour vérifier qu'il balaie des zones égales en temps égal. Source: Guide de laboratoire PSSC.

De cette façon, les images sont obtenues à des intervalles de temps réguliers du pendule, par exemple tous les 0.1 ou tous les 0.2 secondes, ce qui permet de connaître le temps qu'il a fallu pour se déplacer d'un point à l'autre.

Vous devez également éclairer la masse du pendule de manière pratique, en mettant les lumières des deux côtés. La lentille doit être peinte en blanc pour améliorer le contraste en arrière-plan, qui se compose d'un papier noir étendu au sol.

Vous devez maintenant vérifier que le pendule balaie des zones égales dans les temps égaux. Pour cela, un intervalle de temps est choisi et les points occupés par le pendule dans ledit intervalle sont marqués sur papier.

Sur l'image, une ligne est tracée du centre de l'ovale à ces points et nous aurons donc la première des zones balayées par le pendule, qui est approximativement un secteur elliptique comme celui ci-dessous:

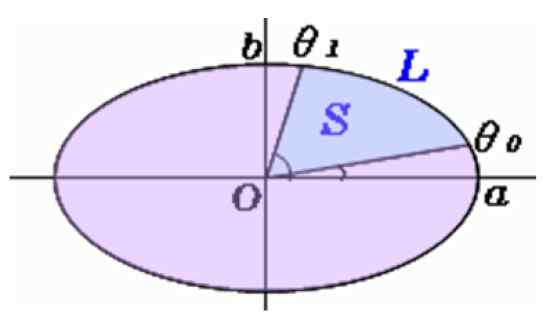Figure 5. Zone d'un secteur elliptique. Source: F. Zapata.

Calcul de la zone de la section elliptique

Les angles sont mesurés avec le convoyeur θ_soit et θ₁, Et cette formule est utilisée pour trouver S, la zone du secteur elliptique:

S = f (θ₁) - f (θ_soit)

Avec F (θ) donné par:

Noter que pour et b Ce sont les semi-Senijes plus grands et mineurs respectivement. Le lecteur ne doit que prendre soin de mesurer soigneusement les semi-morts et les angles, car il existe des calculatrices en ligne pour évaluer facilement cette expression.

Cependant, si vous insistez pour effectuer le calcul à la main, vous devez vous rappeler que l'angle θ est mesuré en degrés, mais au moment de la saisie des données à la calculatrice, les valeurs doivent être exprimées en radianes.

Ensuite, vous devez marquer une autre paire de points dans lesquels le pendule a investi le même intervalle de temps et dessiner la zone correspondante, calculant sa valeur avec la même procédure.

Vérification de la loi des zones égales

Enfin, il reste à vérifier que la loi des zones est remplie, c'est-à-dire que dans les zones égales égales est le balayage.

Les résultats sont-ils un peu dévoués de ce que l'on attend? Vous devez garder à l'esprit que toutes les mesures sont accompagnées de leur erreur expérimentale respective.

Les références

1. Calculatrice en ligne de Keisan. Zone d'une calculatrice du secteur elliptique. Récupéré de: Keisan.Casio.com.
2. OpenTax. Loi de Kepler sur le mouvement planétaire. Récupéré de: OpenStax.org.
3. PSSC. Physique de laboratoire. Éditorial Revered. Récupéré de: livres.Google.co.
4. Palen, s. 2002. Astronomie. Série Schaum. McGraw Hill.
5. Pérez R. Système simple avec force centrale. Récupéré de: Francesphysics.Blogspot.com
6. Stern, D. Les trois lois Kepler du mouvement planétaire. Récupéré de: Phy6.org.