Historique descriptif des statistiques, caractéristiques, exemples, concepts

La statistiques descriptives C'est la branche des statistiques qui traite de la collecte et de l'organisation d'informations sur le comportement des systèmes avec de nombreux éléments, génériquement connu sous le nom de nom de Ville.

Pour cela, il utilise des techniques numériques et graphiques, à travers lesquelles il présente des informations, sans faire de prédictions ou d'inférences sur la population où elle vient.

Les statistiques descriptives sont réputées organiser et présenter les informations de manière pratique

[TOC]

Histoire

Âge antique

Les statistiques ont ses origines dans le besoin humain d'organiser les informations nécessaires à sa survie et à sa puits, ainsi que pour subvenir aux besoins des événements qui l'affectent. Les grandes civilisations de l'antiquité ont laissé des dossiers de colons, des taxes perçues, du montant des cultures et de la taille des armées.

Par exemple, pendant son long règne, Ramsès II (1279-1213 à.C) a ordonné un recensement des terres et des habitants en Égypte, qui avaient alors environ 2 millions d'habitants.

De même, la Bible que Moïse a exécuté un recensement pour savoir combien de soldats avaient les douze tribus d'Israël.

Également dans les anciens, des dénombrements de personnes et de ressources ont été fabriqués. Les Romains, notables pour leur grande organisation, ont enregistré périodiquement la population, préparant les recensements tous les cinq ans, y compris les territoires et les ressources.

Renaissance

Après la baisse de Rome, les documents statistiques importants ont eu peur, jusqu'à l'arrivée de la Renaissance, lorsque les statistiques remontent.

Culminant le XVIIe siècle, la théorie des probabilités est née, le résultat de l'inclinaison des gens pour le jeu, qui a fourni des statistiques la rigueur mathématique qui en a fait une science à part entière.

Âge moderne

Une nouvelle impulsion est venue avec la théorie des erreurs et les carrés minimums au XIXe siècle, qui ont suivi la méthode de corrélation entre les variables, pour évaluer quantitativement la relation entre eux.

Jusqu'à enfin, au cours du XXe siècle, les statistiques s'étendent à chaque branche de la science et de l'ingénierie comme un outil indispensable dans la résolution de problèmes.

Caractéristiques des statistiques descriptives

Les statistiques descriptives sont caractérisées par:

- Organiser les informations collectées dans les données et les graphiques. Les graphiques peuvent être divers: histogrammes, polygones de fréquence, diagrammes en forme de gâteau, entre autres.

- Distribuer des données dans des gammes de fréquences pour faciliter leur gestion. Utilisez l'arithmétique pour trouver les valeurs les plus représentatives des données, par le biais de mesures de tendance centrale, ainsi que pour analyser leur dispersion.

- Déterminez la forme des distributions, leur symétrie, si elles sont centrées ou biaisées, et si elles sont pointues ou plutôt aplaties.

Peut vous servir: dérivés implicites: comment ils sont résolus et résolus des exercices

Que sont les statistiques descriptives pour?

Chaque fois que c'est nécessaire.

Ensuite, nous mentionnons quelques exemples:

Économie

Les statistiques descriptives traitent de l'enregistrement et de l'organisation de données sur les populations et leur âge, leurs revenus, leurs investissements, leurs bénéfices et leurs dépenses. De cette façon, les gouvernements et les institutions planifèrent des améliorations et investissent de manière appropriée.

Avec votre aide, vous surveillez l'efficacité des achats, des ventes, des rendements et des services. Pour cette raison, les statistiques sont indispensables dans la prise de décision.

Physique et mécanique

La physique et la mécanique utilisent des statistiques pour l'étude des milieux continus, qui consistent en un grand nombre de particules, telles que les atomes et les molécules. Il s'avère qu'il n'est pas possible de surveiller chacun d'eux séparément.

Mais en étudiant le comportement global du système (une partie de gaz, par exemple) du point de vue macroscopique, il est possible de découvrir les moyennes et de définir des variables macroscopiques pour connaître ses propriétés. Un exemple de ceci est la théorie cinétique des gaz.

Médecine

C'est un outil essentiel lors de la surveillance des maladies, de ses origines et pendant son évolution, ainsi que l'efficacité des traitements.

Les statistiques qui décrivent les taux de morbidité, de guérison, de temps d'incubation ou de développement d'une maladie, l'âge où il apparaît généralement et les données de style, sont nécessaires lors de la conception des traitements les plus efficaces.

Nutrition

L'une des nombreuses applications des statistiques descriptives est de s'inscrire et de commander des données sur la consommation de nourriture dans les différentes populations: leur quantité, leur qualité et qui sont les plus consommées, entre autres observations qui intéressent les experts.

Exemples de statistiques descriptives

Ci-dessous, nous verrons quelques exemples qui illustrent à quel point les outils des statistiques descriptifs sont utiles pour aider à prendre des décisions:

Exemple 1

Pour améliorer les salles à manger scolaires, les informations sur les utilisateurs sont requises. Source: Wikimedia Commons.

Les autorités éducatives d'un pays plan des améliorations institutionnelles. Supposons qu'ils mettent en œuvre un nouveau système de salles à manger scolaires.

Pour cela, il est nécessaire d'avoir des données sur la population étudiante, par exemple le nombre d'élèves par grade, leur âge, leur sexe, leur taille, leur poids et leur condition socio-économique. Ensuite, ces informations sont présentées sous forme de tables et de graphiques.

Exemple 2

Pour surveiller l'équipe de football locale et faire de nouvelles signatures, les managers portent le nombre de matchs joués, gagnés, liés et perdus, ainsi que le nombre de buts, les buteurs et comment ils ont réussi à marquer: coup franc, à moitié tribunal, pénalités, avec la jambe gauche ou la droite, entre autres détails.

Il peut vous servir: événements mutuellement exclusifs: propriétés et exemples

Exemple 3

Un magasin de crème glacée a plusieurs saveurs de crème glacée et veut améliorer leurs ventes, donc les propriétaires effectuent une étude où ils comptent le nombre de clients, les séparent en groupes par sexe et tranche d'âge.

Dans cette étude, le goût de la crème glacée préférée et la présentation la plus vendue sont enregistrées, par exemple. Et avec les données recueillies, ils prévoient les achats des saveurs et les conteneurs et accessoires nécessaires pour leur préparation.

Concepts de base des statistiques descriptives

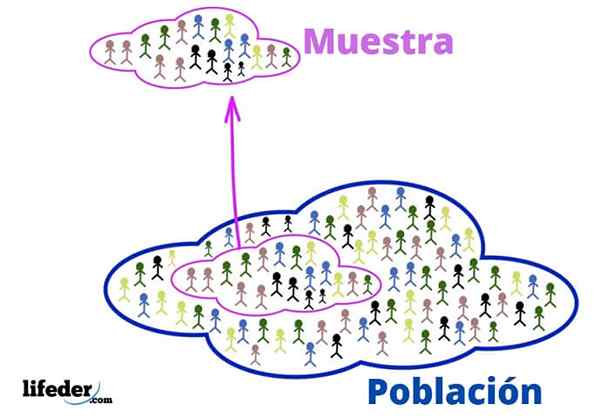Population et échantillon

Ces concepts fondamentaux sont nécessaires pour appliquer des techniques statistiques, voyons: voir:

Ville

Dans le contexte statistique, la population se réfère à l'univers ou au collectif à partir de laquelle les informations proviennent.

Il ne s'agit pas toujours des gens, car ils peuvent être des ensembles d'animaux, de plantes ou d'objets tels que des voitures, des atomes, des molécules et même des événements et des idées.

Goûter

Lorsque la population est très importante, un échantillon représentatif est extrait de celui-ci et analysé, sans perdre des informations pertinentes.

Il peut être choisi au hasard, ou selon certains critères précédemment établis par l'analyste. L'avantage est que le fait d'être un sous-ensemble de la population, il est beaucoup plus gérable.

Variable

Il se réfère à l'ensemble des valeurs qui peuvent prendre une certaine caractéristique de la population. Une étude peut contenir diverses variables, telles que l'âge, le sexe, le poids, le niveau académique, l'état civil, le revenu, la température, la couleur, le temps et bien d'autres.

Les variables peuvent être de nature différente, il existe donc des critères pour les classer et leur donner le traitement le plus approprié.

Variables catégorielles et variables numériques

Selon la façon dont ils sont mesurés, les variables peuvent être:

-Catégorique

-Numérique

Les variables catégorielles, également appelées qualitatif, Ils représentent des qualités telles que le statut civil d'une personne, qui peut être célibataire, mariée, divorcée ou veuve.

D'un autre côté, à des variables numériques ou quantitatif, Ils peuvent être mesurés, comme l'âge, le temps, le poids, les revenus et plus.

Les graphismes sont très importants pour présenter les informations, car en un coup d'œil, la tendance des données est appréciée. Source: piqsels.

Variables variables discrètes et continues

Les variables discrètes ne prennent que des valeurs discrètes, comme son nom implique. Des exemples d'entre eux sont le nombre d'enfants d'une famille, combien de sujets sont dans un certain cours et la quantité de voitures dans un parking.

Ces variables ne prennent pas toujours des valeurs entières, car il y a aussi des fractionnaires.

D'un autre côté, les variables continues admettent des valeurs infinies dans une certaine plage, comme le poids d'une personne, le pH du sang, le temps d'une consultation téléphonique et le diamètre des balles de football.

Peut vous servir: symétrie

Mesures de tendance centrale

Donnez une idée de la tendance générale que les données suivent. Nous mentionnerons les trois mesures centrales les plus utilisées:

-Moitié

-Médian

-Mode

Moitié

Équivalent aux valeurs moyennes. Il est calculé en ajoutant toutes les observations et en divisant entre le nombre total:

 Où x_Toi C'est toute observation et n est le total d'entre eux.

Mode

C'est la valeur qui se répéte le plus dans un ensemble de données, la plus fréquente, car dans une distribution, il peut y avoir plus d'une mode.

Médian

Lors de la commande d'un ensemble de données, la médiane est la valeur centrale de tous.

Mesures de dispersion

Ils soulignent la variabilité des données et donnent une idée de la distance ou de la dispersion des mesures centrales. Les plus utilisés sont:

Gamme

C'est la différence entre la plus grande valeur x_M Et le plus petit x_m d'un ensemble de données:

Plage = x_M - X_m

Variance

Mesurez à quel point les données de valeur moyenne sont. Pour cela, une moyenne est faite, mais avec les différences entre toute valeur x_Toi et la moyenne, au carré pour les empêcher de s'annuler. Il est généralement indiqué par la lettre grecque σ carré, ou avec s²:

Écart-type

La variance n'a pas les mêmes unités que les données, de sorte que l'écart type est défini comme la racine carrée de la variance et est indiqué comme σ ou S:

Fréquence des distributions

Au lieu de prendre en compte chaque données individuellement, il est préférable de les regrouper dans des gammes, ce qui facilite le travail, surtout s'il existe de nombreuses valeurs. Par exemple, lorsque vous travaillez avec les enfants d'une école, ils peuvent être regroupés en tranches d'âge: de 0 à 6 ans, de 6 à 12 ans et de 12 à 18 ans.

Graphiques

Ils constituent un excellent moyen d'apprécier la distribution des données de vue et contiennent toutes les informations recueillies dans les tables et les photos, mais beaucoup plus abordables.

Il y en a une grande variété: avec des barres, linéaire, circulaire, de la tige et des feuilles, des histogrammes, des polygones et pictogrammes de fréquence. Des exemples de graphiques statistiques sont présentés dans la figure 3.

Thèmes d'intérêt

Branches statistiques.

Variables statistiques.

Population et échantillon.

Statistiques déductives.

Les références

1. Faraldo, P. Statistiques et méthodologie de recherche. Récupéré de: eio.USC.est.
2. Fernández, s. 2002. Statistiques descriptives. 2e. Édition. Éditorial ESIC. Récupéré de: Google Books.
3. Historique des statistiques. Récupéré de: Eumed.filet.
4. Ibañez, P. 2010. Mathématiques II. Approche de compétence. Cengage Learning.
5. Monroy, s. 2008. Statistiques descriptives. 1er. Édition. Institut national polytechnique du Mexique.
6. Formules d'univers. Statistiques descriptives. Récupéré de: universoformules.com.