Historique des statistiques inférenties, caractéristiques, à quoi sert, exemples

La Statistiques déductives ou des statistiques déductives sont celles qui déduisent les caractéristiques d'une population d'échantillons en extrait, à travers une série de techniques d'analyse. Avec les informations obtenues, les modèles sont élaborés qui permettent ensuite des prédictions sur le comportement de ladite population.

Par conséquent, les statistiques inférentielles sont devenues la science numéro un pour offrir de la subsistance et des instruments dont les innombrables disciplines ont besoin, lors de la prise de décisions.

La physique, la chimie, la biologie, l'ingénierie et les sciences sociales, bénéficient en continu de ces outils lorsqu'ils créent leurs modèles et leur conception et mettent en œuvre des expériences.

[TOC]

Bref historique des statistiques inférentielles

Les statistiques sont survenues dans les temps anciens en raison de la nécessité de personnes pour organiser les choses et optimiser les ressources. Avant l'invention de l'écriture, des enregistrements du nombre de personnes et de bétail ont été effectués, à travers des symboles enregistrés dans la pierre.

Plus tard, les dirigeants chinois, babyloniens et égyptiens ont laissé des données sur la quantité de cultures et le nombre d'habitants, enregistrés sur des comprimés d'argile, des colonnes et des monuments.

Empire romain

Lorsque Rome a exercé son domaine en Méditerranée, il était courant que les autorités effectuent des recensements tous les cinq ans. En fait, le mot "statistique" vient du mot italien statista, Que signifie exprimer.

En parallèle, en Amérique, les grands empires pré-colombiens ont également apporté des records similaires.

Moyen-Age

Au Moyen Âge, les gouvernements d'Europe, ainsi que l'Église, ont enregistré la propriété de la Terre. Ensuite, ils ont fait de même avec les naissances, les baptêmes, les mariages et les décès.

Âge moderne

La statistique anglaise John Graunt (1620-1674) a été la première à faire des prédictions basées sur de telles listes, telles que le nombre de personnes qui pouvaient mourir de certaines maladies et la proportion estimée de naissances des femmes et des hommes. Par conséquent, le père de la démographie est considéré.

Époque contemporaine

Plus tard, avec l'avènement de la théorie des probabilités, les statistiques ont cessé d'être une simple collection de techniques organisationnelles et ont atteint une portée insoupçonnée en tant que science prédictive.

Ainsi, les experts ont pu.

Caractéristiques

Ci-dessous, nous avons les caractéristiques les plus pertinentes de cette branche des statistiques:

- Des statistiques inférentielles étudient une population qui en tire un échantillon représentatif.

- La sélection des échantillons est effectuée par différentes procédures, la plus appropriée étant celles qui choisissent les composants au hasard. Ainsi, tout élément de la population a la même probabilité d'être choisi et avec lui, les biais indésirables sont évités.

Peut vous servir: comment convertir à partir de km / h a m / s? Exercices résolus

- Pour organiser les informations collectées, il utilise des statistiques descriptives.

- Sur l'échantillon, les variables statistiques sont calculées qui servent à estimer les propriétés de la population.

- Les statistiques inférentielles ou déductives utilisent la théorie des probabilités pour étudier les événements aléatoires, c'est-à-dire ceux qui surgissent. Chaque événement se voit attribuer une certaine probabilité d'occurrence.

- Construisez des hypothèses -UPOSITIONS - sur les paramètres de la population et les contraster, pour savoir s'ils sont corrects et calculent également le niveau de confiance de la réponse, c'est-à-dire qu'il offre une marge d'erreur. La première procédure est appelée tests d'hypothèse, Tandis que la marge d'erreur est le intervalle de confiance.

Que sont les statistiques descriptives pour? Applications

Statistiques inférentielles: essentiel pour prendre des décisions et un contrôle de la qualité

Étudier dans son intégralité une population pourrait exiger de nombreuses ressources en argent, en temps et en efforts. Il est préférable de prélever des échantillons représentatifs qui sont beaucoup plus gérables, de collecter des données à travers eux et de créer des hypothèses ou des hypothèses sur le comportement de l'échantillon.

Une fois les hypothèses établies et leur validité contrastée, les résultats s'étendent à la population et sont utilisés pour prendre des décisions.

Ils aident également à créer des modèles de cette population, pour faire de futures projections. C'est pourquoi les statistiques inférentielles sont une science très utile pour:

Sociologie et études démographiques

Ce sont des champs d'application idéaux, car les techniques statistiques s'appliquent à l'idée d'établir divers modèles de comportement humain. Quelque chose que a priori est assez compliqué, car de nombreuses variables interviennent.

En politique, beaucoup de choses sont utilisées dans le temps des élections pour connaître la tendance des votes électorales, de cette façon les parties de conception des parties.

Ingénierie

Les méthodes de statistiques inférentielles sont largement utilisées dans l'ingénierie, les applications les plus importantes étant le contrôle de la qualité et l'optimisation des processus, par exemple, l'amélioration des temps dans l'exécution des tâches, ainsi que dans la prévention des accidents professionnels.

Économie et administration des affaires 

Avec les méthodes déductives, les projections peuvent être effectuées sur le fonctionnement d'une entreprise, le niveau de ventes attendu, ainsi que de l'aide lors de la prise de décisions.

Par exemple, vos techniques peuvent être utilisées pour estimer la réaction des acheteurs à un nouveau produit, près d'être lancé sur le marché.

Il sert également à évaluer les modifications des habitudes de consommation des personnes, étant donné des événements importants, tels que l'épidémie covide.

Exemples de statistiques inférentielles

Exemple 1

Un simple problème statistique déductif est le suivant: un professeur de mathématiques est en charge de 5 sections d'algèbre élémentaire dans une université et décide d'utiliser les notes moyennes d'un single de leurs sections pour estimer la moyenne de tous.

Peut vous servir: mesure approximative des figures amorphes: exemple et exerciceAussi grande qu'une population puisse être étudiée via un échantillon représentatif. Source: Pixabay.

Une autre possibilité est de prélever un échantillon de chaque section, d'étudier ses caractéristiques et d'étendre les résultats à toutes les sections.

Exemple 2

Le directeur d'un magasin de vêtements pour dames veut savoir combien un certain chemisier sera vendu pendant la saison estivale. Pour ce faire, analysez les ventes de vêtements au cours des deux premières semaines de la saison et déterminez ainsi la tendance.

Concepts de base dans les statistiques inférentielles

Il existe plusieurs concepts clés, y compris ceux qui proviennent de la théorie des probabilités, qui est nécessaire pour avoir clair pour comprendre toute la portée de ces techniques. Certains, en tant que population et échantillon, nous avons déjà mentionné tout au long du texte.

Événement

Un événement ou un événement est quelque chose qui se produit, et qui peut avoir plusieurs résultats. Un exemple d'événement peut être de lancer une devise et il y a deux résultats possibles: le visage ou le sceau.

Espace d'échantillon

C'est l'ensemble de tous les résultats possibles d'un événement.

Population et échantillon

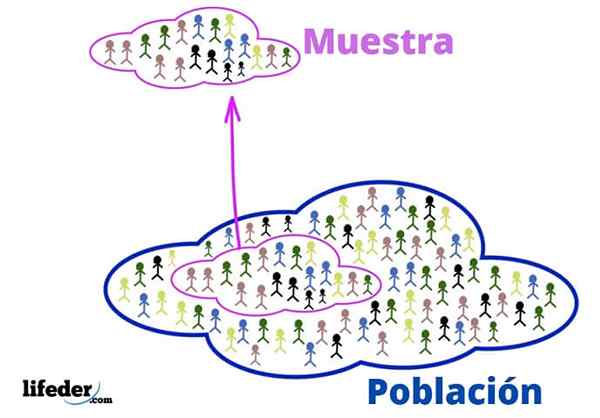Population et échantillon

La population est l'univers à étudier. Ils ne concernent pas nécessairement des personnes vivantes ou des êtres, car la population, en statistiques, peut être composée d'objets ou d'idées.

Pour sa part, l'échantillon est un sous-ensemble de la population, extrait de celui-ci avec soin pour être représentatif.

Échantillonnage

C'est l'ensemble des techniques à travers lesquelles un échantillon est sélectionné dans une population donnée. L'échantillonnage peut être aléatoire si des méthodes probabilistes sont utilisées pour choisir l'échantillon, ou non probabiliste, si l'analyste a un propre critère de sélection, selon leur expérience.

Variables statistiques

Ensemble de valeurs qui peuvent avoir les caractéristiques de la population. Ils sont classés de plusieurs manières, par exemple, ils peuvent être discrets ou continus. De plus, selon leur nature, ils peuvent être qualitatifs ou quantitatifs.

Distributions de probabilité

Fonctions de probabilité décrivant le comportement d'un grand nombre de systèmes et de situations observées dans la nature. Les plus connus sont la distribution gaussienne ou la cloche de Gauss et la distribution binomiale.

Paramètres et statistiques 

La théorie de l'estimation établit qu'il existe une relation entre les valeurs de la population et celles de l'échantillon prélevées de cette population. Les paramètres Ce sont les caractéristiques de la population que nous ne connaissons pas mais nous voulons estimer: par exemple la moyenne et l'écart type.

Pour sa part, le statistique sont les caractéristiques de l'échantillon, par exemple son écart moyen et standard.

Par exemple, supposons que la population se compose de tous les jeunes entre 17 et 30 ans d'une communauté, et il est souhaité connaître la proportion de ceux actuellement dans l'enseignement supérieur. Ce serait le paramètre de population à déterminer.

Peut vous servir: interpolation linéaire

Pour l'estimer, un échantillon aléatoire de 50 jeunes est sélectionné et la proportion d'études dans une université ou un institut d'enseignement supérieur est calculée. Cette proportion est la statistique.

Si l'étude est réalisée, il est déterminé que 63% des 50 jeunes étudient plus haut, c'est la population estimée, fabriquée à partir de l'échantillon.

Ceci est juste un exemple de ce que les statistiques inférentielles peuvent faire. Il est connu sous le nom d'estimation, mais il existe également des techniques pour prédire les variables statistiques, ainsi que pour prendre des décisions.

Hypothèse statistique

C'est une conjecture qui est faite concernant la valeur de la moyenne et l'écart type de certaines caractéristiques de la population. À moins que la population ne soit complètement examinée, ce sont des valeurs inconnues.

Tests d'hypothèse

Les hypothèses sont-elles faites sur les paramètres de population valides? Pour le savoir, il est vérifié si les résultats de l'échantillon les soutiennent ou non, il est donc nécessaire de concevoir des tests d'hypothèse.

Ce sont les étapes générales pour en effectuer une:

Étape 1

Identifier le type de distribution que la population devrait suivre.

Étape 2

Soulever deux hypothèses, indiquées h_soit et h₁. Le premier est le hypothèse nulle dans lequel nous supposons que le paramètre a une certaine valeur. Le second est L'hypothèse alternative qui est une valeur différente de l'hypothèse nulle. Si cela est rejeté, l'hypothèse alternative est acceptée.

Étape 3

Établir une marge acceptable pour la différence entre le paramètre et la statistique. Ils seront rarement identiques, bien qu'ils soient censés être très proches.

Étape 4

Proposer un critère pour accepter ou rejeter l'hypothèse nulle. Pour cela, une statistique de test est utilisée qui peut être la moyenne. Si la valeur moyenne est dans certaines limites, l'hypothèse nulle est acceptée, sinon elle est rejetée.

Étape 5

En dernière étape, il est décidé si l'hypothèse nulle est acceptée ou non.

Thèmes d'intérêt

Branches statistiques.

Variables statistiques.

Population et échantillon.

Statistiques descriptives.

Les références

1. Berenson, M. 1985.Statistiques pour l'administration et l'économie, les concepts et les applications. Éditorial inter-américain.
2. Canavos, g. 1988. Probabilité et statistiques: applications et méthodes. McGraw Hill.
3. Devore, J. 2012. Probabilité et statistiques pour l'ingénierie et la science. 8e. Édition. Cengage Learning.
4. Historique des statistiques. Récupéré de: Eumed.filet.
5. Ibañez, P. 2010. Mathématiques II. Approche de compétence. Cengage Learning.
6. Levin, R. 1981. Statistiques pour les administrateurs. Prentice Hall.
7. Walpole, R. 2007. Probabilité et statistiques pour l'ingénierie et la science. Pearson.