Formule d'erreur aléatoire et équations, calcul, exemples, exercices

Il erreur aléatoire d'une quantité physique se compose des variations non prévisibles de la mesure de ce montant. Ces variations peuvent être produites par le phénomène qui est mesuré, par l'instrument de mesure ou par l'observateur lui-même.

Une telle erreur n'est pas due au fait que quelque chose a été mal fait pendant l'expérience, mais qu'il s'agit d'une erreur inhérente au processus de mesure ou au phénomène étudié. Cela provoque la mesure mesurée parfois un peu plus grande et parfois un peu inférieure, mais oscille généralement autour d'une valeur centrale.

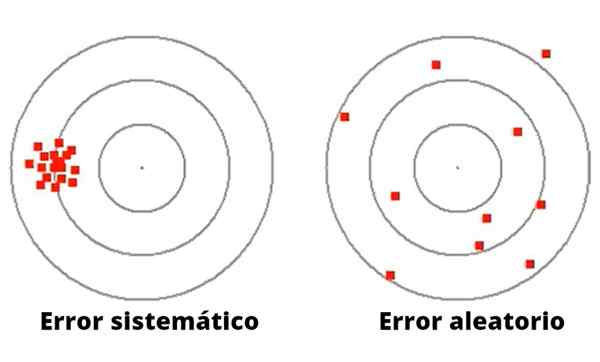
Figure 1- Les erreurs aléatoires varient en amplitude et en direction. Au contraire, les erreurs systématiques ont tendance à être cohérentes.

Contrairement à une erreur aléatoire, une erreur systématique peut être causée par un mauvais étalonnage ou un facteur d'échelle inapproprié dans l'instrument de mesure, y compris une défaillance dans l'équipement expérimental, ou une observation inappropriée, ce qui provoque une déviation dans le même sens.

La figure 1 illustre la différence entre l'erreur systématique et aléatoire dans le jeu de lancement de Dart vers une cible avec cercles.

Dans le cas de la gauche, les fléchettes sont concentrées autour d'un très loin du centre. Le lanceur de ces fléchettes, bien que de bon objectif, a une défaillance systématique, peut-être d'origine visuelle, ou de lancer.

D'un autre côté, le lanceur à droite (dans la figure 1) a une grande dispersion autour de la cible centrale, c'est donc un pichet très imprécis, avec un mauvais objectif, qui fait involontairement une erreur aléatoire.

[TOC]

Formules et équations en erreur aléatoire

Lorsque le processus de mesure montre une erreur aléatoire, c'est nécessaire.

Bien sûr, dans chaque mesure, il est nécessaire de prendre soin que les conditions dans lesquelles elles sont effectuées sont toujours les mêmes.

Peut vous servir: Faraday Law: formule, unités, expériences, exercice,

Supposons que la mesure soit répétée n fois. Comme il y a une erreur aléatoire dans chaque mesure, il y aura une valeur légèrement différente. Supposons que l'ensemble de n Les mesures sont:

X₁, X₂, X₃,…, X_n

Alors quel rapport de valeur pour la mesure? 

Valeur moyenne et écart-type

Le valeur moyenne soit moyenne de l'ensemble des mesures, que nous désignons et est calculé comme suit:

= (x₁ + X₂ + X₃ +… + X_n) / n

Écart-type

Cependant, ce résultat a une marge d'erreur donnée par l'écart type. Pour le définir, vous devez d'abord connaître la déviation puis la variance:

-La déviation d_Toi  que chaque valeur mesurée a Xi En ce qui concerne la valeur moyenne est:

d_Toi = x_Toi -

Si la moyenne des écarts était calculée, elle serait systématiquement obtenue = 0, car: 

= (D₁ + d₂ + d₃ +… + D_n) / n =

= [x₁ - ) + (x₂ - ) +… + (X_n - )] / n

= (x₁+ X₂ +… + X_n) / n - n / n = - = 0

-La moyenne des écarts n'est pas utile pour connaître la dispersion des mesures. En revanche, la valeur moyenne du carré d'écarts ou de variance, indiquée par σ², Oui il l'est.

Il est calculé selon la formule suivante:

σ² = (D₁² + d₂² +.. .+ d_n² ) / (N -1)

En statistiques, ce montant est appelé variance.  

Et à la racine carrée de la variance, il est connu sous le nom Écart type σ:

σ = √ [(d₁² + d₂² +.. .+ d_n² ) / (n -1)] 

L'écart type σ indique que:

1.- 68% des mesures effectuées sont incluses dans l'intervalle [- σ, + σ]. 

2.- 95% des mesures sont dans l'intervalle [- 2σ, + 2σ].

3.- 99,7% des mesures prises se trouvent dans la plage [- 3σ, + 3σ].

Comment calculer l'erreur aléatoire?

Le résultat de la mesure est le valeur moyenne des n Mesures indiquées et calculées selon la formule suivante:

Peut vous servir: Areolar Speed: Comment il est calculé et les exercices résolus

= (∑x_Toi) / n

Cependant, ce n'est pas la valeur "exacte" de la mesure, car elle est affectée par le Erreur aléatoire ε, qui est calculé comme ceci:

ε = σ / √n

Où:

σ = √ [(∑ (xi -)² ) / (n -1)]

Le résultat final de la mesure doit être signalé de toutes les manières suivantes:

1. ± σ / √n = ± ε Avec un niveau de confiance de 68%.
2. ± 2σ / √n = ± 2ε Avec un niveau de confiance à 95%.
3. ± 3σ / √n = ± 3ε Avec un niveau de confiance de 99,7%.

L'erreur aléatoire affecte la dernière figure significative de la mesure, qui coïncide généralement avec l'appréciation de l'instrument de mesure. Cependant, si l'erreur aléatoire est très grande, les deux derniers chiffres significatifs peuvent être affectés par la variation.

Exemples d'erreur aléatoire

Des erreurs aléatoires peuvent apparaître dans divers cas dans lesquels une mesure est faite:

Mesurer une longueur avec un ruban à mesurer ou une règle

Lorsqu'une longueur est mesurée avec une règle ou un ruban à mesurer et que les lectures se situent entre les marques de l'échelle, alors cette valeur intermédiaire est estimée.

Parfois, l'estimation a un excès et d'autres défauts, donc une erreur aléatoire est introduite dans le processus de mesure.

Figure 2. Les erreurs aléatoires peuvent apparaître lorsqu'une longueur est mesurée avec un ruban adhésif. Source: pikrepo.

La vitesse du vent

Dans la mesure de la vitesse du vent, il peut y avoir des changements dans la lecture d'un moment à un autre, en raison de la nature changeante du phénomène.

Lors de la lecture du volume dans un cylindre gradué

Lorsque le volume est lu avec un cylindre gradué, même en essayant de minimiser l'erreur de parallage, chaque fois qu'elle est mesurée, l'angle d'observation méniscale change un peu, c'est pourquoi les mesures sont affectées par une erreur aléatoire.

Il peut vous servir: Première condition d'équilibre: explication, exemples, exercices figure 3.- Dans le laboratoire de chimie, il est possible de commettre des erreurs aléatoires dans la lecture d'un cylindre de diplômé. Source: Pexels.

Lorsque la stature d'un enfant est mesurée

En mesurant la hauteur d'un enfant, surtout s'il est un peu agité, il fait que de petites modifications de posture changent légèrement la lecture.

Lorsque vous utilisez l'échelle de la salle de bain

Lorsque nous voulons mesurer notre poids avec une salle de bain, un petit changement dans le point de support, même un changement de position peut affecter au hasard la mesure.

Exercice résolu

Une poussette de jouet est autorisée à rouler le long d'une piste droite et inclinée et mesurée avec un chronomètre du temps qui prend toute la piste. 

La mesure est effectuée 11 fois, avec la prise en charge de libérer le chariot du même endroit, sans donner d'impulsion et garder les correctifs d'inclinaison.

L'ensemble des résultats obtenus est:

3,12S 3.09S 3.04S 3.04S 3.10S 3.08S 3.05S 3.10S 3.11S 3.06S, 3.03S

Quelle est l'erreur aléatoire des mesures?

Figure 4. Prendre le temps d'une strolle de jouets qui descend à travers un avion incliné. Source: Fanny Zapata.

Solution

Comme on peut le voir, les résultats obtenus ne sont pas uniques et varient légèrement.

La première consiste à calculer la valeur de temps de descente moyenne, obtenant 3,074545455 secondes.

Cela n'a aucun sens de maintenir autant de décimales, car chaque mesure a trois chiffres significatifs et la deuxième décimale de chaque mesure est incertaine, car elle est à la limite d'appréciation du chronomètre, donc le résultat est arrondi à deux décimales:

= 3,08 s.

Avec la calculatrice en mode statistique, l'écart type est σ = 0,03 s Et l'erreur standard est σ / √11 = 0,01 s. Le résultat final est exprimé comme suit:

Temps de descente 

3,08 s ± 0,01 s (avec un niveau de confiance de 68%)

3,08 s ± 0,02 s (avec un niveau de confiance à 95%)

3,08 s ± 0,03 s (avec un niveau de confiance de 99,7%)

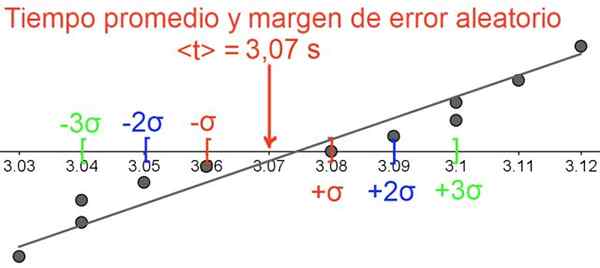Figure 5. La marge d'erreur aléatoire, notez que les données sont regroupées autour de la valeur moyenne. Source: F. Zapata.

Les références

1. Canavos, g. 1988. Probabilité et statistiques: applications et méthodes. McGraw Hill.
2. Devore, J. 2012. Probabilité et statistiques pour l'ingénierie et la science. 8e. Édition. Cengage.
3. Helmestine a. Erreur aléatoire vs. Erreur systématique. Récupéré de: Thoughtco.com
4. Laredo, e. Erreurs moyennes. Récupéré de: USB.aller.
5. Levin, R. 1988. Statistiques pour les administrateurs. 2e. Édition. Prentice Hall.