Fonctions trigonométriques inverses, dérivées, exemples, exercices

Le Fonctions trigonométriques inverses, Comme son nom l'indique, ce sont les fonctions inverses correspondantes des fonctions des sinus, de la tangente, de la cotangente, du séchage et de la moissonneuse.

Les fonctions trigonométriques inverses sont désignées par le même nom de sa fonction trigonométrique directe correspondante plus le préfixe ARC. De cette façon:

1.- Arcsen (x) C'est la fonction trigonométrique inverse de la fonction péché (x)

2.- Arccos (x) C'est la fonction trigonométrique inverse de la fonction cos (x)

3.- Arctan (x) C'est la fonction trigonométrique inverse de la fonction Tan (x)

4.- Arccot ​​(x) C'est la fonction trigonométrique inverse de la fonction COT (X)

5.- ArcSec (x) C'est la fonction trigonométrique inverse de la fonction sec (x)

6.- Arccsc (x) C'est la fonction trigonométrique inverse de la fonction CSC (x)

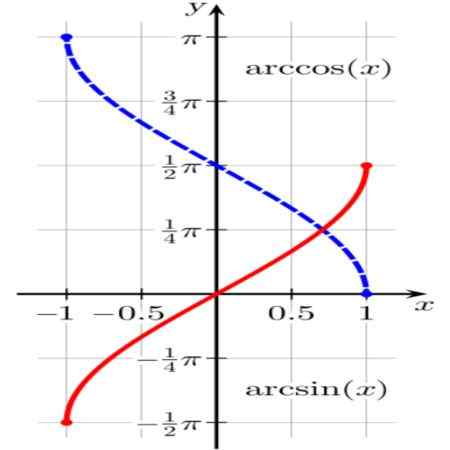
Figure 1. Fonctions arcsen (x) (en rouge) et arccos (x) (en bleu). Source: Wikimedia Commons.

La fonction θ = arcsen (x) Il en résulte un arc unitaire θ (ou angle dans les rayons θ) tel que sin (θ) = x.

Ainsi, par exemple, Arcsen (√3 / 2) = π / 3 Puisqu'il est connu, le sein de π / 3 radians est égal à √3 / 2.

[TOC]

Valeur principale des fonctions trigonométriques inverses

De sorte qu'une fonction mathématique f (x) ait inverse g (x) = f^-1(x) Il est nécessaire que cette fonction soit Injectif, Ce qui signifie que chaque valeur et l'ensemble d'arrivée de la fonction f (x) proviennent d'une et unique valeur x.

Il est clair que cette exigence n'est remplie par aucune fonction trigonométrique. Pour clarifier le point, remarquons que la valeur y = 0,5 peut être obtenue à partir de la fonction sinusale de la manière suivante:

• sin (π / 6) = 0,5
• sin (5π / 6) = 0,5
• sin (7π / 6) = 0,5

Et bien d'autres, puisque la fonction des sinus est périodique avec la période 2π.

Il peut vous servir: Multiples of 8: Que sont et explications

Afin de définir les fonctions trigonométriques inverses, il est nécessaire de restreindre le domaine de leurs fonctions trigonométriques directes correspondantes, afin qu'elles répondent à l'exigence d'injectivité.

Ce domaine restreint de la fonction directe sera la plage ou la branche principale de sa fonction inverse correspondante.

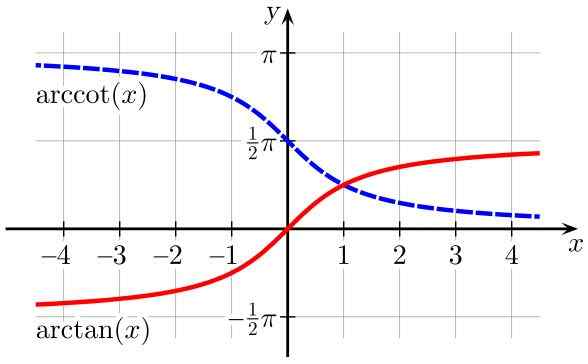Figure 2. Fonctions Arctan (x) (en rouge) et arccot ​​(x) (en bleu). Source: Wikimedia Commons.

Tableau des domaines et gammes des fonctions trigonométriques inverses

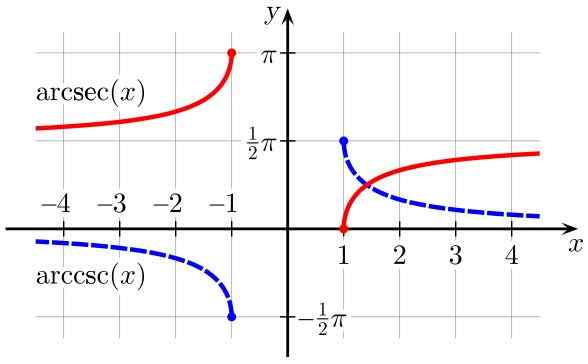figure 3. ArcSec (x) (en rouge) et arccSc (x) (en bleu) (en bleu). Source: Wikimedia Commons.

Dérivé des fonctions trigonométriques inverses

Pour obtenir les dérivés des fonctions trigonométriques inverses, les propriétés des dérivés sont appliquées, en particulier celle dérivée d'une fonction inverse.

Si nous désignons f (y) à la fonction et par f^-1(x) À sa fonction inverse, alors la dérivée de la fonction inverse est liée à la dérivée de la fonction directe à travers la relation suivante:

[F^-1(x)]] '= 1 / f' [f^-1(X)]

Par exemple: si x = f (y) = √y est la fonction directe, son inverse sera

y = f^-1(x) = x². Appliquons la règle de la dérivée inverse à ce cas simple pour voir que cette règle est respectée:

[X²] '= 1 / [√y]' = 1 / (½ et^-½ = 2 et^½ = 2 (x²)^½ = 2x 

Eh bien, nous pouvons évaluer cette astuce pour trouver celles dérivées de fonctions trigonométriques inverses.

Par exemple, nous prenons θ = arcsen (x) En tant que fonction directe, alors sa fonction inverse sera sin (θ) = x.

[arcsen (x)] '= 1 / [sin (θ)]' = 1 / cos (θ) = 1 / √ (1 - sen (θ)²) =…

… = 1 / √ (1 - x²) .

De cette façon, tous ceux dérivés des fonctions trigonométriques inverses peuvent être obtenues, qui sont illustrées ci-dessous:

Figure 4. Tableau de ceux dérivés de fonctions trigonométriques inverses. Source: Wikimedia Commons.

Ces dérivés sont valables pour tout argument z appartenant à des nombres complexes et sont donc également valables pour tout argument réel x, puisque z = x + 0i.

Peut vous servir: quadrilatère: éléments, propriétés, classification, exemples

Exemples

- Exemple 1

Trouver Arctan (1).

Solution

L'ARCTAN (1) est l'arc unitaire (angle dans les rayons) ፀ tel que le tan (ፀ) = 1. Cet angle est ፀ = π / 4 parce que SO (π / 4) = 1. Alors Arctan (1) = π / 4.

- Exemple 2

Calculer Arcsen (cos (π / 3)).

Solution

L'angle π / 3 radians est un angle notable dont le cosinus est ½, de sorte que le problème est réduit à la recherche d'arcsen (½).

Il s'agit donc de trouver l'angle dont le sinus donne ½. Cet angle est π / 6, puisque Sen (π / 6) = sen (30º) = ½. Donc arcsen (cos (π / 3)) = π / 6. 

Exercices

- Exercice 1

Trouvez le résultat de l'expression suivante:

Sec (Arcan (3)) + CSC (ARCCOT (4))

Solution

Nous commençons à nommer α = arcan (3) et β = arcot (4). Donc, l'expression que nous devons calculer est comme ceci:

Sec (α) + CSC (β)

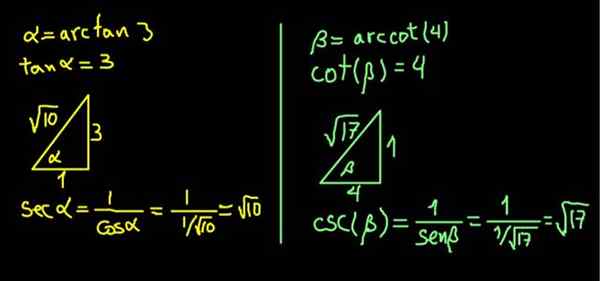
L'expression α = arcan (3) équivaut à le dire (α) = 3.

Comme la tangente est la jambe opposée sur l'adjacent, un triangle rectangle de cateto opposé à α de 3 unités et une catégorie adjacente de 1 unité est construite, de sorte que (α) = 3/1 = 3.

Dans un triangle rectangulaire, l'hypoténuse est déterminée par le théorème de Pythagore. Avec ces valeurs, c'est √10, de sorte que:

sec (α) = hypoténuse / cateto adjacent = √10 / 1 = √10.

De même, β = arcot (4) équivaut à indiquer que Cot (β) = 4.

Un triangle rectangle de cateto adjacent à β de 4 unités et un cateto opposé de 1 unité est construit, de sorte que le COT (β) = 4/1.

Le triangle est immédiatement terminé pour trouver son hypoténuse grâce au théorème de Pythagore. Dans ce cas, il s'est avéré avoir √17 unités. Alors le CSC (β) = hypoténuse / Cateto opposé = √17 / 1 = √17 est calculé.

Il peut vous servir: y = 3sen (4x) période de fonction

Se souvenir que l'expression que nous devons calculer est: 

sec (arcan (3)) + csc (arcot (4)) = sec (α) + csc (β) =…

… = √10 + √17 = 3,16 + 4.12 = 7,28.

- Exercice 2

Trouvez les solutions de:

Cos (2x) = 1 - sen (x)

Solution

Il est nécessaire que toutes les fonctions trigonométriques soient exprimées dans le même argument ou angle. Nous utiliserons l'identité du double angle:

Cos (2x) = 1 - 2 sen²(X)

Ensuite, l'expression originale est réduite à:

1 - 2 sen²(x) = 1 - sin x

Une fois simplifié et factorisé, il est exprimé comme:

sin (x) (2 sen (x) - 1) = 0

Qui donne naissance à deux équations possibles: sin (x) = 0 avec la solution x = 0 et une autre équation Sen (x) = ½ avec x = π / 6 comme solution.

Les solutions à l'équation soulevée sont: x = 0 ou x = π / 6.

- Exercice 3

Trouvez les solutions de l'équation trigonométrique suivante:

cos (x) = sin²(X)

Solution

Pour résoudre cette équation, il est pratique de placer un seul type de fonction trigonométrique, nous utiliserons donc l'identité trigonométrique fondamentale afin que l'équation d'origine soit réécrite comme suit:

cos (x) = 1 - cos²(X)

Si nous nommons y = cos (x), l'expression peut être réécrite comme:

et² + et - 1 = 0

Il s'agit d'une équation au deuxième degré et, dont les solutions sont:

y = (-1 ± √5) / 2

Ensuite, les valeurs de x qui remplissent l'équation d'origine sont:

x = arcos ((-1 ± √5) / 2)

La solution réelle étant le signe positif x = 0,9046 rad = 51,83º.

L'autre solution est complexe: x = (π - 1.06 i) rad.

Les références

1. Hazewinkel, m. 1994. Encyclopédie des mathématiques. Kluwer Publishers académiques / Springer Science & Business Media. 
2. Compagnon mobile. Fonctions trigonométriques inverses. Récupéré de: Matemovil.com
3. Formules d'univers. Fonctions trigonométriques inverses. Récupéré de: universoformules.com
4. Weisstein, Eric W. Inventer les fonctions trigonométriques. Récupéré de: Mathworld.Wolfram.com
5. Wikipédia. Inventer les fonctions trigonométriques. Récupéré de: dans.Wikipédia.com