Détermination de l'équilibre translationnel, applications, exemples

Il Équilibre translationnel C'est un état dans lequel un objet dans son ensemble est lorsque toutes les forces agissant dessus sont compensées, ce qui entraîne une force vide. Mathématiquement, cela équivaut à dire que f₁+ F₂ +  F₃ +.. . = 0, étant f₁, F₂,  F₃... les forces impliquées.

Le fait qu'un corps soit en équilibre translationnel ne signifie pas qu'il est nécessairement au repos. Ceci est un cas particulier de la définition précédente. L'objet peut être en mouvement, mais en l'absence d'accélération, ce sera un mouvement rectiligne uniforme.

Figure 1. L'équilibre de la traduction est important pour un grand nombre de sports. Source: Pixabay.

Donc, si le corps est au repos se poursuit. Et si vous avez déjà du mouvement, il aura une vitesse constante. En général, le mouvement de tout objet est une composition de traductions et de rotations. Les traductions peuvent être comme indiqué dans la figure 2: linéaire ou curviligne.

Mais si l'un des points de l'objet est fixé, alors la seule possibilité de déménagement est de tourner. L'exemple de ceci est un CD, dont le centre est fixé. Le CD a la possibilité de tourner autour d'un axe qui passe par ce point, mais pas de bouger.

Lorsque les objets ont des points fixes ou sont pris en charge sur les surfaces, il est question de des liens. Les liens interagissent limitant les mouvements que l'objet est capable de faire.

[TOC]

Détermination de l'équilibre translationnel

Pour une particule en équilibre, il est valable pour garantir que:

F_R = 0

Ou en notation sommaire:

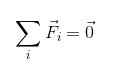
Il est clair que pour qu'un corps soit en équilibre translationnel, les forces qui y agissent doivent être compensées d'une manière ou d'une autre, de sorte que son résultat est vide.

De cette façon, l'objet ne connaîtra pas l'accélération et toutes ses particules sont au repos ou expérimentent des traductions rectilignes à vitesse constante.

Il peut vous servir: Théorie du Big Bang: caractéristiques, étapes, preuves, problèmes

Maintenant, si les objets peuvent tourner, ils le feront généralement. C'est pourquoi la plupart des mouvements sont constitués de combinaisons de traduction et de rotation.

Rotation d'un objet

Lorsque l'équilibre rotationnel est important, il peut être nécessaire de s'assurer que l'objet ne tourne pas. Ensuite, vous devez étudier s'il y a des couples ou des moments qui agissent dessus.

Le couple est l'ampleur du vecteur sur lequel les rotations dépendent. Nécessite qu'une force soit appliquée, mais le point d'application de ceci est également important. Pour clarifier l'idée, considérez un objet étendu sur lequel une force agit F Et voyons si vous êtes en mesure de produire une rotation par rapport à certains axes ou.

Il est déjà intuié qu'en poussant l'objet au point P avec la force F, Il est possible de retourner le point O, avec une direction anti-horaire. Mais la direction dans laquelle la force est appliquée est également importante. Par exemple, la force appliquée sur la figure du milieu ne pourra pas tourner l'objet, bien qu'il puisse certainement le déplacer.

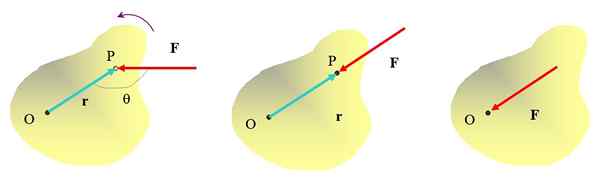Figure 2. Diverses façons d'appliquer une force sur un objet étendu, seulement sur la figure de l'extrême gauche, un effet de rotation est obtenu. Source: auto-faite.

Appliquer la force directement au point ou ne sera pas utilisée pour tourner l'objet non plus. Alors il est clair que pour obtenir un effet de rotation, la force doit être appliquée à une certaine distance de l'axe de rotation et sa ligne d'action ne doit pas passer par cet axe.

Définition du couple

Le couple ou le moment d'une force, désigné comme τ l'amplitude vectorielle responsable de la réduction de tous ces faits, est définie comme:

τ = r X F

Le vecteur r Il est dirigé de l'axe de rotation au point d'application de la force et la participation de l'angle entre R et F est importante. Par conséquent, l'ampleur du couple est exprimée comme suit:

Peut vous servir: Première loi de Newton: formules, expériences et exercices

τ = r.F.Sen q

Le couple le plus efficace a lieu lorsque r et F Ils sont perpendiculaires.

Maintenant, s'il est souhaité qu'il n'y ait pas de rotations ou que celles-ci passent avec une accélération angulaire constante, il est nécessaire que la somme des couples agissant sur l'objet soit nul, analogue à ce qui a été considéré pour les forces:

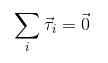
Conditions d'équilibre

L'équilibre signifie stabilité, harmonie et équilibre. Pour que le mouvement d'un objet possède ces caractéristiques, les conditions décrites dans les sections précédentes doivent être appliquées:

1) F₁+ F₂ +  F₃ +.. . = 0

2) τ₁+ τ₂ +  τ₃ +.. . = 0

La première condition garantit l'équilibre translationnel et le second le rotation. Les deux doivent être remplis si l'objet est voulu rester équilibre statique (Absence de mouvement de toute sorte).

Applications

Les conditions d'équilibre sont applicables à de nombreuses structures, car lorsque des bâtiments ou des objets divers sont construits, il est fait avec l'intention que leurs pièces soient maintenues dans les mêmes positions relatives les unes avec les autres. En d'autres termes, que l'objet n'est pas désarmé.

Ceci est important par exemple lors de la construction de ponts qui restent ferme sous leurs pieds, ou lors de la conception de structures habitables qui ne changent pas de position ou ont tendance à vider.

Bien que l'on pense que le mouvement rectiligne uniforme est une simplification extrême du mouvement, qui se produit généralement peu de nature, il faut se rappeler que la vitesse de la lumière dans le vide est constante, et celle du son dans l'air aussi, si considère homogène dans l'environnement.

Dans de nombreuses structures mobiles fabriquées par l'homme, il est important qu'une vitesse constante soit maintenue: par exemple, sur les escaliers mécaniques et les lignes de montage.

Il peut vous servir: deuxième loi de la thermodynamique: formules, équations, exemples

Exemples d'équilibre de translation

C'est l'exercice classique des tensions qui maintiennent la lampe en équilibre. On sait que la lampe pèse 15 kg. Trouvez les amplitudes des tensions nécessaires pour le garder dans cette position.

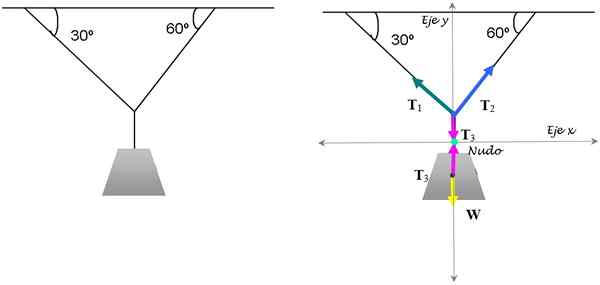figure 3. Le solde de la lampe est garanti en appliquant la condition de bilan de translation. Source: auto-faite.

Solution

Pour le résoudre, nous nous concentrons sur le nœud où les trois cordes se réunissent. Les diagrammes de corps libres respectifs pour le nœud et pour la lampe sont illustrés dans la figure ci-dessus.

Le poids de la lampe est W = 5 kg . 9.8 m / s² = 49 N. Pour que la lampe soit en équilibre, il suffit que la première condition de bilan soit remplie:

T₃ - W = 0

T₃ = W = 49 n.

Des tensions T₁ et T₂ Ils doivent se décomposer:

T_1Y + T_{2 et} - T₃ = 0 (Été des forces le long de l'axe y)))

-T_{1 fois} +T_2x = 0 (Été des forces le long de l'axe x)

Application de la trigonométrie:

T₁.Cos 60º + T₂ .Cos 30º = 49

- T₁.Sen60º + T₂.Sen30º = 0

Il s'agit d'un système de deux équations avec deux inconnues, dont la réponse est: T₁ = 24.5 N et T₂ = 42.4 N.

Les références

1. Rex, un. 2011. Fondamentaux de la physique. Pearson. 76 - 90.
2. SERAY, R., Jewett, J. (2008). Physique pour la science et l'ingénierie. Volume 1. 7^mame. Élégant. Cengage Learning. 120 - 124.
3. SERAY, R., Vulle, c. 2011. Fondamentaux de la physique. 9^{n / A} Élégant. Cengage Learning. 99-112.
4. Tippens, P. 2011. Physique: concepts et applications. 7e édition. Colline de MacGraw. 71 - 87.
5. Walker, J. 2010. La physique. Addison Wesley. 332 -346.