Centre de propriétés de gravité, calcul, exemples

Il centre de gravité d'un corps de taille mesurable est le point où son poids est considéré comme appliqué. C'est donc l'un des principaux concepts de statique.

La première approche des problèmes de physique élémentaire consiste à supposer que tout objet se comporte comme une masse spécifique, c'est-à-dire qu'elle manque de dimensions et que la masse entière est concentrée en un seul point. Ceci est valable pour une boîte, une voiture, une planète ou une particule subatomique. Ce modèle est connu sous le nom modèle de particules.

Figure 1. En hauteur, saut, l'athlète les répare afin que son centre de gravité soit à l'extérieur du corps. Source: Pixabay

Naturellement, c'est une approche, ce qui donne de très bons résultats pour de nombreuses applications. Ce n'est pas une tâche facile de considérer le comportement individuel des milliers et des millions de particules que tout objet pourrait contenir.

Cependant, les vraies dimensions des choses doivent être prises en compte si vous le souhaitez. Puisque nous sommes généralement à proximité immédiate de la Terre, la force toujours présente sur n'importe quel corps est précisément le poids.

[TOC]

Considérations pour trouver le centre de gravité 

Si la taille du corps va être prise en compte, où le poids sera appliqué spécifiquement? Lorsque vous avez un objet continu arbitrairement, son poids est un Force distribuée entre chacune de ses particules constituantes.

Laissez ces particules m₁, m₂, m₃… Chacun d'eux éprouve sa force gravitationnelle correspondante m₁g, m₂g, m₃G ..., tout parallèle. Il en est ainsi, car le champ gravitationnel de la terre est considéré comme constant dans la grande majorité des cas, compte tenu du fait que les objets sont petits par rapport à la taille de la planète et sont proches de sa surface.

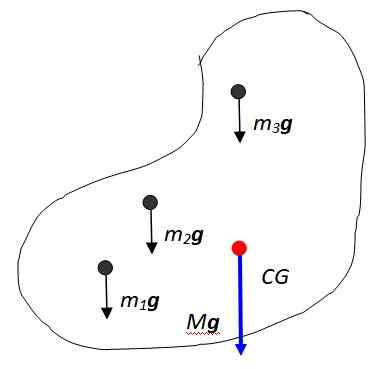Figure 2. Le poids de l'objet est une masse distribuée. Source: auto-faite.

La somme vectorielle de ces forces entraîne le poids de l'objet, appliqué au point appelé le centre de gravité indiqué sur la figure comme CG, qui coïncide ensuite avec le Centre de masse. Le centre de masse à son tour est le point où la masse entière pourrait être considérée comme concentrée.

Le poids résultant a une magnitude Mg où M C'est la masse totale de l'objet, et bien sûr, il est dirigé verticalement vers le centre de la terre. La notation du sumory est utile pour exprimer le corps total du corps:

Les objets symétriques et homogènes, ce qui équivaut à leur densité uniforme, ont leur centre de gravité dans le centre géométrique: cubes, parallèles, anneaux, pneus ou sphères.

Le centre de gravité ne correspond pas toujours à un point de matériau. Par exemple, le CG d'un cerceau est dans son centre géométrique, où il n'y a pas de pâte elle-même. Même ainsi, si vous souhaitez analyser les forces qui agissent sur un cerceau, le poids doit être appliqué à ce point précis.

Dans lequel les cas dans lesquels l'objet est arbitraire, s'il est homogène, son centre de masse peut toujours être calculé en trouvant le centroïde o Baricentro de la figure.

Peut vous servir: Mercure (planète)

Comment le centre de gravité est-il calculé?

En principe, si le centre de gravité (CG) et le centre de masse (CM) coïncident lorsque le champ gravitationnel est uniforme, alors le CM peut être calculé et sur elle appliquer le poids.

Considérez deux cas: le premier est celui dans lequel la distribution de masse est discrète; Autrement dit, vous pouvez compter chaque masse qui forme le système et attribuer un numéro I, comme cela a été fait dans l'exemple précédent.

Les coordonnées du centre de masse pour une distribution de masse discrète sont: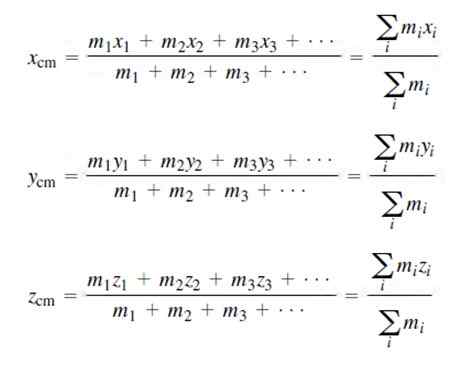

Naturellement, la somme de toutes les masses équivaut à la masse totale du système M, comme indiqué ci-dessus.

Les trois équations sont réduites à une forme compacte lorsque vous envisagez le vecteur r_cm o Vector de position du centre de masse:

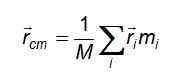
Et en cas de distribution de masse continue, où les particules sont de taille différentielle et ne peuvent pas être distinguées pour les compter, la somme est remplacée par une intégrale qui est faite sur le volume occupé par l'objet en question:

Où r C'est le vecteur de position d'une masse différentielle DM Et la définition de la densité de masse pour exprimer le différentiel de masse a été faite DM contenu dans un différentiel de volume Dv:

La densité de l'objet peut être constante, auquel cas il sort de l'intégrale, ou étant fonction des coordonnées spatiales et nous devons connaître sa dépendance sur (x, y, z) pour résoudre l'intégrale.

Propriétés

Certaines considérations importantes concernant le centre de masse sont les suivantes:

- Bien qu'un système de référence soit nécessaire pour établir des positions, le centre de masse ne dépend pas du choix qui est fait du système, car il s'agit d'une propriété de l'objet.

- Lorsque l'objet a un axe ou un plan de symétrie, le centre de masse est sur ledit axe ou plan. Profitez de cette circonstance permet un temps de calcul.

- Toutes les forces externes agissant sur l'objet peuvent être appliquées au centre de masse. Suivre la piste de ce point donne une idée globale du mouvement de l'objet et facilite le travail d'étude de son comportement.

-Trouver le centre de gravité d'un corps en équilibre statique

Supposons que le corps de la figure précédente est en équilibre statique.

figure 3. Schéma de calcul du couple de poids par rapport au point ou.

Le moment de la torsion nette par rapport à O, selon la figure 3, est: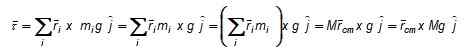Une force F appliquée verticalement au centre de la gravité (ou également au-dessus ou en dessous, sur l'axe qui le traverse) produirait une torsion opposée qui empêcherait la rotation de l'objet et maintiendrait l'équilibre rotationnel. L'ampleur de F est choisie de sorte que l'objet ne soit pas transféré non plus et que nous l'aurons dans l'équilibre statique.

Peut vous servir: optique ondulée

-Exemple résolu

Une mince barre de matériau uniforme a une longueur de 6 m et pèse 30 N. À sa fin, un 50 N à l'ouest et un autre de 20 N à son extrémité droite est pendu. Trouver: a) l'ampleur de la force ascendante nécessaire pour maintenir l'équilibre de la barre, b) le centre de gravité de l'ensemble.

Solution

Le diagramme des forces est illustré dans la figure suivante. Le poids de la barre est appliqué dans son centre de gravité, qui coïncide avec son centre géométrique. La seule dimension de la barre prise en compte est sa longueur, car la déclaration informe qu'elle est mince.

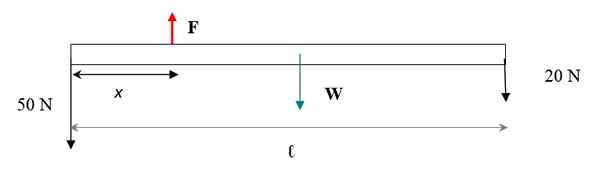Figure 4. Diagramme pàra la barra.

Pour que le système de poids BAR + reste dans l'équilibre de la traduction, la somme des forces doit être nul. Les forces sont verticales, si nous considérons avec un signe + et vers le bas avec un signe - alors:

F- 50 - 20-30 n = 0

F = 100 N

Cette force garantit l'équilibre de la traduction. Prendre les moments de torsion de toutes les forces concernant un axe qui passe par l'extrémité gauche du système et l'application de la définition:

t = r x f

Les moments de toutes ces forces par rapport au point sélectionné sont perpendiculaires au plan de la barre:

t_F = xf = 100x

t_W = - (l / 2) mg = -3m . 30 n = -90 n.m

t₁ = 0 (Puisque la force de 50 N passe par l'axe de virage sélectionné et n'exerce pas de moment)

t₂ = -Lf₂ = 6 m . 20 n = -120 n.m

Donc:

100 x -90 -120 n.m = 0

x = 2.10 m

Le centre de gravité de la barre de barre + poids est situé à 2.10 mètres de l'extrémité gauche de la barre.

Différence avec le centre de masse

Le centre de gravité coïncide avec le centre de masse, comme indiqué, tant que le champ gravitationnel terrestre est constant pour tous les points de l'objet à considérer. Le champ gravitationnel de la Terre n'est rien d'autre que la valeur bien connue et familière de g = 9.8 m / s² réalisé verticalement vers le bas.

Bien que la valeur de G éprouve des variations avec la latitude et l'altitude, elles n'affectent généralement pas les objets dont la plupart du temps est traité. Très différent serait s'il est considéré comme un grand corps à proximité de la terre, par exemple un astéroïde qui près de la planète.

L'astéroïde a son propre centre de masse, mais son centre de gravité n'aurait plus à coïncider avec cela, puisque g Il connaîtrait probablement des variations substantielles d'ampleur, étant donné la taille de l'astéroïde et que les poids de chaque particule peuvent ne pas être parallèles.

Une autre différence fondamentale est que le centre de la masse est qu'il existe ou non une force appelée poids appliqué sur l'objet. Il s'agit d'une propriété intrinsèque de l'objet qui révèle comment sa masse est distribuée par rapport à sa géométrie.

Peut vous servir: quelle est la constante diélectrique?

Le centre de masse existe à la fois s'il y a du poids appliqué comme si. Et est situé dans la même position bien que l'objet soit transféré sur une autre planète dans laquelle le champ gravitationnel est différent.

D'un autre côté, le centre de gravité est clairement lié à l'application du poids, car nous avons pu apprécier tout au long des paragraphes précédents.

Exemples de centre de gravité

Centre de gravité des objets irréguliers

Il est très facile de savoir où le centre de gravité d'un objet irrégulier est comme une tasse. Il est d'abord suspendu de n'importe quel point et à partir de là, une ligne verticale est tracée (dans la figure 5, c'est la ligne fuchsia dans l'image de gauche).

Ensuite, il est suspendu à un autre point et une nouvelle verticale (ligne turquoise dans l'image de droite) est dessinée. L'intersection des deux lignes est le centre de gravité de la tasse.

Figure 5 . CG Emplacement d'une tasse. Source: Pixabay modifié.

Équilibre des objets

Analysons la stabilité d'un camion qui circule le long de la route. Lorsque le centre de gravité est au-dessus de la base du camion, il ne versera pas. L'image de gauche est la position la plus stable.

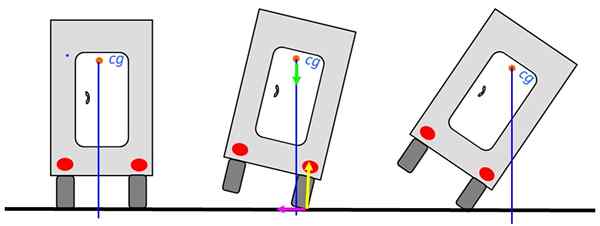Figure 6. Équilibre des camions. Source: auto-faite.

Même lorsque le camion se penche à droite peut revenir à la position d'équilibre stable, comme dans le dessin du milieu, car la verticale passe toujours à travers la base. Cependant, lorsque cette ligne passe à l'extérieur du camion tourne.

Le diagramme montre les forces au point de support: la normale en jaune, le poids en vert et la friction statique à gauche en Fuchsia. NORMAL ET RUBB. Par conséquent, ils ne contribueront pas à vider le camion.

Le poids demeure, qui exerce un moment de torsion, heureusement dans le sens anti-horaire et qui a tendance à retourner dans le camion à sa position d'équilibre. Notez que la ligne verticale passe par la surface de support, qui est le pneu.

Lorsque le camion est en position d'extrême droite, le temps de torsion du poids change et devient dans une direction tendue. Ne pouvant pas être contrecarré à un autre moment, le camion versera.

Les références

1. Bauer, w. 2011. Physique pour l'ingénierie et les sciences. Volume 1. Mc Graw Hill.  247-253.
2. Giancoli, D.  2006. Physique: principes avec applications. 6e ... Ed Prentice Hall. 229-238.
3. Resnick, r. (1999). Physique. Vol. 1. 3e édition. en espagnol. Société de rédaction continentale S.POUR. de c.V. 331-341.
4. Rex, un. 2011. Fondamentaux de la physique. Pearson.146-155.
5. Sears, Zemansky. 2016. Physique universitaire avec physique moderne. 14e. Élégant. Volume 1.340-346.