Types d'axiomes de probabilité, explication, exemples, exercices

Les axiomes de probabilité Ce sont des propositions mathématiques concernant la théorie de la probabilité, qui ne mérite pas la démonstration. Les axiomes ont été créés en 1933 par le mathématicien russe Andrei Kolmogorov (1903-1987) dans son travail Fondamentaux de la théorie des probabilités et a jeté la base de l'étude mathématique de la probabilité.

Lors de la réalisation d'une certaine expérience aléatoire ξ, l'espace d'échantillon est celui avec tous les résultats possibles de l'expérience, également appelée événements. Tout événement est indiqué comme a et p (a) est la probabilité de se produire. Ensuite, Kolmogorov a établi que:

Figure 1. Les axiomes de probabilité permettent de calculer la probabilité de frapper le jeu comme la roulette. Source: Pixabay.

-Axiome 1 (pas de négativité): La probabilité que tout événement se produit est toujours positif ou zéro, P (a) ≥0. Lorsque la probabilité d'un événement est 0, elle s'appelle Événement impossible.

-Axiome 2 (certitude): à condition qu'un événement qui appartient à E, sa probabilité d'occurrence est 1, que nous pouvons exprimer comme P (e) = 1. Est ce qui est connu comme un Événement sûr, Depuis lors de l'exécution d'une expérience, il y a un résultat avec toute certitude.

-Axiome 3 (addition): Dans le cas de deux événements incompatibles ou plus deux à deux, appelés à₁, POUR₂, POUR₃..., la probabilité de l'événement à₁ Plus le A₂ Plus le A₃ Et ainsi de suite, c'est la somme des probabilités que chacun se produit séparément.

Ceci est exprimé comme: P (A₁ U a₂ U a₃ U ...) = p (a₁) + P (a₂) + P (a₃) + ..

Figure 2. Le remarquable mathématicien russe Andrei Kolmogorov (1903-1987), qui a jeté les fondations de la probabilité axiomatique. Source: Wikimedia Commons.

[TOC]

Exemple

Les axiomes de probabilité sont largement utilisés dans de nombreuses applications. Par exemple:

Une griffe ou un tachuela est jeté dans les airs, et lorsque le sol tombe, il y a la possibilité de tomber avec la pointe (u) ou avec la pointe vers le bas (D) (nous ne considérerons pas d'autres possibilités). L'espace d'échantillon de cette expérience se compose de ces événements, alors e = u, d.

Peut vous servir: révolution solides: volume, types, exercices résolusfigure 3. Dans l'expérience du lancement du Tachuela, il y a deux événements de probabilités différentes: tomber avec le bout ou au sol. Source: Pixabay.

En appliquant les axiomes que nous avons:

P (e) = 1 (Axiome 2)

Mais P (e) = p (u) + p (d) (Axiome 3), car ces événements sont mutuellement incompatibles ou disjoints. Le bogue ne tombe pas avec le poinçon ou vers le bas en même temps, il en est l'un ou l'autre, mais pas les deux, car d'autres possibilités sont envisagées. Ensuite:

P (u) + p (d) = 1

P (u) = 1 - p (d)

S'il est également susceptible de tomber avec la pointe ou vers le bas, P (u) = p (d) = ½ (Axiome 1). Cependant, il se peut que ce soit en raison de la construction et de la conception du bug. Par exemple, il se peut que P (u) = ¾ tandis que P (d) = ¼ (Axiome 1).

Notez que dans les deux cas, la somme des probabilités donne 1. Cependant, les axiomes n'indiquent pas comment allouer des probabilités, du moins pas complètement. Mais ils affirment qu'ils sont des nombres entre 0 et 1 et que, comme cela se produit dans ce cas, la somme de tous est 1.

Façons d'attribuer une probabilité

Les axiomes de probabilité ne constituent pas une méthode d'attribution de la valeur de la probabilité. Pour cela, il existe trois options compatibles avec les axiomes:

Règle de Laplace

Chaque événement se voit attribuer la même probabilité de se produire, puis la probabilité d'occurrence est définie comme:

P (a) = nombre de cas favorable à l'événement a / nombre de cas possibles

Par exemple, quelle est la probabilité d'extraire un as d'un jeu de cartes françaises? Le jeu a 52 cartes, 13 de chaque bâton et il y a 4 bâtons. Chaque bâton en a 1, donc au total, il y a 4 as:

P (as) = ​​4/52 = 1/13

La règle de Laplace est limitée aux espaces d'échantillons finis, où chaque événement est tout aussi probable.

Peut vous servir: mathématiques discrètes

Fréquence relative

Ici, l'expérience doit être reproductible, car la méthode est basée sur la réalisation d'un grand nombre de répétitions.

Faisons des répétitions de l'expérience ξ, dont nous constatons que n est le nombre de fois qui se produit un certain événement a, alors la probabilité que cet événement se produise est:

P (a) = lim_{I → ∞} (ni)

Où n / i est la fréquence relative d'un événement.

Définir P (a) de cette manière satisfait les axiomes de Kolmogorov, mais il a la gêne que de nombreux tests doivent être effectués afin que la probabilité soit appropriée.

Méthode subjective

Une personne ou un groupe de personnes peut accepter d'attribuer la probabilité à un événement, par le biais de leurs propres jugements. Cette méthode présente l'inconvénient que différentes personnes peuvent attribuer des probabilités différentes au même événement.

Exercice résolu

Dans l'expérience de lancement simultanément de 3 devises honnêtes, obtenant les chances des événements décrits:

a) 2 visages et une croix.

b) 1 visage et deux croix

c) 3 croix.

d) au moins 1 visage.

Solution à

Les visages sont indiqués avec C et les croix avec x. Mais il y a plusieurs façons d'obtenir deux visages et une croix. Par exemple, les deux premières pièces peuvent tomber avec le visage et le troisième avec Cruz. Ou le premier peut tomber face, la deuxième croix et le troisième visage. Et enfin le premier peut être une croix et les visages restants.

Pour répondre aux questions, il est nécessaire de connaître toutes les possibilités, qui sont décrites dans un outil appelé diagramme d'arbres soit Arbre de probabilités:

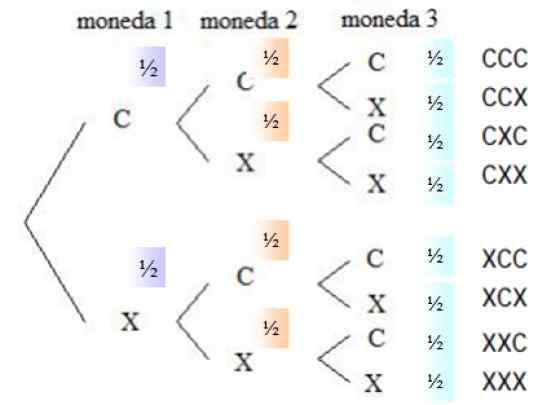Figure 4. Diagramme d'arbres pour le lancement simultané de trois pièces honnêtes. Source: F. Zapata.

La probabilité que dans n'importe quelle devise coûte coûteuse, la même chose se produit pour les croix, car la monnaie est honnête. Dans la colonne de droite, toutes les possibilités de lancement sont répertoriées, c'est-à-dire l'espace d'échantillonnage.

Peut vous servir: variables statistiques

Les combinaisons qui répondent à l'événement demandé sont choisis dans l'espace de l'échantillon, car l'ordre dans lequel les visages apparaissent n'est pas important. Il y a trois événements favorables: CCX, CXC et XCC. La probabilité de chaque événement est:

P (CCX) = ½. ½ . ½ = 1/8

La même chose se produit pour les événements CXC et XCC, chacun a une probabilité de 1/8 de se produire. Par conséquent, la probabilité d'obtenir exactement 2 faces est la somme des probabilités de tous les événements favorables:

P (2 faces) = 1/8 + 1/8 + 1/8 = 3/8 = 0.375

Solution B

Trouver la probabilité qu'il y ait exactement deux croix est un problème analogue à la précédente, il y a également trois événements favorables tirés de l'espace de l'échantillon: CXX, XCX et XXC. Donc:

P (2 croix) = 3/8 = 0.375

Solution C

Sachez intuitivement que la probabilité d'obtenir 3 croix (ou 3 faces) est plus faible. Dans ce cas, l'événement recherché est xxx, à la fin de la colonne de droite, dont la probabilité est:

P (xxx) = ½. ½. ½ = 1/8 = 0.125.

Solution d

Il est demandé d'obtenir au moins 1 visage, cela signifie que 3 faces, 2 faces ou 1 visage peuvent partir. Le seul événement incompatible avec ceci est celui dans lequel 3 croix sortent, dont la probabilité est 0.125. Par conséquent, la probabilité demandée est:

P (au moins 1 face) = 1 - 0.125 = 0.875.

Les références

1. Canavos, g. 1988. Probabilité et statistiques: applications et méthodes. McGraw Hill.
2. Devore, J. 2012. Probabilité et statistiques pour l'ingénierie et la science. 8e. Édition. Cengage.
3. Lipschutz, s. 1991. Série Schaum: probabilité. McGraw Hill.
4. Obregón, je. 1989.Théorie de la probabilité. Limusa éditorial.
5. Walpole, R. 2007. Probabilité et statistiques pour l'ingénierie et la science. Pearson.