Définition de la curtose, types, formules, à quoi sert, par exemple

La Curtose ou kurtosis Il s'agit d'un paramètre statistique qui sert à caractériser la distribution de probabilité d'une variable aléatoire, indiquant le degré de concentration des valeurs autour de la mesure centrale. Ceci est également connu sous le nom de "grade de pointe".

Le terme provient des «kurtos» grecs qui signifie arquée, donc la curtose indique le degré de pointage ou d'aplatissement de la distribution, comme le montre la figure suivante:

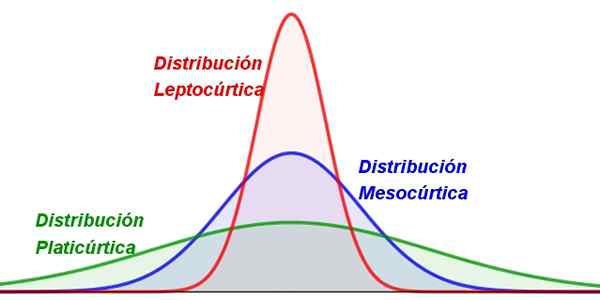Figure 1. Différents types de curtose. Source: F. Zapata.

Presque toutes les valeurs d'une variable aléatoire ont tendance à se regrouper autour d'une valeur centrale telle que la moyenne. Mais dans certaines distributions, les valeurs sont plus dispersées que dans d'autres, résultant en des courbes plus aplaties ou plus minces.

[TOC]

Définition

La curtose est une valeur numérique de chaque distribution de fréquence, qui, selon la concentration des valeurs autour de la moyenne, est classée en trois groupes:

-Leptocuric: dans lequel les valeurs sont très regroupées autour de la moyenne, de sorte que la distribution est assez pointue et mince (figure 1, à gauche).

-Mésocurique: Il a une concentration modérée de valeurs autour de la moyenne (figure 1 au centre).

-Phylicuric: Cette distribution a une forme plus large, car les valeurs ont tendance à être plus dispersées (figure 1 à droite).

Formules et équations

La curtose peut avoir n'importe quelle valeur, sans limites. Son calcul est effectué en fonction de la manière dont les données sont livrées. La notation utilisée dans chaque cas est la suivante:

-Coefficient de cornosis: g₂

-Moyenne arithmétique: X ou X avec barre

-Un i -me: X_Toi

-L'écart type: σ

-Le nombre de données: N

-La fréquence de l'esimo: F_Toi

-Marque de classe: mX_Toi

Avec cette notation, nous présentons certaines des formules les plus couramment utilisées pour trouver la curtose:

Peut vous servir: espace vectoriel: base et dimension, axiomes, propriétés

- Curtose selon la présentation des données

Sans regroupement ou données groupées à des fréquences

Données groupées à intervalles

Excès de curtose

Aussi appelé Coefficient de pointe de Fisher soit Pêcheur, Il sert à comparer la distribution à l'étude avec une distribution normale.

Lorsque l'excès de curtose vaut 0, nous sommes en présence d'une distribution normale ou d'une cloche Gauss. De cette façon, tant que l'excès de bronzage d'une distribution est calculé, nous le comparons en fait à la distribution normale.

À la fois pour les données sans regroupement et pour les données groupées, le coefficient de pointe Fisher, indiqué par K, est:

K = g₂ - 3

Cependant, il peut être démontré que la curtose de la distribution normale est de 3, donc si le coefficient de pointage du Fisher est de 0 ou près de 0 et qu'il y a une distribution mésocurique. Si k> 0, la distribution est leptocurique et si k<0 es platicúrtica.

À quoi sert la curtose pour?

La curtose est une mesure de la variabilité utilisée pour caractériser la morphologie d'une distribution. De cette façon, les distributions symétriques peuvent être comparées à la même moyenne et à une dispersion égale (donnée par l'écart type).

Avoir des mesures de variabilité garantit que les moyennes sont fiables et aident à contrôler les variations de distribution. Par exemple, analysons ces deux situations.

3 départements salaires

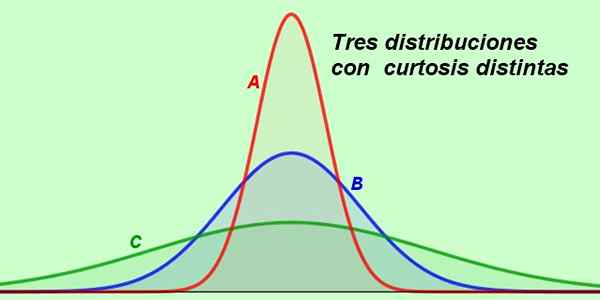
Supposons que le graphique suivant montre les distributions du salaire de 3 départements de la même entreprise:

Figure 2. Trois distributions différentes illustrent des situations pratiques. (Préparé par Fanny Zapata)

La courbe A est la plus mince de toutes, et dans sa forme, il est déduit que la plupart des salaires de ce département sont très proches de la moyenne, donc la plupart des employés reçoivent une compensation similaire.

Peut vous servir: nombres entiers

Pour sa part dans le département B, la courbe de salaire suit une distribution normale, car la courbe est mésocurique, dans laquelle nous supposons que les salaires ont été distribués au hasard.

Et enfin, nous avons la courbe C qui est très aplatie, signe que dans ce département, la gamme de salaire est beaucoup plus large que dans les autres.

Les résultats d'un examen

Supposons maintenant que les trois courbes de la figure 2 représentent les résultats d'un examen appliqué à trois groupes d'étudiants de la même matière.

Le groupe dont les qualifications sont représentées par la courbe vers le leptocuric, est assez homogène, la plus obtenue une note moyenne ou étroite.

Il est également possible que le résultat soit dû au fait que les questions de l'examen avaient plus ou moins le même degré de difficulté.

D'un autre côté, les résultats du groupe C indiquent une plus grande hétérogénéité dans le groupe, qui contient probablement des étudiants moyens, certains étudiants plus exceptionnels et sûrement un autre moins attentif.

Ou cela pourrait signifier que les questions du test avaient des degrés de difficulté très différents.

La courbe B est mésocurique, indiquant que les résultats des tests ont suivi une distribution normale. C'est généralement le cas le plus fréquent.

Exemple résolu de curtose

Trouver le coefficient de pointe de Fisher pour les classes suivantes, obtenues dans un examen de physique à un groupe d'étudiants, avec une échelle de 1 à 10:

5, 5, 4, 7, 7,7, 9, 8, 9, 4, 3

Solution

L'expression suivante sera utilisée pour les données non groupées, données dans les sections précédentes:

Avec le coefficient de ponctual Fisher donné par:

Peut vous servir: Identité pythagorienne: démonstration, exemple, exercices

K = g₂ - 3

Cette valeur permet de connaître le type de distribution.

Pour calculer G₂ Il est pratique de le faire de manière ordonnée, étape par étape, car plusieurs opérations arithmétiques doivent être résolues.

Étape 1

Premièrement, la moyenne des qualifications est calculée. Il y a n = 11 données.

X = (5 + 5 + 4 + 7 + 7 + 7 + 9 + 8 + 9 + 4 + 3) / 11 = 6.182

Étape 2

L'écart type est trouvé, pour lequel cette équation est utilisée:

 En utilisant une calculatrice avec des fonctions statistiques, le résultat est immédiat:

σ = 1.992

Ou vous pouvez également construire un tableau, qui est également requis pour l'étape suivante et dans laquelle chaque terme des résumés qui sera nécessaire est écrit, à commencer par (x_Toi - X), alors (x_Toi - X)² Et puis (x_Toi - X)⁴ :

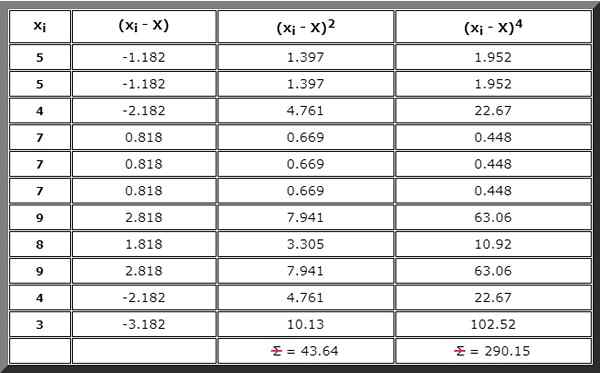
Étape 3

Effectuer la somme indiquée dans le numérateur de formule pour g₂. Pour cela, le résultat de la colonne de droite du tableau précédent est utilisé:

∑ (X_Toi - X)⁴= 290.quinze

Donc:

g₂ = (1/11) x 290.15/1.992⁴ = 1.675

Le coefficient de signalisation de Fisher est:

K = g₂ - 3 = 1.675 - 3 = -1.325

Les intérêts sont le signe du résultat, qui, lorsqu'ils sont négatifs, correspond à une platitud de différents niveaux de difficulté.

L'utilisation d'une feuille de calcul telle que Excel facilite considérablement la résolution de ces types de problèmes et offre également la possibilité de représenter la distribution.

Les références

1. Levin, R. 1988. Statistiques pour les administrateurs. 2e. Édition. Prentice Hall.
2. Marco, F. Curtose. Récupéré de: Economicedia.com.
3. Oliva, J. Asymétrie et curtose. Récupéré de: StatisticsAUCV.Des dossiers.Wordpress.com.
4. Spurr, W. 1982. Prise de décision dans l'administration. Limusa.
5. Wikipédia. Kurtosis. Récupéré de: dans.Wikipédia.org.