Définition et formules moyennes de vitesse angulaire, exercices résolus

La Vitesse angulaire moyenne de rotation est définie comme l'angle tourné par la position de l'unité de temps vectorielle d'un point qui décrit le mouvement circulaire. Les lames d'un ventilateur de plafond (comme celle montrée sur la figure 1), suivent le mouvement circulaire et sa vitesse angulaire moyenne de rotation est calculée en prenant le rapport entre l'angle tourné et le temps dans lequel cet angle a été parcouru.

Les règles suivies du mouvement de rotation sont d'une certaine manière similaire aux parents déjà des parents du mouvement de translation. Les distances parcourues peuvent également être mesurées en mètres, mais les amplitudes angulaires prennent une pertinence particulière car elles facilitent considérablement la description du mouvement.

Figure 1. Les lames de ventilateur ont une vitesse angulaire. Source: Pixabay

Les lettres grecques sont généralement utilisées pour les amplitudes angulaires et les lettres latines pour les amplitudes linéaires correspondantes.

[TOC]

Définition et formules

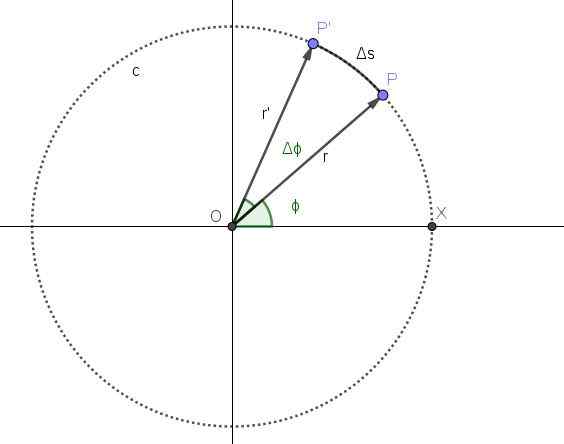
La figure 2 représente le mouvement d'un point sur une trajectoire circulaire C. La position p du point correspond à l'instant t et la position angulaire correspondant à ce moment est ϕ. 

À partir du moment où une période de temps est écoulée Δt. Au cours de cette période, la nouvelle position du point est p 'et la position angulaire a augmenté un angle Δϕ.

Figure 2. Mouvement circulaire d'un point. Source: auto-faite

La vitesse angulaire moyenne ω est l'angle parcouru par unité de temps, de sorte que le quotient Δϕ / Δt représentera la vitesse angulaire moyenne entre les moments t et t + Δt:

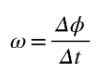
Comme l'angle est mesuré en radians et en temps en secondes, l'unité de la vitesse angulaire moyenne est rad / s. Si vous souhaitez calculer le vitesse angulaire Juste à l'époque t, alors le quotient δϕ / Δt devra être calculé lorsque Δt ➡0.

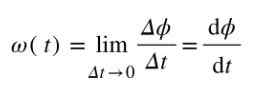L'unité de mesure de la vitesse angulaire instantanée est également rad / s.

Peut vous servir: les 31 types de force en physique et leurs caractéristiques

Rotation uniforme

Un mouvement de rotation est uniforme si à tout moment observé, l'angle parcouru est le même dans la même période. Si la rotation est uniforme, alors la vitesse angulaire coïncide à tout moment avec la vitesse angulaire moyenne.

Dans un mouvement de rotation uniforme, le temps dans lequel un virage complet est appelé période Et il est indiqué avec t. 

De plus, lorsque l'angle parcouru est plein, il est 2π, donc dans une rotation uniforme, la vitesse angulaire ω est liée à la période t, par la formule suivante:

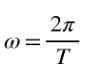
Le fréquence F d'une rotation uniforme comme le rapport entre le nombre de virages et le temps passé à les parcourir, c'est-à-dire, dans le temps Δt, la fréquence sera alors:

F = n / Δt

En tant que tour (n = 1), il est voyagé dans un temps t (la période), la relation suivante est disponible:

F = 1 / t

C'est-à-dire, dans une rotation uniforme, la vitesse angulaire est liée à la fréquence par la relation:

Ω = 2π ・ f

Relation entre la vitesse angulaire et la vitesse linéaire

Vitesse linéaire V, C'est le quotient entre la distance parcourue et la période de temps utilisée pour le déplacer. Dans la figure 2, la distance parcourue est la longueur de l'arc ΔS. 

L'arc ΔS est proportionnel à l'angle parcouru Δϕ et la radio R, remplissant la relation suivante:

ΔS = R ・ Δϕ

Chaque fois que Δϕ est mesuré en radians.

Si nous divisons l'expression précédente entre la période de temps Δt, nous obtiendrons:

(ΔS / ΔT) = R ・ (Δϕ / Δt)

Le premier rapport membre est la vitesse linéaire et le quotient du deuxième membre la vitesse angulaire moyenne:

Peut vous servir: Mount Olympus (Mars)

v = r ・ ω

Exercices résolus

-Exercice 1

Les pointes des lames du ventilateur de toit représentées sur la figure 1 se déplacent avec une vitesse de 5 m / s et les lames sont de 40 cm de rayon.

Avec ces données calculez: i) la vitesse angulaire moyenne de la roue, ii) le nombre de virages que la roue donne en un second, iii) la période en secondes.

Solution 

i) La vitesse linéaire est v = 5 m / s.

La radio est r = 0,40 m.

D'après la relation entre la vitesse linéaire et la vitesse angulaire, nous nettoyons ce dernier:

v = r ・ ω => ω = v / r = (5 m / s) / (0,40 m) = 12,57 rad / s

ii) ω = 2π ・ f => f = ω / 2π = (12,57 rad / s) / (2π rad) = 2 tour / s

iii) t = 1 / f = 1 / (2 tour / s) = 0,5 s par tour.

-Exercice 2

Une promenade de jouets se déplace sur une piste circulaire de rayon de 2 mètres. À 0 s sa position angulaire est 0 rad, mais après un temps t sa position angulaire est

φ (t) = 2 ・ t .

Avec ces données 

i) Calculez la vitesse angulaire moyenne dans les intervalles de temps suivants [0S, 0.5s]; [0.5s, 1.0s]; [1.0, 1.5s] et enfin dans la période [0.0, 1.5s]. 

ii) sur la base des résultats de la partie I) ce qui peut être dit sur le mouvement?

iii) Déterminer la vitesse linéaire moyenne dans la même période de la section I)

iv) Trouvez la vitesse angulaire et la vitesse linéaire pour tout moment.

Solution 

i) La vitesse angulaire moyenne est donnée par la formule suivante:

Nous procédons à calculer l'angle parcouru et la période de temps écoulée dans chaque intervalle.

Intervalle 1: Δϕ = ϕ (0.5s) - ϕ (0.0s) = 2 (rad / s) * 0.5s - 2 (rad / s) * 0.0s = 1.0 rad

                   Δt = 0.5s - 0.0s = 0.5s

Peut vous servir: BTU (unité thermique): équivalences, utilisations, exemples

                   Ω = Δϕ / Δt = 1.0rad / 0.5s = 2.0 rad / s

Intervalle 2: Δϕ = ϕ (1.0S) - ϕ (0.5s) = 2 (rad / s) * 1.0S - 2 (rad / s) * 0.5s = 1.0 rad

                   Δt = 1.0S - 0.5s = 0.5s

                   Ω = Δϕ / Δt = 1.0rad / 0.5s = 2.0 rad / s

Intervalle 3: Δϕ = ϕ (1.5s) - ϕ (1.0s) = 2 (rad / s) * 1.5s - 2 (rad / s) * 1.0s = 1.0 rad

                   Δt = 1.5s - 1.0s = 0.5s

                   Ω = Δϕ / Δt = 1.0rad / 0.5s = 2.0 rad / s

Intervalle 4: Δϕ = ϕ (1.5s) - ϕ (0.0s) = 2 (rad / s) * 1.5s - 2 (rad / s) * 0.0s = 3.0 rad

                   Δt = 1.5s - 0.0s = 1.5s

                   Ω = Δϕ / Δt = 3.0rad / 1.5s = 2.0 rad / s

ii) Compte tenu des résultats précédents, dans lesquels la vitesse angulaire moyenne a été calculée à différents intervalles de temps, le même résultat est toujours obtenu. Il semble indiquer qu'il s'agit d'un mouvement circulaire uniforme. Cependant, ces résultats ne sont pas concluants.

La façon de garantir la conclusion est de calculer la vitesse angulaire moyenne pour un intervalle arbitraire [t, t -t)

                                     Δt = t '- t

                                     Ω = Δϕ / Δt = 2 * (t'-t) / (t'-t) = 2.0 rad / s

Cela signifie que la promenade des jouets a une vitesse angulaire moyenne constante de 2 rad / s dans n'importe quelle période considérée. Mais vous pouvez aller plus loin si la vitesse angulaire instantanée est calculée:

Ceci est interprété comme la voiture jouet en tout temps a une vitesse angulaire constante = 2 rad / s.

Les références

1. Giancoli, D. La physique. Principes avec les applications. 6e édition. Prentice Hall. 30-45.
2. Kirkpatrick, L. 2007. Physique: un regard sur le monde. 6^faire Édition abrégée. Cengage Learning. 117.
3. Resnick, r. (1999). Physique. Volume 1. Troisième édition en espagnol. Mexique. Société de rédaction continentale S.POUR. de c.V. 33-52.
4. SERAY, R., Jewett, J. (2008). Physique pour la science et l'ingénierie. Volume 1. 7e. Édition. Mexique. Cengage Learning Editors. 32-55.
5. Wikipédia. Vitesse angulaire. Récupéré de: Wikipedia.com