Quels sont les vecteurs coplanares? (Avec des exercices résolus)

Les Vecteurs de coplanares o Coplanarios sont ceux qui sont contenus sur le même plan. Lorsque vous n'avez que deux vecteurs, ce sont toujours un couplet.

Si vous avez trois vecteurs ou plus, il se peut que l'un d'eux ne soit pas dans le même plan que les autres, donc ils ne pourraient pas être considérés comme des coplanares. La figure suivante montre un ensemble de coplanares indiqués dans des vecteurs audacieux POUR, B, C et D:

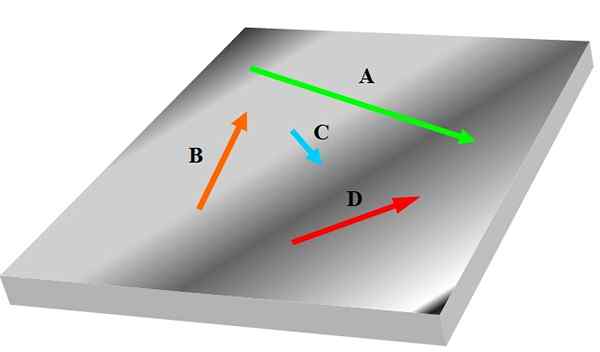Figure 1. Quatre coplanares. Source: auto-faite.

Les vecteurs sont liés au comportement et aux propriétés des amplitudes physiques pertinentes en science et en ingénierie; par exemple la vitesse, l'accélération et la force.

Une force produit des effets différents sur un objet lorsque la façon dont elle est appliquée est variée, par exemple modifier l'intensité, la direction et le sens. Changeant encore l'un de ces paramètres, les résultats sont considérablement différents.

Dans de nombreuses applications, à la fois statiques et dynamiques, les forces qui agissent sur un corps sont sur le même plan, donc elles sont considérées comme des coplanares.

[TOC]

Conditions pour que les vecteurs soient coplanares

Pour que trois vecteurs soient coplanares, ils doivent être sur le même plan et cela se produit s'ils remplissent l'une des conditions suivantes:

-Les vecteurs sont parallèles, donc leurs composants sont proportionnels et dépendent linéairement.

-Votre produit mixte est vide.

-Si vous avez trois vecteurs et que l'un d'eux peut être écrit comme une combinaison linéaire des deux autres, ces vecteurs sont des coplanares. Par exemple un vecteur qui résulte de la somme de deux autres, les trois sont tous dans le même plan.

Peut vous servir: Voltmètre: caractéristiques, fonctionnement, à quoi sert, types

Alternativement, l'état de coplanarité peut être établi comme suit:

U v w Ce sont des coplanares s'il y a trois nombres (scalaires) α, β, γ tels que αou + βV + γW = 0 Avec (α, β, γ) différent de (0, 0, 0)

Produit mixte entre trois vecteurs

Le produit mixte entre les vecteurs est défini avec trois vecteurs ou, V et W, résultant en un scalaire qui résulte de l'exécution de l'opération suivante:

ou · (V X W) = ou · (V X W)

Tout d'abord, le produit croisé entre parenthèses est fabriqué: V X W, dont le résultat est un vecteur normal (perpendiculaire) au plan dans lequel ils sont ainsi V comme W.

Ouais ou est sur le même plan que V et W, Naturellement, le produit scalaire (produit ponctuel) entre u et ledit vecteur normal doit être 0. De cette façon, il est vérifié que les trois vecteurs sont des coplanares (ils se trouvent sur le même plan).

Lorsque le produit mixte n'est pas nulle, son résultat est égal au volume du parallélépipé qui a les vecteurs ou, V et W comme côtés adjacents.

Applications

Coplanares, Forces simultanées et non colinéaires

Les forces concurrent Ils sont tous appliqués sur le même point. S'ils sont également des coplanares, ils peuvent être remplacés par un seul, ce qui est appelé force résultante Et il a le même effet que celui des forces d'origine.

Si un corps est en équilibre grâce à trois coplanares, simultanés et non colinéaires (non parallèles), appelés POUR, B et C, il Théorème de Lamy Il souligne que la relation entre ces forces (amplitudes) est la suivante:

A / sin α = b / sen β = c / sen γ

Avec α, β et γ comme les angles opposés aux forces appliquées, comme le montre la figure suivante:

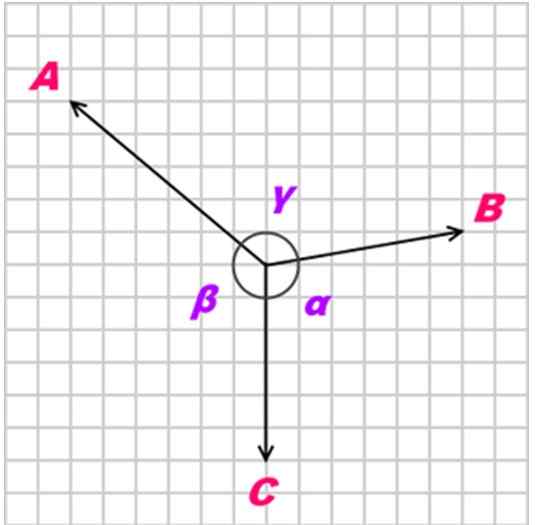Figure 2. Trois forces A, B et C Coplanares agissent sur un objet. Source: Kiwakwok à l'anglais Wikipedia [Domaine public]

Exercices résolus

-Exercice 1

Trouvez la valeur de K pour que les vecteurs suivants soient coplanares:

Peut vous servir: carnot machine

ou =

V =

W =

Solution

Depuis les composants des vecteurs, les critères du produit mixte sont donc utilisés:

ou · (V X W) = 0

Il est résolu d'abord V X W. Les vecteurs seront exprimés en termes de vecteurs unitaires Toi, J et k qui distinguent les trois directions perpendiculaires dans l'espace (large, haut et profondeur):

V= 4 Toi + J + 0 k

W= -1 Toi + 2J -1 k

V X W = -4 (i x i) + 8 (i x j) - 4 (i x k) - (J x i) + 2 (J x J) - 2 (J x k) = 8 k + 4 J + K -2 i = -2 Toi + 4 J + 9 k

Le produit scalaire est maintenant proposé entre U et le vecteur qui a des résultats de l'opération précédente, correspondant à l'opération à 0:

ou · (V X W) = (-3 Toi + k J + 2 k) · (-2 Toi + 4 J + 9 k) = 6 + 4k +18 = 0

24 + 4k = 0

La valeur recherchée est: k = - 6

Pour que le vecteur ou est:

ou =

-Exercer 2

La figure montre un objet dont le poids est w = 600 n, suspendu en équilibre grâce aux câbles placés selon les angles illustrés à la figure 3. Est-il possible d'appliquer le théorème de Lamy dans cette situation? En tout cas trouver les amplitudes de T₁, T₂ et T₃ qui rend l'équilibre possible.

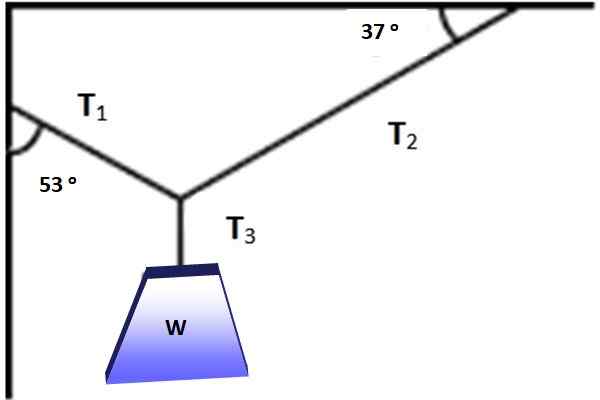figure 3. Un poids est suspendu en équilibre sous l'action des trois tensions indiquées. Source: auto-faite.

Solution

Le théorème de Lamy est applicable dans cette situation si le nœud sur lequel les trois tensions sont appliqués est considéré, car ils constituent un système de forces coplanaires. D'abord, le diagramme du corps libre est conçu pour le poids du pendentif, afin de déterminer l'ampleur de T_3:

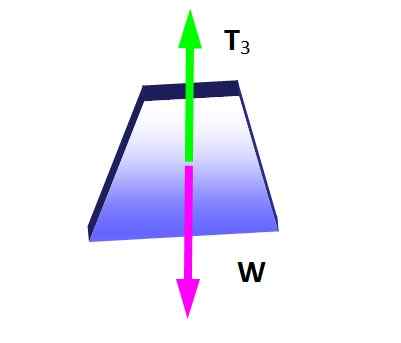Figure 4. Diagramme corporel libre pour le poids suspendu. Source: auto-faite.

De la condition d'équilibre, il s'ensuit que:

Peut vous servir: diffraction du son: ce que sont, des exemples, des applications

T₃  = W = 600 n

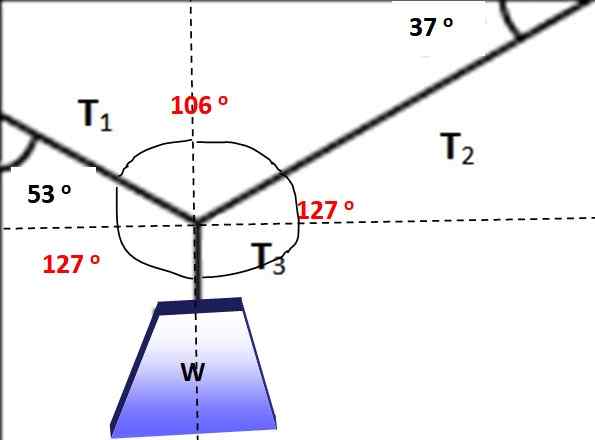
Les angles entre les forces sont marqués en rouge dans la figure suivante, il peut être facilement vérifié que sa somme est à 360 °. Il est désormais possible d'appliquer le théorème de Lamy, car l'une des forces et les trois angles entre eux est connue:

Figure 5.- En rouge les angles pour appliquer le théorème de Lamy. Source: auto-faite.

T₁ / Sen 127º = w / sen 106º

Par conséquent: T₁ = sen 127º (w / sen 106º) = 498.5 N

Encore une fois, le théorème de Lamy est appliqué pour clair t₂:

T₂ / sin 127 = t₁ / Sen 127º

T₂ = T₁ = 498.5 N

Les références

1. Figueroa, D. Série: Physique pour la science et l'ingénierie. Volume 1. Cinématique. 31-68.
2. Physique. Module 8: vecteurs. Récupéré de: Frtl.UTN.Édu.ardente
3. Hibbeler, R. 2006. Mécanique pour les ingénieurs. Statique. 6e édition. Société de rédaction continentale.28-66.
4. McLean, W. Série Schaum. Mécanique pour les ingénieurs: statique et dynamique. 3e édition. McGraw Hill. 1-15.
5. Wikipédia. Vecteur. Récupéré de: c'est.Wikipédia.org.