Mouvement relatif dans une dimension, en deux dimensions, exerce

Il mouvement relatif d'une particule ou d'un objet est celui observé par rapport à un point de référence particulier que l'observateur a choisi, qui peut être fixé ou en mouvement. La vitesse fait toujours référence à un système de coordonnées utilisé pour le décrire.

Par exemple, le CO-Pilote d'une voiture en mouvement et qui se rend confortablement endormi sur son siège est au repos par rapport au conducteur, mais il n'est pas pour un observateur debout sur le trottoir qui voit le passage de la voiture.

Figure 1. Les avions maintiennent une certaine vitesse relative entre eux lors de la pratique des acrobaties. Source: Pixabay.

Alors le mouvement est toujours relatif, mais il arrive que le système de coordonnées ou de référence soit généralement choisi, ayant son origine dans la terre ou le sol, un endroit considéré comme stationnaire. De cette façon, la préoccupation se concentre sur la description du mouvement de l'objet à l'étude.

Est-il possible de décrire la vitesse du co-pilote de sommeil par rapport à un passager voyageant dans une autre voiture? La réponse est oui. Il y a la liberté de choisir la valeur de (x_soit, et_soit, z_soit): L'origine du système de référence. La sélection est arbitraire et dépend de la préférence de l'observateur, ainsi que de la facilité que vous assurez pour la résolution du problème.

[TOC]

Mouvement relatif dans une dimension

Lorsque le mouvement passe le long d'une ligne droite, les mobiles ont des vitesses dans la même direction ou dans la direction opposée, tous deux vus par un observateur debout sur terre (t). L'observateur se déplace-t-il sur les mobiles? Oui, avec la même vitesse qu'ils portent, mais dans la direction opposée.

Comment un mobile se déplace-t-il par rapport à l'autre? Pour découvrir que les vitesses sont ajoutées.

Il peut vous servir: Pluton (planète naine)

-Exemple résolu 1

En référence à la figure indiquée, indiquez la vitesse relative de la voiture 1 par rapport à la voiture 2 dans chaque situation.

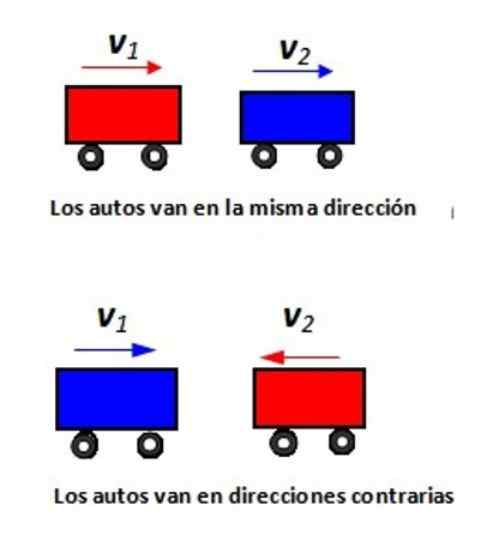Figure 2. Deux voitures vont sur une route rectiligne: a) dans la même direction et b) dans des directions opposées.

Solution

Nous attribuerons un signe positif aux vitesses à droite et un signe négatif à gauche. Si un mobile va à droite à 80 km / h, un passager de ce mobile voit l'observateur au sol se déplacer à 80 km / h.

Supposons que tout se passe le long de l'axe x. Dans la figure suivante, la voiture rouge se déplace à +100 km / h (vu de T) et se prépare à passer la voiture bleue qui se déplace à +80 km / h (également vue à partir de t). Avec quelle vitesse voyez-vous un passager approcher la voiture rouge dans la voiture bleue?

Les étiquettes sont: V _1/2 Auto 1 vitesse par rapport à 2, V_{1 / t} vitesse de voiture par rapport à t, V_{T / 2} Vitesse du tableau par rapport à 2. Ajout de vectoriel:

V_1/2 = V_{1 / t} + V_{T / 2} = (+100 km / h - 80 km / h) X= 20 km / h X

Nous pouvons nous passer de la notation vectorielle. Remarque les indices: multiplier les deux à droite doit obtenir celui à gauche.

Et quand ils sont dans la direction opposée? Maintenant V_{1 / t} = + 80 km / h et V_{2 / t} = -100 km / h, donc V_{T / 2} = + 100 km / h. Le passager du bleu automatique verra la voiture rouge s'approcher:

V_{1/2 =} V_{1 / t} + V_{T / 2} = +80 km / h +100 km / h = 180 km / h

Mouvement relatif en deux et trois dimensions

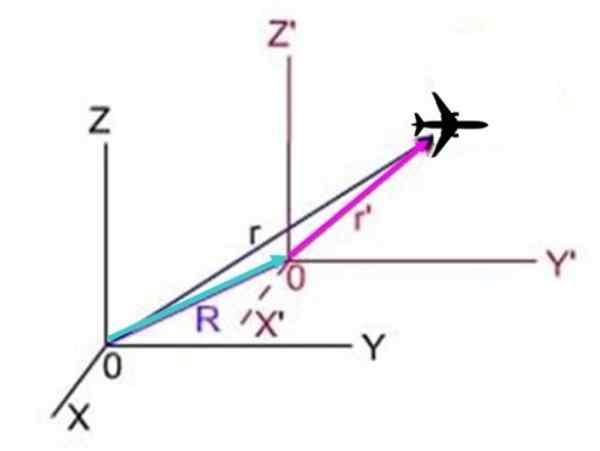
Dans le schéma suivant, r C'est la position de l'avion vu dans le système X y Z, r'C'est la position du système X y Z' et R C'est la position du système avec une prime par rapport au système sans prime. Les trois vecteurs forment un triangle dans lequel R + r'= r, donc r'= r - r.

figure 3.- L'avion se déplace par rapport à deux systèmes de coordonnées, à son tour l'un des systèmes se déplace par rapport à l'autre.

Étant donné que le dérivé par rapport au moment de la position est précisément la vitesse, résultats:

Peut vous servir: photo parabolique: caractéristiques, formules et équations, exemples

V'= V - ou

Dans cette équation V'C'est la vitesse de l'avion par rapport au système X y Z', V est la vitesse par rapport au système X y Z et ou C'est la vitesse constante du système Prime par rapport au système sans primes.

-Exercice résolu 2 

Un avion est dans la direction nord avec une vitesse par rapport à l'air de 240 km / h. Soudain, il commence à souffler le vent de l'ouest en est à une vitesse de 120 km / selon la Terre.

Trouver: a) la vitesse de l'avion par rapport à la terre, b) l'écart subi par le pilote c) la correction que le pilote doit faire pour pouvoir pointer directement vers le nord et la nouvelle vitesse par rapport à la terre, une fois La correction a été apportée.

Solution

a) Les éléments suivants sont eu: plan (a), terre (t) et vent (v).

Dans le système de coordonnées dans lequel le nord est le + et la direction ouest-est est + x il y a les vitesses données et leur étiquette respective (indices):

V _{UN V} = 240 km / h (+et)); V _Vermont = 120 km / h (+X)); V _À = ?

La somme vectorielle adéquate est:

V _À = V _{UN V} + V _Vermont = 240 km / h (+et) + 120 km / h (+X)

L'ampleur de ce vecteur est: V _À = (240 ²+ 120²)^1/2 km / h = 268.3 km / h

b) θ = arctg (v _{UN V} / V _Vermont) = arctg (240/120) = 63.4e au nord de l'Est ou 26.6e nord-est.

c) Pour continuer au nord avec ce vent, vous devez pointer la proue de l'avion au nord-ouest, afin que le vent le pousse directement vers le nord. Dans ce cas, la vitesse de l'avion vue du sol sera dans le + et, bien que la vitesse de l'avion par rapport au vent sera nord-ouest (ce n'est pas nécessairement 26.6e).

Peut vous servir: théorème de Bernoulli

Par Pythagore Theorème:

V _À = (240 ²- 120²)^1/2 km / h = 207.8 km / h

α = arctg (v _Vermont / V _À ) = arctg (120/207.8) = 30e nord-ouest

-Exercice résolu 3

Une personne prend 2 minutes pour descendre un escalier mécanique immobile. Si l'escalier fonctionne, la personne prend 1 minute pour descendre. Combien de temps la personne prend-elle la marche et avec l'escalier en marche?

Solution

Il y a trois éléments à considérer: la personne (p), l'escalier (e) et le (s) sol, dont les vitesses relatives sont:

V_{P / E} : vitesse de la personne par rapport à l'échelle; V_EST: vitesse de l'escalier par rapport au sol; V_{P / s}: Vitesse de la personne par rapport au sol.

Comme on le voit du sol par un observateur fixe, la personne qui abaisse l'escalier (e) a une vitesse V _{P / s} donné par:

V _{P / s} = V_{P / E} + V_EST

Le sens positif est en train de descendre les escaliers. Être t  le temps qu'il faut pour aller marcher et L la distance. L'ampleur de la personne V _{P / s} est:

V_{P / s} = L / T

t₁ C'est le temps qu'il faut pour descendre avec l'échelle arrêtée: V _{P / E} = L / T₁

Et T₂ Celui qui vous emmène toujours sur l'escalier en mouvement: V _EST = L / T₂

Combiner les expressions:

L / t = l / t₁ + L / T₂

Remplacement des valeurs numériques et compensation t:

1 / t = 1 / t₁ + 1 / t₂ = 1/2 + 1/1 = 1.5

Alors t = 1/1.5 minutes = 40 secondes.

Les références

1. Bauer, w. 2011. Physique pour l'ingénierie et les sciences. Volume 1. Mc Graw Hill. 84-88.
2. Figueroa, D. Série physique pour la science et l'ingénierie. Volume 3. Édition. Cinématique. 199-232.
3. Giancoli, D.  2006. Physique: principes avec applications. 6^e. Élégant. Prentice Hall. 62-64.
4. Mouvement relatif. Récupéré de: cours.Lumenarning.com
5. Wilson, J. 2011. Physique 10. Pearson Education. 166-168.