Définition de vitesse angulaire, formule, calcul et exercices

La vitesse angulaire Il s'agit d'une mesure de la vitesse de rotation et est définie comme l'angle qui tourne le vecteur de position de l'objet qui tourne, par unité de temps. C'est une ampleur qui décrit très bien le mouvement de nombreux objets qui se tournent constamment partout: CD, roues de voiture, machines, terre et bien d'autres.

Un schéma du "London Eye" peut être vu dans la figure suivante. Il représente le mouvement d'un passager représenté par le point P, qui suit la trajectoire circulaire, appelée C:

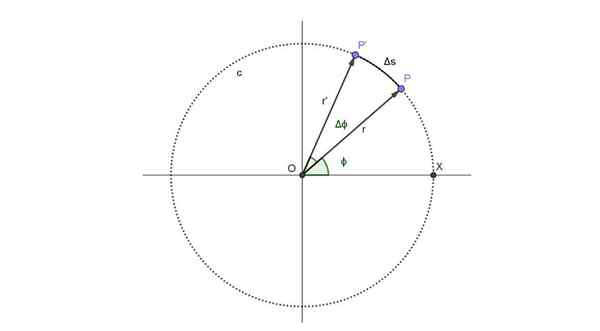Représentation schématique de la trajectoire circulaire qui suit un passager de "l'œil de Londres". Source: auto-faite.

Le passager occupe la position P à l'instant t et la position angulaire correspondant à ce moment est ϕ.

À partir du moment où une période de temps est écoulée Δt. Au cours de cette période, la nouvelle position du passager ponctuel est p 'et la position angulaire a augmenté un angle Δϕ.

[TOC]

Comment la vitesse angulaire est-elle calculée ?

Pour les amplitudes de rotation, les lettres grecques sont largement utilisées, afin de les différencier des amplitudes linéaires. Ainsi, initialement la vitesse angulaire moyenne ω est définie_m Comme l'angle voyageait dans une période donnée.

Alors le quotient Δϕ / Δt représentera la vitesse angulaire moyenne ω_m Parmi les moments t et t + Δt.

Si vous souhaitez calculer le vitesse angulaire Juste au moment t, alors le quotient Δϕ / Δt devra être calculé lorsque Δt ➡0:

 L'unité de mesure de la vitesse angulaire est rad / s.

Relation entre la vitesse linéaire et angulaire

Vitesse linéaire V, C'est le quotient entre la distance parcourue et la période de temps utilisée pour le déplacer.

Dans la figure ci-dessus, la route d'arc est ΔS. Mais cet arc est proportionnel à l'angle parcouru et au rayon, remplissant la relation suivante, qui est valable tant que Δϕ est mesurée en radians:

Peut vous servir: méthode parallélogramme: exemples, exercices résolus

ΔS = R ・ Δϕ

Si nous divisons l'expression précédente entre la période de temps ΔT et prenons la limite lorsque Δt ➡0, nous obtiendrons:

v = r ・ ω

Mouvement de rotation uniforme

La photo est le célèbre «London Eye», une roue rotative de 135 m de haut qui tourne lentement, afin que les gens puissent embarquer sur les cabines à leur base et profiter du paysage de Londres. Source: Pixabay.

Un mouvement de rotation est uniforme si à tout moment observé, l'angle parcouru est le même dans la même période.

Si la rotation est uniforme, alors la vitesse angulaire coïncide à tout moment avec la vitesse angulaire moyenne.

Dans un mouvement de rotation uniforme, le temps dans lequel un virage complet est appelé la période et indique avec t.

De plus, lorsque l'angle est retourné, il est de 2π (équivalent à 360º). C'est pourquoi dans une rotation uniforme, la vitesse angulaire ω est liée à la période t, au moyen de la formule suivante:

La fréquence est définie F d'une rotation uniforme comme le quotient entre le nombre de virages et le temps passé à les parcourir. Comme je reviens, il se déplace dans un temps t (la période) a la relation suivante:

F = 1 / t

En d'autres termes, dans une rotation uniforme, la vitesse angulaire est liée à la fréquence de:

Ω = 2π ・ f

Exercices de vitesse angulaire résolu

Exercice 1

Les cabines de la grande roue rotative connue sous le nom de "Eye de Londres"Ils se déplacent lentement. La vitesse des cabines est de 26 cm / s et la roue mesure 135 m de diamètre.

Avec ces données Calculer:

Peut vous servir: soleil

i) La vitesse angulaire de la roue

ii) la fréquence de rotation

iii) Le temps qui prend une cabine pour faire demi-tour.

Réponses:

Yo) La vitesse v en m / s est: v = 26 cm / s = 0,26 m / s.

La radio est la moitié du diamètre: r = (135 m) / 2 = 67,5 m

v = r ・ ω => ω = v / r = (0,26 m / s) / (67,5 m) = 0,00385 rad / s

Ii) Ω = 2π ・ f => f = ω / 2π = (0,00385 rad / s) / (2π rad) = 6,13 x 10^-4 virages / s

F = 6,13 x 10 ^ -4 tour / s = 0,0368 tour / min = 2,21 tour / heure.

Iii) T = 1 / f = 1/21 tour / heure = 0,45311 Temps = 27 min 11 sec

Exercice 2

Une voiture à jouets se déplace sur une piste circulaire de rayon de 2 mètres. À 0 s, sa position angulaire est 0 rad, mais après un temps t sa position angulaire est donnée par:

φ (t) = 2 ・ t 

Déterminer:

i) vitesse angulaire 

ii) vitesse linéaire à tout moment.

Réponses:

Yo) La vitesse angulaire est la dérivée de la position angulaire: ω = φ '(t) = 2.

Autrement dit.

Ii) La vitesse linéaire de la voiture est: v = r ・ ω = 2 m ・ 2 rad / s = 4 m / s = 14,4 km / h

Exercice 3

La même voiture de l'exercice précédent commence à s'arrêter. Sa position angulaire en fonction du temps est donnée par l'expression suivante:

φ (t) = 2 ・ t - 0,5 ・ t² 

Déterminer:

i) vitesse angulaire à tout moment

ii) vitesse linéaire à tout moment

iii) Le temps que vous prenez pour vous arrêter à partir du moment où vous commencez à décélérer

iv) L'angle parcouru 

v) à distance parcourue

Réponses:

Yo) La vitesse angulaire est la dérivée de la position angulaire: ω = φ '(t)

Ω (t) = φ '(t) = (2 ・ t - 0,5 ・ t²) '= 2 - t

Ii) La vitesse linéaire de la voiture à tout moment est donnée par:

v (t) = r ・ ω (t) = 2 ・ (2 - t) = 4 - 2 t

Peut vous servir: vitesse relative: concept, exemples, exercices

Iii) Le temps qui prend le moment où il commence à ralentir.

v (t) = 4 - 2 t = 0 => t = 2

C'est-à-dire qu'il s'arrête 2 s après avoir commencé à s'arrêter.

Iv) Dans la période de 2s, à partir du moment où il commence à s'arrêter jusqu'à ce qu'un angle donné par φ (2) soit parcouru:

φ (2) = 2 ・ 2 - 0,5 ・ 2 ^ 2 = 4 - 2 = 2 rad = 2 x 180 / π = 114,6 degrés

V) En l'espace de 2 s comprise car il commence à s'arrêter jusqu'à ce qu'il arrête une distance donnée par:

S = r ・ φ = 2m ・ 2 rad = 4 m

Exercice 4

Les roues d'une voiture mesurent 80 cm de diamètre. Si la voiture se déplace à 100 km / h. Trouver: i) la vitesse angulaire de la rotation des roues, ii) la fréquence de rotation des roues, iii) le nombre de tours que la roue donne dans un itinéraire d'une heure.

Réponses:

Yo) En premier lieu, nous allons tourner la vitesse de la voiture de KM / H A M / S

V = 100 km / h = (100/3.6) m / s = 27,78 m / s

La vitesse angulaire de rotation des roues est donnée par:

Ω = v / r = (27,78 m / s) / (0,4 m) = 69,44 rad / s

Ii) La fréquence de rotation des roues est donnée par:

F = ω / 2π = (69,44 rad / s) / (2π rad) = 11,05 tour / s

La fréquence de rotation est généralement exprimée dans les révolutions par minute r.p.m.

F = 11,05 tour / s = 11,05 tour / (1/60) min = 663.15 r.p.m

Iii)  Le nombre de tours que la roue donne dans un itinéraire d'une heure est calculé en sachant que 1 heure = 60 min et que la fréquence est le nombre de tours n divisés par le moment où ces n sont donnés.

F = n / t => n = f ・ t = 663.15 (tournes / min) x 60 min = 39788,7 tours.

Les références

1. Giancoli, D. La physique. Principes avec les applications. 6e édition. Prentice Hall. 106-108.
2. Resnick, r. (1999). Physique. Volume 1. Troisième édition en espagnol. Mexique. Société de rédaction continentale S.POUR. de c.V. 67-69.
3. SERAY, R., Jewett, J. (2008). Physique pour la science et l'ingénierie. Volume 1. 7e. Édition. Mexique. Cengage Learning Editors. 84-85.
4. Géogebra.org