Calcul normal et exemple vecteur

Il Vecteur normal C'est celui qui définit la direction perpendiculaire à une entité géométrique considérée, qui peut être pour une courbe, un plan ou une surface, par exemple.

C'est un concept très utile dans le positionnement d'une particule mobile ou d'une surface dans l'espace. Dans le graphique suivant, il est possible de voir comment le vecteur normal est à une courbe arbitraire C:

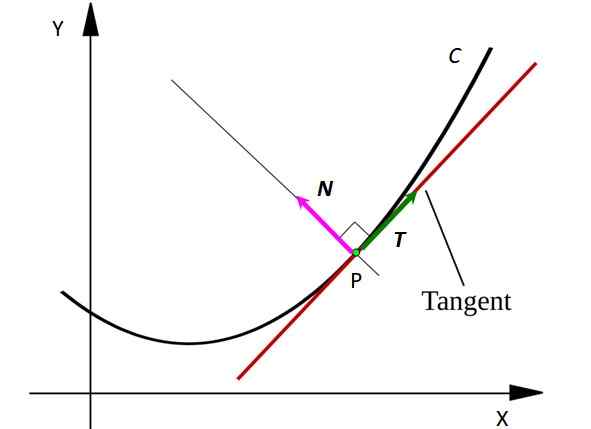
Figure 1. Une courbe C avec le vecteur normal à la courbe au point P. Source: svjo [cc by-sa 3.0 (https: // CreativeCommons.Org / licences / by-sa / 3.0)]

Considérez un point P sur la courbe C. Le point peut représenter une particule mobile qui se déplace après une route en forme de C. La ligne tangente à la courbe au point P apparaît en rouge.

Notez que le vecteur T Il est tangent à C à chaque point, tandis que le vecteur N est perpendiculaire à T et pointe vers le centre d'une circonférence imaginaire dont l'arc est un segment de C. Les vecteurs sont désignés dans une lettre audacieuse dans le texte imprimé, pour les distinguer des autres amplitudes non vectorielles.

Le vecteur T Cela indique toujours où se déplace la particule, il indique donc la vitesse de la même. Au lieu de cela le vecteur N Poignez-vous toujours dans la direction dans laquelle la particule tourne, de cette manière, elle indique la concavité de la courbe C.

[TOC]

Comment amener le vecteur normal dans un avion?

Le vecteur normal n'est pas nécessairement un vecteur unitaire, c'est-à-dire un vecteur dont le module est 1, mais si c'est le cas, il s'appelle vecteur d'unité normal.

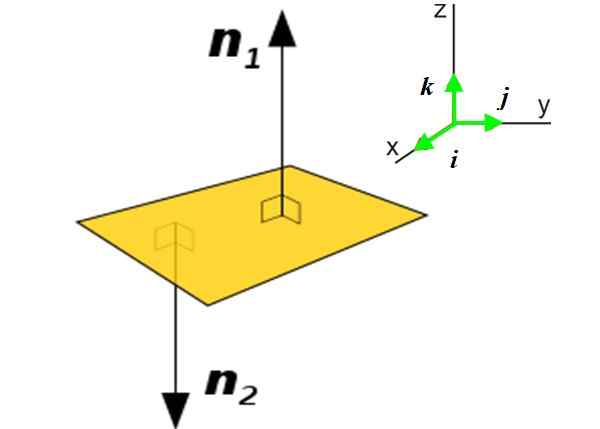Figure 2. À gauche un plan P et les deux vecteurs normaux vers ledit avion. À droite les vecteurs unitaires dans les trois directions qui déterminent l'espace. Source: Wikimedia Commons. Voir page pour l'auteur [Domaine public]

Dans de nombreuses applications, il est nécessaire de connaître le vecteur normal à un avion au lieu d'une courbe. Ce vecteur fait connaître l'orientation dudit avion dans l'espace. Par exemple, considérez l'avion P (jaune) de la figure:

Il peut vous servir: Gemine: origines, caractéristiques et comment les observer

Il y a deux vecteurs normaux dans ce plan: n₁ et n₂. L'utilisation de l'une ou de l'autre dépendra du contexte dans lequel ledit avion est trouvé. L'obtention du vecteur normal dans un plan est très simple si l'équation de celle-ci est connue:

ax + par + cz + d = 0, avec pour, b, c et d nombres réels.

Eh bien, un vecteur plan normal est donné par:

N = A Toi + b J + c k

Ici le vecteur N s'exprime en termes de vecteurs unitaires et perpendiculaire Toi, J et k, dirigé dans les trois directions qui déterminent l'espace X y Z, Voir la figure 2 à droite.

Le vecteur normal du produit vectoriel

Une procédure très simple pour trouver le vecteur normal utilise les propriétés du produit vectoriel entre deux vecteurs.

Comme on le sait, trois points différents et non coménéaux les uns avec les autres, déterminez un plan P. Maintenant, il est possible d'obtenir deux vecteurs ou et V qui appartiennent audit avion ayant ces trois points.

Une fois les vecteurs, le Produit vectoriel ou X V C'est une opération dont le résultat est un vecteur, qui a la propriété d'être perpendiculaire au plan déterminé par ou et V.

Connu ce vecteur, il est désigné comme N, Et à partir de là, il sera possible de déterminer l'équation de l'avion grâce à l'équation indiquée dans la section précédente:

N = ou X V

La figure suivante illustre la procédure décrite:

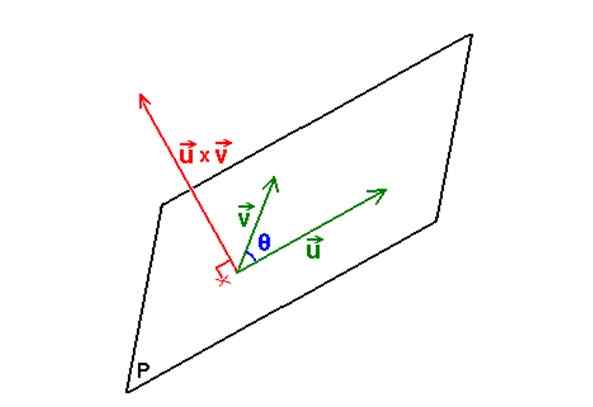figure 3. Avec deux vecteurs et leur vecteur ou produit transversal, l'équation de l'avion contenant les deux vecteurs est déterminée. Source: Wikimedia Commons. Aucun auteur lisible par machine fourni. M.Romero Schmidtke a supposé (sur la base des réclamations du droit d'auteur). [Domaine public]

Exemple

Trouvez l'équation du plan déterminé par les points A (2,1,3); B (0,1,1); C (4,2,1).

Peut vous servir: équation de continuité

Solution

Cet exercice illustre la procédure décrite ci-dessus. En ayant 3 points, l'un d'eux est choisi comme origine commune de deux vecteurs qui appartiennent à l'avion défini par ces points. Par exemple, le point A est défini comme l'origine et les vecteurs sont construits UN B et CA.

Le vecteur UN B C'est le vecteur dont l'origine est le point A et dont la fin est le point B. Coordonnées du vecteur UN B Les coordonnées de B des coordonnées de A:

UN B = (0-2) Toi + (1-1) J + (1-3) k = -2Toi + 0J -2 k

Continuez de la même manière pour trouver le vecteur CA:

CA = (4-2) Toi + (2-1) J + (1-3) k = 2Toi + J -2 k

Calcul du produit vectoriel AB x AC

Il existe plusieurs procédures pour trouver le produit vectoriel entre deux vecteurs. Dans cet exemple, une procédure mnémonique est utilisée qui utilise la figure suivante pour trouver des produits vectoriels parmi les vecteurs unitaires Toi, J et K:

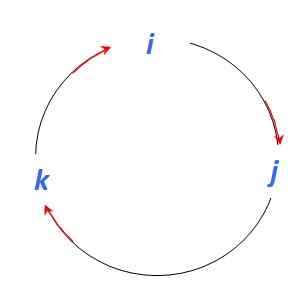Figure 4. Graphique pour déterminer le produit vectoriel entre les vecteurs unitaires. Source: auto-faite.

Pour commencer, il est bon de se rappeler que les produits vectoriels entre les vecteurs parallèles sont donc nul:

Toi X Toi = 0; J X J = 0; k X k = 0

Et comme le produit vectoriel est un autre vecteur perpendiculaire aux vecteurs participants, se déplaçant dans la direction de la flèche rouge que vous avez:

Toi X J = k ; J X k = Toi; k X Toi = J

Si vous devez vous déplacer contraire à la flèche, un signe (-) est ajouté:

J X Toi = - k; k X J = -Toi; Toi X k = -J

Au total, il est possible de fabriquer 9 produits vectoriels avec les vecteurs unitaires Toi, J et k, dont 3 sera nul.

UN B X CA = (-2Toi + 0J -2 k) X (2Toi + J -2 k) = -4 (Toi X Toi) -2 (Toi X J) +4 (Toi X k) +0 (J X Toi) + 0 (J X J) - 0 (J X k) - 4 (k X Toi) -2 (k X J) + 4 (k X k) = -2k-4J-4J+2Toi = 2Toi -8J-2k

Équation plane

Le vecteur n a été déterminé par le produit vectoriel précédemment calculé:

Peut vous servir: mouvement pendulaire

N = 2Toi -8J-2k

Par conséquent, a = 2, b = -8, c = -2, le plan recherché est:

ax + par + cz + d = 0 → 2x-8y-2z + d = 0

La valeur de d. Ceci est facile si les valeurs de l'un des points A, B ou C dont sont disponibles sont remplacés dans l'équation plane. Choisir C par exemple:

x = 4; y = 2; Z = 1

Est laissé:

2.4 - 8.2 - 2.1 + d = 0

-10 + d = 0

D = 10

Bref, l'avion souhaité est:

2x-8y-2z +10 = 0

Le lecteur curieux peut se demander si le même résultat aurait été obtenu si au lieu de faire UN B X CA Il aurait été choisi CA X UN B. La réponse est oui, le plan déterminé par ces trois points est unique et a deux vecteurs normaux, comme le montre la figure 2.

Quant au point sélectionné comme origine des vecteurs, il n'y a également aucun inconvénient à choisir l'un des deux autres.

Les références

1. Figueroa, D. (2005). Série: Physique pour la science et l'ingénierie. Volume 1. Cinématique. Édité par Douglas Figueroa (USB). 31-62.
2. Trouver la normale à un avion. Récupéré de: Web.mame.Utexas.Édu.
3. Larson, R. (1986). Calcul et géométrie analytique. Mc Graw Hill. 616 - 647.
4. Lignes et plans en r 3. Récupéré de: mathématiques.Harvard.Édu.
5. Vecteur normal. Récupéré de Mathworld.Wolfram.com.