Histoire des triangles, éléments, classification, propriétés

Les Triangles Ce sont des figures géométriques plates et fermées, qui se composent de trois côtés. Un triangle est déterminé par trois lignes qui sont coupées de deux à deux, se formant les uns avec les autres trois angles. La forme triangulaire, pleine de symbolisme, est présente dans d'innombrables objets et comme élément de construction.

L'origine du triangle est perdue dans l'histoire. D'après les preuves archéologiques, il est connu que l'humanité primitive le connaissait bien, car les restes archéologiques confirment qu'il a été utilisé dans les outils et les armes.

Figure 1. Triangles. Source: DomainPartures publiques.

Il est également évident que les anciens Égyptiens avaient une solide connaissance de la géométrie et en particulier de la forme triangulaire. Ils étaient incarnés dans les éléments architecturaux de leurs constructions monumentales.

Dans le rhind papyrus, il existe des formules pour le calcul des triangles et des zones de trapèze, ainsi que de certains volumes et autres concepts de trigonométrie rudimentaire.

D'un autre côté, il est connu que les Babyloniens ont pu calculer la zone du triangle et d'autres figures géométriques, qu'ils ont utilisées à des fins pratiques, telles que les divisions du terrain. Ils étaient également conscients de nombreuses propriétés des triangles.

Cependant, ce sont les anciens Grecs qui systématisaient bon nombre des concepts géométriques fréquents aujourd'hui, bien que une grande partie de cette connaissance ne soit pas exclusive, car elle a certainement été partagée avec ces autres civilisations anciennes.

[TOC]

Éléments du triangle

Les éléments de tout triangle sont indiqués dans la figure suivante. Il y en a trois: sommets, côtés et angles.

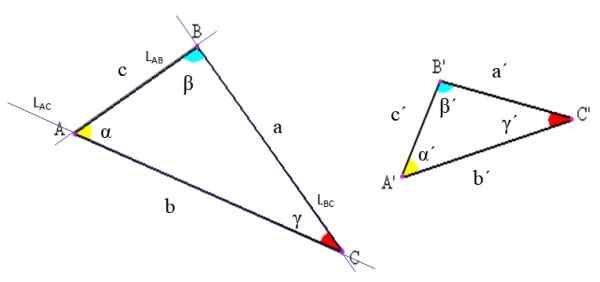Figure 2. Notation des triangles et de leurs éléments. Source: Wikimedia Commons, modifiée par F. Zapata

-Sommets: Ce sont les points d'intersection des lignes dont les segments déterminent le triangle. Dans la figure supérieure par exemple, la ligne L_CA qui contient le segment AC, croise la ligne L_{UN B} qui contient le segment AB juste au point A.

-Côtés: Entre chaque couple de sommets, un segment de ligne est dessiné qui constitue un côté du triangle. Ce segment peut être indiqué avec les lettres des extrémités ou en utilisant une lettre spécifique pour l'appeler. Dans l'exemple de la figure 2, le côté AB est également appelé "C".

-Angle: Entre chaque côté avec un sommet commun, un angle est originaire, dont le sommet coïncide avec celui du triangle. L'angle est généralement indiqué avec une lettre grecque, comme indiqué au début.

Pour construire un triangle particulier, avec une forme et une taille données, disposent de certains des ensembles de données suivants:

-Les trois côtés, assez évidents dans le cas d'un triangle.

-Deux côtés et l'angle entre eux, et le côté restant est immédiatement dessiné.

-Deux angles (internes) et le côté entre eux. Par extension, les deux côtés manquants sont dessinés et le triangle est prêt.

Notation

Généralement, dans la notation des triangles, les conventions suivantes sont utilisées: les sommets sont indiqués par des majuscules, les côtés avec de minuscules lettres latines et les angles par des lettres grecques (voir figure 2).

De cette façon, le triangle est nommé selon ses sommets. Par exemple, le triangle à gauche sur la figure 2 est le triangle ABC, et celui à droite est le triangle a'b'c '.

Il est également possible d'utiliser d'autres notations; Par exemple, l'angle α de la figure 2 est désigné comme BAC. Notez que la lettre du sommet va au milieu et que les lettres sont écrites dans la direction opposée aux aiguilles de l'horloge.

Il peut vous servir: délimitation du problème

D'autres fois, un accent circonflexe est placé pour indiquer l'angle:

Ou le symbole ∠ est utilisé, car la notation précédente peut ne pas être facile en impression, suivie de la lettre correspondant au sommet:

α = ∠a

Types de triangles

Il existe plusieurs critères de classification des triangles. Le plus habituel est de les classer en fonction de la mesure de leurs côtés ou en fonction de la mesure de leurs angles. Selon la mesure de leurs côtés, les triangles peuvent être: scalènes, isocèles ou équilatéraux:

-Scalène: Ses trois côtés sont différents.

-Isocèle: Il a deux côtés différents et un.

-Équilatéral: Les trois côtés sont les mêmes.

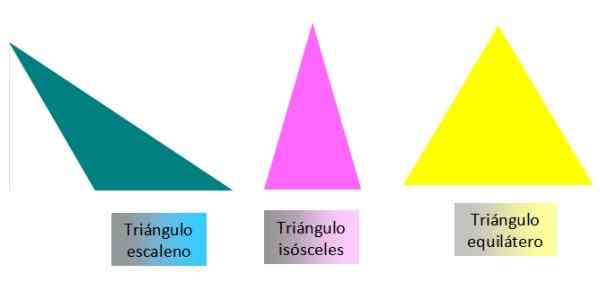figure 3. Classification des triangles de leurs côtés. Source: F. Zapata

Selon la mesure de leurs angles, les triangles sont appelés comme ceci:

-Obtus, Si l'un des angles internes est supérieur à 90º.

-Acutangle, Lorsque les trois angles internes du triangle sont aigus, c'est-à-dire moins de 90º

-Rectangle, Dans le cas où l'un de ses angles internes vaut 90º. Les côtés qui forment 90º sont appelés catetos et le côté opposé à l'angle droit est l'hypoténuse.

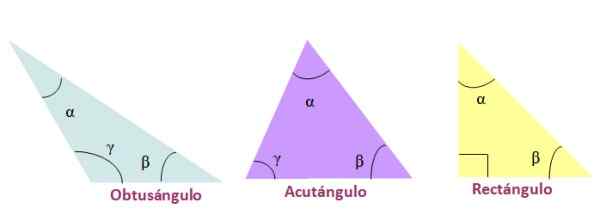Figure 4. Classification des triangles par leurs angles internes. Source: F. Zapata.

Congruence des triangles

Lorsque deux triangles ont la même forme et sont de taille égale, il est dit qu'ils sont congruents. Bien sûr, la congruence est liée à l'égalité, alors pourquoi en géométrie, nous parlons de "deux triangles congruents" au lieu de "deux triangles égaux"?

Eh bien, il est préféré utiliser le terme "congruence" pour s'en tenir à la vérité, car deux triangles peuvent avoir la même forme et la même taille, mais être orientés différemment dans le plan (voir figure 3). Du point de vue de la géométrie, ils ne seraient plus strictement les mêmes.

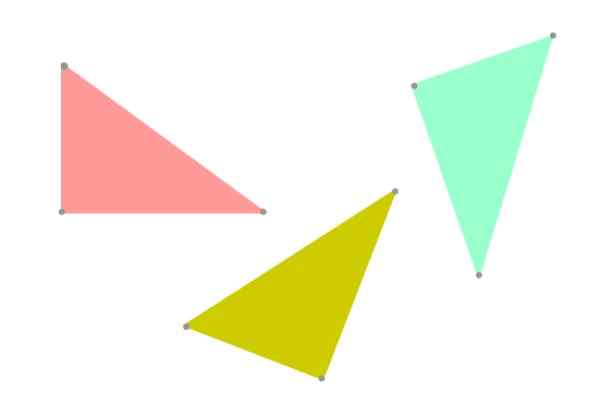Figure 5. Triangles congruents, mais pas nécessairement les mêmes, car son orientation dans le plan est différente. Source: F. Zapata.

Critères de congruence

Deux triangles sont congruents si l'une des situations suivantes se produit:

-Les trois côtés mesurent la même chose (encore une fois, c'est le plus évident).

-Ils ont deux côtés identiques et avec le même angle entre eux.

-Les deux ont deux angles internes identiques et le côté entre ces angles est le même.

Comme on peut le voir, il s'agit que les deux triangles remplissent les conditions nécessaires afin que lors de leur construction, leur forme et leur taille sont exactement les mêmes.

Les critères de congruence sont très utiles, car dans la pratique, d'innombrables pièces et pièces mécaniques doivent être fabriquées en série, de sorte que leurs mesures et leur forme sont exactement les mêmes.

Similitude des triangles

Un triangle est similaire à un autre s'ils ont la même forme, même s'ils sont de taille différente. Pour s'assurer que la forme est la même, il est nécessaire que les angles internes aient la même valeur et que les côtés sont proportionnels.

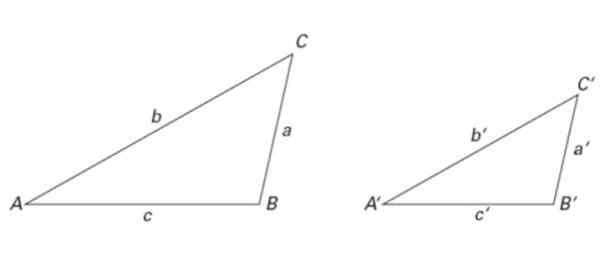Figure 6. Deux triangles similaires: leurs tailles diffèrent mais leurs proportions sont les mêmes. Source: F. Zapata.

Les triangles de la figure 2 sont également similaires, ainsi que ceux de la figure 6. De cette façon:

∠ a = ∠ A ', ∠ B = ∠ B 'et ∠ C = ∠ C '

Quant aux côtés, les raisons suivantes de la similitude sont respectées:

a / a '= b / b' = c / c '

Propriétés

Les propriétés fondamentales des triangles sont les suivantes:

-La somme des angles internes de tout triangle est toujours à 180 °.

-Pour tout triangle, la somme de ses angles externes est égal à 360 °.

Peut vous servir: recherche fondamentale: caractéristiques, définition, exemples

- Un angle externe d'un triangle est égal à la somme des deux angles intérieurs non adjacents à cet angle.

Théorèmes

Premier théorème de tel

Ils sont attribués aux contes de philosophe et de mathématiciennes grecs de miletus, qui ont développé plusieurs théorèmes liés à la géométrie. Le premier d'entre eux établit ce qui suit:

Si plusieurs lignes parallèles coupent deux lignes transversales, elles déterminent les segments proportionnels.

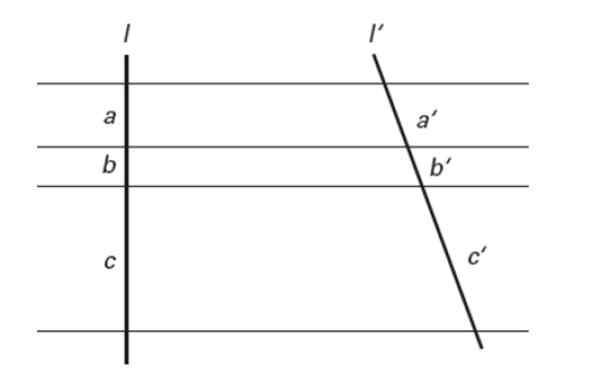Figure 7. Le théorème des contes. Source: F. Zapata.

En d'autres termes:

a / a '= b / b' = c / c '

Le premier théorème de tel est applicable à un triangle, par exemple il y a le triangle Blue ABC à gauche, qui est coupé par les parallèles rouges à droite:

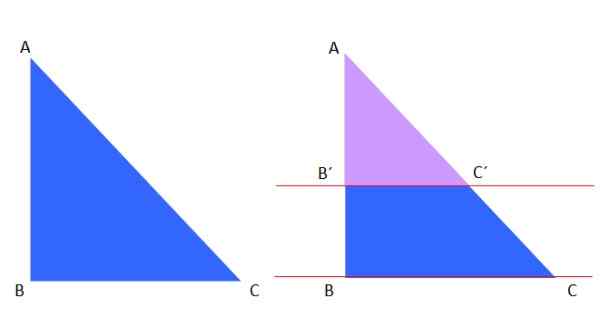Figure 8. Le théorème de tel et des triangles similaires.

Le triangle Violet de Violet est similaire au Triangle Blue ABC, par conséquent, selon ce théorème, ce qui suit peut être écrit:

Ab '/ ac' = ab / ac

Et cela est conforme à ce qui a été expliqué ci-dessus dans le segment de la similitude des triangles. Soit dit en passant, les lignes parallèles peuvent également être verticales ou parallèles à l'hypoténuse et des triangles similaires sont obtenus.

Deuxième théorème de cela

Ce théorème fait également référence à un triangle et à une circonférence centrale ou, comme ceux ci-dessous. Sur cette figure, AC est un diamètre de la circonférence et B en est un point, étant B différent de A et B.

Le deuxième théorème de ces états que:

L'angle entre les segments AB et BC est toujours à 90 °, donc le triangle ABC est un rectangle.

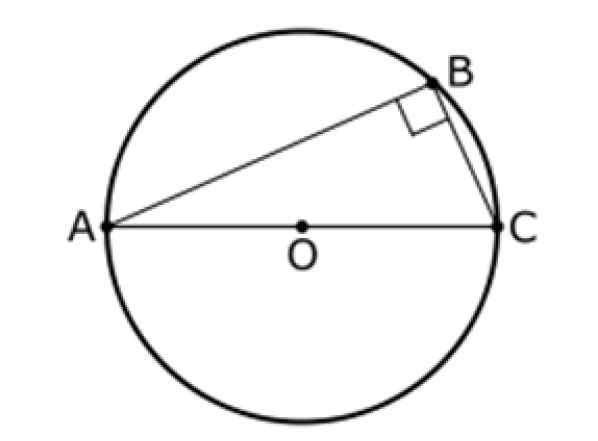Figure 9. Le deuxième théorème de tel. Source: Wikimedia Commons. Inductiveload [domaine public].

Théorème de Pythagore

C'est l'un des théorèmes les plus célèbres de l'histoire. Cela est dû au mathématicien grec Pythagore de Samos (569 - 475 à. C.) et est applicable à un triangle droit. Dit ainsi:

La somme des carrés des longueurs des catégories du triangle rectangle est égale à la longueur de l'hypoténuse haut sur le carré.

Si nous prenons comme exemple le triangle bleu de la figure 8, ou le triangle violet, comme les deux sont des rectangles, alors on peut dire que:

CA² = Ab² + avant JC² (Triangle bleu)

AC '² = Ab '² + AVANT JC '² (Triangle violet)

La zone d'un triangle

La zone du triangle est donnée par le produit de sa base pour et sa hauteur H, divisé par 2. Et par trigonométrie, cette hauteur peut être écrite comme H = b sinθ.

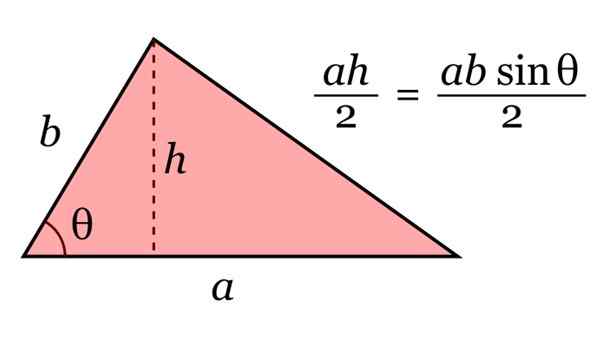Figure 10. Zone du triangle. Source: Wikimedia Commons.

Exemples de triangles

Exemple 1

On dit que grâce à son premier théorème, tel a réussi à mesurer la hauteur de la grande pyramide en Égypte, l'une des 7 merveilles du monde antique, mesurant l'ombre qu'elle a projetée sur le terrain et celle qui projette un pieu coincé dans le sol.

Ceci est le schéma de la procédure suivi de tel:

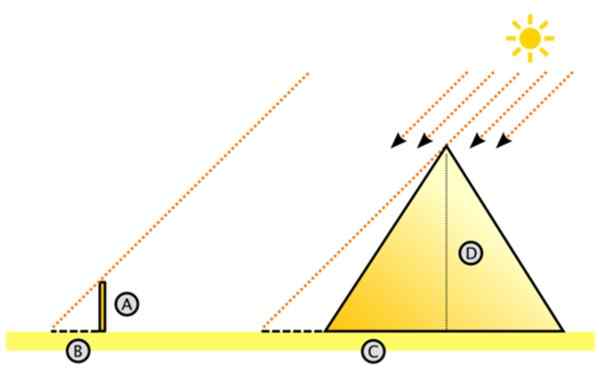Figure 11. Schéma pour mesurer la hauteur de la grande pyramide par la similitude des triangles. Source: Wikimedia Commons. Dake [cc by-sa 3.0 (http: // CreativeCommons.Org / licences / by-sa / 3.0 /]]

Un tel supposé à juste titre que les rayons du soleil affectent le parallèle. Dans cet esprit, il a imaginé le Big Dright Triangle.

Il y a la hauteur de la pyramide et C est la distance sur le sol mesurée du centre à l'ombre projetée par la pyramide sur le sol du désert. Il peut être laborieux de mesurer C, mais il est certainement plus facile que de mesurer la hauteur de la pyramide.

À gauche se trouve le petit triangle, des chats A et B, où A est la hauteur du pieu coincé verticalement sur le sol et B est l'ombre qu'il projette. Les deux longueurs sont mesurables, tout comme c (c est égal à la longueur de l'ombre + la moitié de la longueur de la pyramide).

Peut vous servir: que sont les stimuli tactiles?

Ensuite, par la similitude des triangles:

A / b = d / c

Et la hauteur de la grande pyramide se révèle être: d = c.(UN B)

Exemple 2

Les armures de construction civile sont des structures basées sur des barres droites en bois mince ou en métal, qui sont utilisés comme support dans de nombreux bâtiments. Ils sont également connus sous le nom de réseau, de fermes ou de réticulé (Charpente en anglais).

En eux, les triangles sont toujours présents, car les barres sont interconnectées aux points appelés nœuds, qui peuvent être fixés ou articulés.

Figure 12. Le triangle est présent dans le cadre de ce pont. Source: pxhere.

Exemple 3

La méthode connue sous le nom de triangulation vous permet d'obtenir l'emplacement de points inaccessibles en connaissant d'autres distances plus faciles à mesurer, à condition qu'un triangle se forme qui comprend parmi ses sommets l'emplacement souhaité.

Par exemple, dans la figure suivante, vous voulez savoir à quel moment la mer est le navire, indiqué comme b.

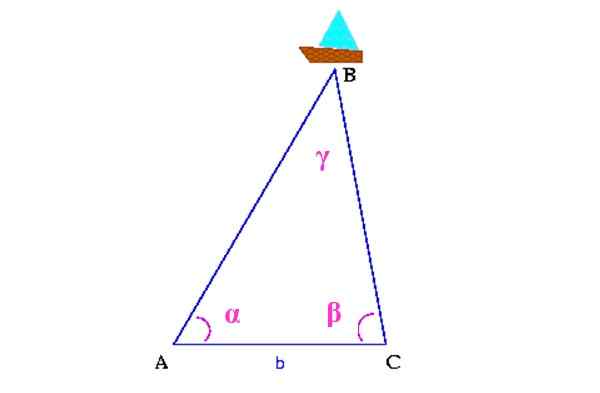Figure 13. Schéma de triangulation pour localiser le navire. Source: Wikimedia Commons. Colette [CC BY-SA 3.0 (http: // CreativeCommons.Org / licences / by-sa / 3.0 /]]

Premièrement, la distance entre deux points sur la côte est mesurée, qui sur la figure est a et c. Alors vous devez déterminer les angles α et β, à l'aide d'un théodolite, Un appareil qui sert à mesurer les angles verticaux et horizontaux.

Avec toutes ces informations, un triangle est construit sur le sommet supérieur duquel est le navire. Cela réduirait l'angle γ, par des moyens.

Exercices

Exercice 1

Dans la figure montrée, les rayons du soleil sont parallèles. De cette façon, l'arbre High à 5 mètres projette une ombre de 6 mètres au sol. En même temps, l'ombre du bâtiment est de 40 mètres. Suivant un tel théorème de tel, trouvez la hauteur du bâtiment.

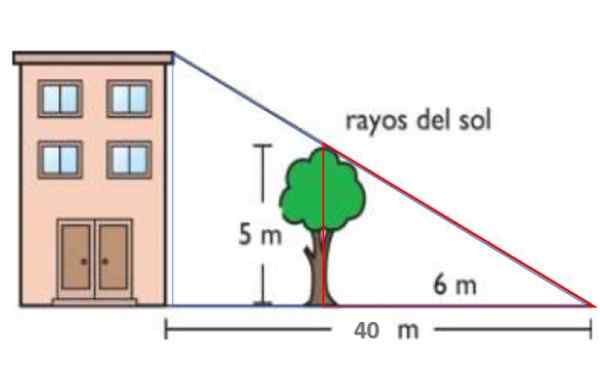Figure 14. Le régime pour l'année résolu 1. Source: F. Zapata.

Solution

Le triangle rouge a des côtés de 5 et 6 mètres respectivement, tandis que le bleu a une hauteur h - la hauteur du bâtiment et de la base de 40 mètres. Les deux triangles sont donc similaires:

H / 40 = 5/6 → h = 40.(5/6) M = 33.3 m

Exercice 2

Vous devez connaître la distance horizontale entre deux points POUR et B, Mais ils sont situés sur un terrain très irrégulier.

À peu près au milieu (p_m) De cette terre, une importance de 1 se démarque.75 mètres de haut. Si le ruban à mesurer indique 26 mètres de longueur mesuré de A à l'importance et à 27 mètres de B au même point, trouvez la distance UN B.

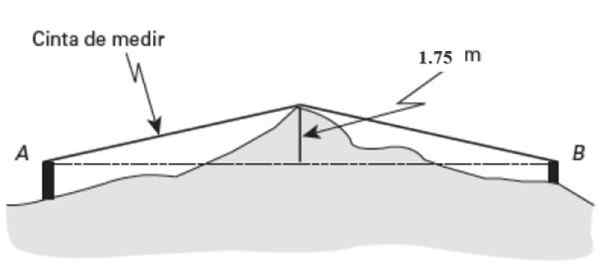Figure 15. Le schéma pour l'exercice a résolu 2. Source: Jiménez, R. Mathématiques II. Géométrie et trigonométrie.

Solution

Le théorème de Pythagore est appliqué à l'un des deux triangles de rectangles de la figure. En commençant par celui de gauche:

Hypoténuse = c = 26 mètres

Hauteur = a = 1.75 mètres

AP_m = (26² - 1.75²)^1/2 = 25.94 m

Maintenant, Pythagore est appliqué dans le triangle droit, cette fois c = 27 mètres, a = 1.75 mètres. Avec ces valeurs:

Bp_m= (27² - 1.75²)^1/2 = 26.94 m

La distance AB ajoute ces résultats:

Ab = 25.94 m +26.94 M = 52.88 m.

Les références

1. Baldor, J. POUR. 1973.Géométrie plate et espace. Culturel d'Amérique centrale.
2. Barredo, D. La géométrie du triangle. Récupéré de: ficus.pntique.MEC.est.
3. Jiménez, R. 2010. Mathématiques II. Géométrie et trigonométrie. Deuxième édition. Pearson.
4. Wentworth, G. Géométrie de la planète. Récupéré de: Gutenberg.org.
5. Wikipédia. Triangle. Récupéré de: est. Wikipédia.org.