Triangle obtus

Nous expliquons ce qu'est un triangle obtus, ses éléments, ses caractéristiques, ses types, ses exemples et un exercice résolu

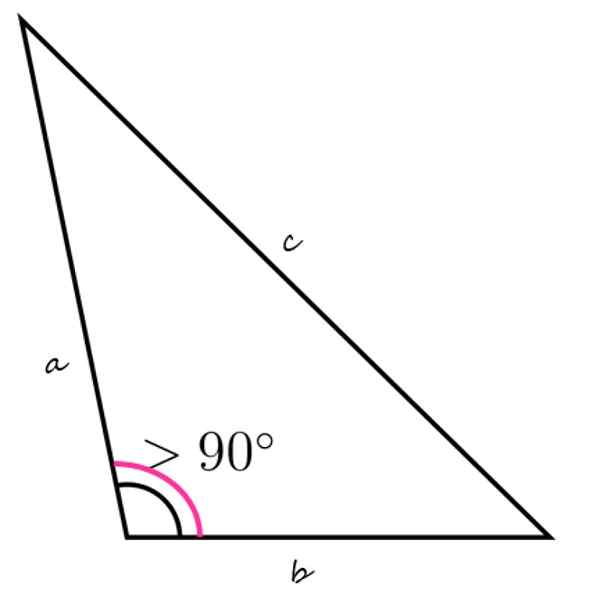Le triangle obtus est caractérisé par un angle interne supérieur à 90º

Qu'est-ce qu'un triangle obtus?

UN triangle obtus C'est la figure plate, fermée et avec trois côtés, qui contient également un angle interne obtus, c'est-à-dire supérieur à 90 ° et moins de 180º.

Tout triangle contient 3 angles internes, et si l'un d'eux est obtus, les deux autres sont, par force, aiguës, car la somme des angles internes de tout triangle est toujours égal à 180º.

La figure supérieure montre un exemple de triangle obtus, avec l'angle interne inférieur gauche supérieur à 90º. Les angles internes restants doivent ajouter moins de 90 °, seulement de cette manière est vrai que la somme des trois est égale à 180º.

En plus des triangles obtus, il y a des triangles acutangulaires, si tous ses angles internes sont aigus et des triangles rectangulaires, lorsque l'un des angles internes mesure exactement 90 °.

Éléments des triangles obtus

Les triangles obtusángulos ont les éléments communs à tous les triangles: ce sont des figures plates à 3 faces, avec 3 angles internes et 3 sommets. De plus, ils ont des segments notables, appelés Ceviens, comme la hauteur, la médiane et le médian et les points où les ceviens se croisent.

Chacun de ces éléments est brièvement défini comme suit:

-Côtés, sont les segments qui composent la figure.

-Sommets, points d'intersection de chaque couple de côtés adjacents.

-Angles internes, Ils se trouvent entre deux côtés adjacents, sur le côté intérieur de la figure, coïncidant le sommet de l'angle avec celui du triangle.

-Angles externes, Ils sont entre un côté et l'extension du côté adjacent, à l'extérieur de la figure, le sommet étant commun, à la fois du triangle et de l'angle. La somme de la mesure entre l'angle interne et son angle adjacent externe est de 180 °, de sorte qu'ils sont des angles complémentaires.

Il peut vous servir: Test de Tukey: qu'est-ce que, en cas d'exemple, un exercice résolu

-Hauteur, C'est la mesure du segment perpendiculaire qui rejoint un sommet avec le côté opposé, ou avec l'extension de ce.

-Médian, ligne dirigée d'un sommet au centre du côté opposé.

-Médiatrice, segment perpendiculaire sur le côté et qui passe juste à travers son centre.

-Bissecteur, C'est un segment qui se divise par un demi-angle interne du triangle.

-Orocentro, point d'intersection des trois hauteurs.

-Barycenter, Aussi appelé centroïde, c'est le point où les trois médianes se croisent.

-Circoncentro, Ici, les trois médias sont coupés.

-Au centre, Point de confluence des bissecteurs.

Une fois ces concepts examinés, certaines des caractéristiques les plus notables des triangles obtuses sont décrites ci-dessous.

Caractéristiques

1.- La somme des trois angles internes du triangle obtus est de 180 °, par conséquent, un seul de ses angles internes peut être supérieur à 90 °, tandis que la somme des deux autres est inférieure à 90º.

2.- Le côté le plus long du triangle obtus est opposé à l'angle obtus.

3.- Dans un triangle obtus, les hauteurs des sommets qui font un angle aigu, traversent les extensions des côtés opposés.

4.- L'orthocentre d'un triangle obtus est hors de la figure.

5.- Le circoncentro du triangle obtus tombe également du triangle (cela ne se produit pas avec le triangle Acutangle).

6.- Il est seulement possible d'enregistrer un carré dans le triangle obtus, soutenant l'un des côtés du carré du côté le plus long du triangle. Deux carrés peuvent être dessinés, soutenant le côté sur les côtés les plus courts du triangle, laissant un sommet non enregistré (ce qui ne touche pas le côté du triangle).

Peut vous servir: Tidecágono

7.- Être un triangle obtus de côtés (a, b, c), étant c le côté le plus long. L'inégalité suivante est valable:

pour²+b² < c²

8.- Ce sont deux triangles obtus, dont les côtés respectifs sont (a, b, c) et (u, v, w). Les côtés les plus longs de chacun sont C et W, de sorte que l'inégalité suivante est réalisée:

A ∙ U + B ∙ V < c∙w

Types de triangles entravés

Les triangles obtus peuvent être de deux types, selon la longueur de leurs côtés:

• Isocèle
• Scalène

Ils sont brièvement décrits ci-dessous:

Triangle isocèle

C'est celui qui a deux côtés égaux et un autre, c'est-à-dire que ses côtés sont (a, a, c).

Lorsque le triangle isocèle est à la fois obtus, les côtés de la mesure «A» sont plus courts et le côté «C» est le plus long. L'angle obtus est formé entre les mêmes côtés, tandis que les deux angles aigus sont de mesure égale et se forment entre les côtés "A" et le côté "C".

Et comme indiqué dans la section précédente, côté "C", car c'est le plus long, il est opposé à l'angle obtus.

Triangle scalène

Les trois côtés du triangle scalène ont une mesure différente: (a, b, c).

Exemples

Exemple 1

Le triangle illustré dans la figure suivante est obtus. L'angle obtus est γ = 114.5e et il est vérifié que la somme des trois angles internes est de 180º:

114.5e + 36.8º + 28.6e ≈ 180º

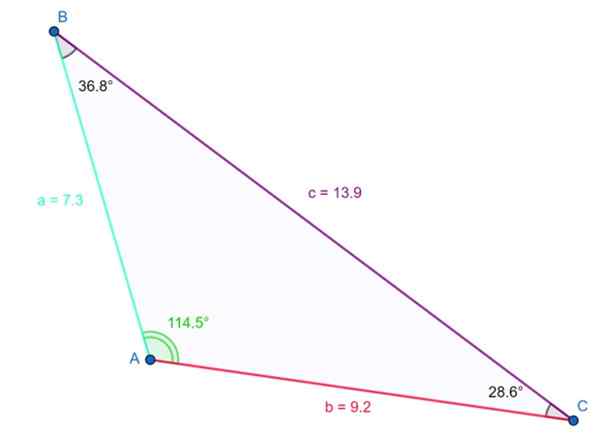Exemple de triangle obtus. Source: F. Zapata

Le côté le plus long mesure 13.9 unités et s'oppose à l'angle obtus. L'inégalité susmentionnée est également atteinte:

pour²+b² < c²

Peut vous servir: Relations de proportionnalité: concept, exemples et exercices

Oui a = 7.3 et b = 9.2, alors:

7.3² + 9.2² < 13.9²

137.93 < 193.2

Exemple 2

Dans le triangle Calabi, il est possible de placer le plus grand carré possible, de trois manières différentes dans le triangle, comme le montre la figure suivante.

Le triangle de Calabi est isocèle et obtus. L'angle obtus est d'environ 101.736 ° et angles aigus à la mesure de base à la fois 39.13e, aussi approximativement.

Exercice résolu

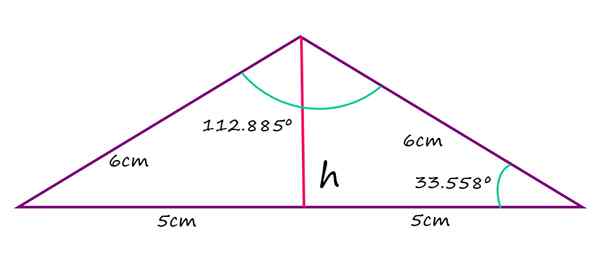
Les côtés égaux d'un triangle isocèle obtus mesure 6 cm, tandis que le côté le plus long mesure 10 cm. Calculez la valeur de l'angle obtus, celle des angles Agudos restants et la hauteur dudit sommet à la base.

Solution

Le théorème du cosinus peut être utilisé pour trouver le cosinus de l'angle obtus. Ensuite, à l'aide de la calculatrice, l'angle en question est déterminé, indiqué γ.

Le théorème de Coseno déclare que:

c² = A² +b² - 2ab ∙ cos γ

Où γ est l'angle entre les côtés A et B. Comme le triangle est isocèle, les côtés A et B sont donc les mêmes:

c² = 2A² - 2e²∙ cos γ

Effacer Cos γ:

 L'angle obtus est l'arc -0 cosinus.38889, qui est environ 112.885º. La valeur de α, l'angle aigu formé par les côtés de 6 cm avec les 10 cm est:

2α + 112.885º = 180º

α = (180 - 112.885) / 2 = 33.558º

Triangle isocèle obtus. Source: F. Zapata

Quant à la hauteur du triangle, mesurée à partir de la base, il est obtenu en observant que cette hauteur divise le triangle en deux rectangles égaux, avec de l'hypotenusa égal à 6 cm et 5 cm de base. Dans un tel cas, le théorème de Pythagore s'applique pour trouver directement la valeur de H: