Caractéristiques de trajectoire physique, types, exemples et exercices

La Trajectoire en physique C'est la courbe qui décrit un mobile lorsqu'il passe par des points successifs pendant son mouvement. Comme cela peut adopter d'innombrables variantes, ils seront également les trajectoires que le mobile peut suivre.

Pour aller d'un endroit à un autre, une personne peut emprunter différentes chemins et différentes manières: à pied à travers les trottoirs dans les rues et les avenues, ou arriver en voiture ou en moto sur une autoroute. Lors d'une balade à travers la forêt, le marcheur peut suivre une trajectoire compliquée qui comprend des virages, de l'escalade ou de la chute et jusqu'à ce qu'il passe plusieurs fois par le même point.

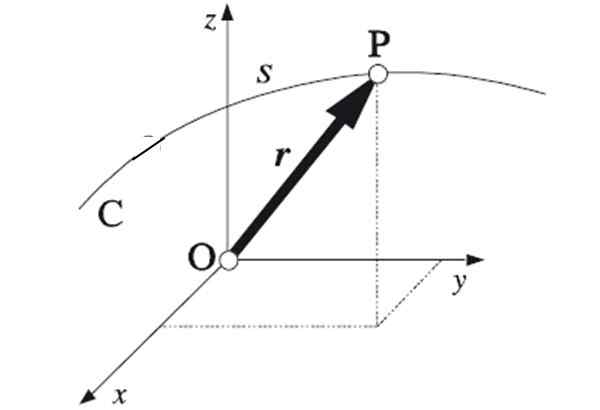Figure 1. Rejoignant les points extrêmes de chaque vecteur de position, la trajectoire suivie de la particule est obtenue. Source: Algarabia [domaine public]

Si les points par lesquels le mobile se déplace suit une ligne droite, la trajectoire sera rectiligne. C'est la trajectoire la plus simple, pour être une dimension. La spécification de la position nécessite une seule coordonnée.

Mais le mobile peut suivre une trajectoire curvyl, pouvoir être fermé ou ouvert. Dans ces cas, la surveillance de la position nécessite deux ou trois coordonnées. Ce sont des mouvements dans le plan et l'espace respectivement. Cela a à voir avec des liens: Limiter les conditions matérielles du mouvement. Certains exemples sont:

- Les orbites qui décrivent les planètes autour du soleil sont des trajectoires en forme d'ellipse fermées. Bien que, dans certains cas, ils puissent se rapprocher d'une circulaire, comme dans le cas de la Terre.

- Le ballon que le gardien de but donne un coup de pied à un but suit une trajectoire parabolique.

- Un oiseau en vol décrit les trajectoires curvilignes dans l'espace, car en plus de se déplacer sur un avion, il peut augmenter ou inférieur à volonté.

La trajectoire physique peut être exprimée mathématiquement lorsque la position mobile est connue à tout moment de. Être r Le vecteur de position, qui à son tour a coordonné X, et et z Dans le cas le plus général d'un mouvement à trois dimensions. Connaître la fonction r (T) La trajectoire sera complètement déterminée.

[TOC]

Gars

En termes généraux, la trajectoire peut être une courbe assez compliquée, surtout si vous voulez exprimer mathématiquement. Par conséquent, il commence par les modèles les plus simples, où les mobiles voyagent sur une ligne droite ou dans un avion, qui peut être le sol ou tout autre approprié:

Mouvements en une, deux et trois dimensions

Les trajectoires les plus étudiées sont:

- Rectiligne, Lorsque vous voyagez sur une ligne horizontale, verticale ou inclinée. Une balle lancée verticalement vers le haut de cette trajectoire ou d'un objet qui se glisse également par un plan incliné. Ce sont des mouvements d'une seule dimension, une seule coordonnée est suffisante pour déterminer complètement sa position.

- Parabolique, dans lequel le mobile décrit un arc parabole. Il est fréquent, car tout objet lancé obliquement sous l'action de la gravité (un projectile) suit cette trajectoire. Pour spécifier la position mobile, vous devez donner deux coordonnées: X et et.

- Circulaire, se produit lorsque la particule en mouvement suit une circonférence. Il est également de nature courante et de pratique quotidienne. De nombreux objets de tous les jours suivent une trajectoire circulaire telle que des pneus, des morceaux de machines et des satellites en orbite, pour donner quelques exemples.

Peut vous servir: vecteurs équipocent: définition, notation, exercices

- Elliptique, L'objet se déplace après une ellipse. Comme indiqué au début, c'est la trajectoire que les planètes suivent en orbite autour du soleil.

- Hyperbolique, Les objets astronomiques sous l'action d'une force centrale (gravité), peuvent suivre les trajectoires elliptiques (fermées) ou hyperboliques (ouvertes), celles-ci étant moins fréquentes que la première.

- Hélicoïdal, o Mouvement en spirale, comme celui d'un oiseau qui monte dans un courant thermique.

- Balancement ou pendulaire, Le mobile décrit un arc dans les mouvements aller-retour.

Exemples

Les trajectoires décrites dans la section précédente sont très utiles pour avoir rapidement une idée de la façon dont les mouvements d'un objet sont. Dans tous les cas, il est nécessaire de préciser que la trajectoire d'un mobile dépend de l'emplacement de l'observateur. Cela signifie que le même événement peut être vu de différentes manières, selon où chacun est.

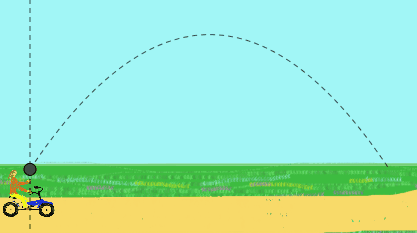
Par exemple, une pédale de filles à vitesse constante et lance une balle. Elle observe que la balle décrit une trajectoire rectiligne. 

Cependant, pour un observateur debout sur la route qui le voit, le ballon aura un mouvement parabolique. Pour lui, le ballon a été initialement lancé à une vitesse inclinée, le résultat de la vitesse de la main de la fille plus la vitesse du vélo.

Figure 2. Cette animation montre le lancement vertical d'une balle faite par une fille qui va à vélo, comme elle le voit (trajectoire rectiligne) et comme vous le voyez un observateur (trajectoire parabolique). (Préparé par f. Zapata).

Trajectoire d'un mobile d'une manière explicite, implicite et paramétrique

- Explicite, spécifiant directement la courbe ou le lieu géométrique donné par l'équation et (x)

- Implicite, dans lequel une courbe est exprimée comme f (x, y, z) = 0

-Paramétrique, De cette façon, les coordonnées x et y z se produisent en fonction d'un paramètre qui, en général, est choisi comme temps t. Dans ce cas, la trajectoire se compose des fonctions: x (t), et T) et z (t).

Ensuite, deux trajectoires très étudiées sont détaillées en cinéma: la trajectoire parabolique et la trajectoire circulaire.

Lancement dans un vide

Un objet (le projectile) est jeté en formant un angle a avec l'horizontal et avec une vitesse initiale V_soit Comme le montre l'image. La résistance à l'air n'est pas prise en compte. Le mouvement peut être traité comme deux mouvements indépendants et simultanés: un horizontal avec une vitesse constante et une autre vitesse verticale sous l'action de la gravité.

x (t) = x_soit +V_bœuf.t

et (t) = y_soit +V_Oy.T -½g.t²

Ces équations sont équations paramétriques du lancement de projectile. Comme expliqué ci-dessus, ils ont un paramètre commun t, quel est le temps.

Dans le triangle de droite de la figure, on peut le voir suivant:

V_bœuf = V_soit cos θ_Toi

V_Oy = V_soit sin θ_Toi

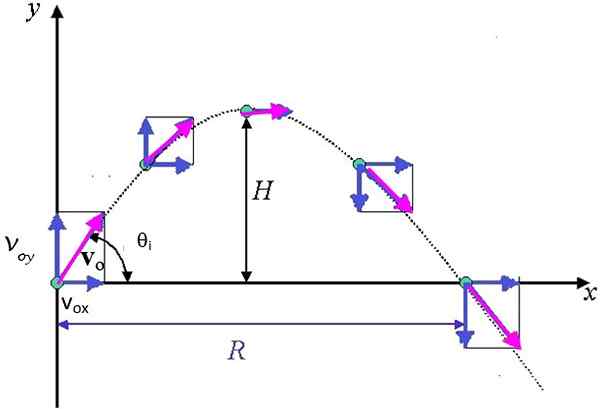figure 3. Trajectoire parabolique suivie d'un projectile, qui montre les composants du vecteur de vitesse. H est la hauteur maximale et r est la portée horizontale maximale. Source: Ayush12Gupta [CC BY-SA 4.0 (https: // CreativeCommons.Org / licences / by-sa / 4.0)]

En remplaçant ces équations qui contiennent l'angle de lancement dans les équations paramétriques, c'est:

Peut vous servir: diffraction du son: ce que sont, des exemples, des applications

x (t) = x_soit +V_soit cos θ_Toi.t

et (t) = y_soit +V_soit. sin θ_Toi.T -½g.t²

Équation de trajectoire parabolique

L'équation explicite de la trajectoire efface t de l'équation pour x (t) et remplace dans l'équation y (t) (t). Pour faciliter le travail algébrique, on peut supposer que l'origine (0,0) est au point de lancement et de cette manière x_soit = Y_soit = 0.

Après avoir simplifié le paramètre "t«Il a été éliminé et l'équation qui demeure est et selon X: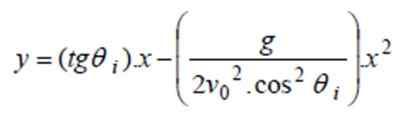

Ceci est l'équation de trajectoire en Forme explicite.

Trajectoire circulaire

Une trajectoire circulaire est donnée par:

(X - x_soit)² + (et et_soit)² = R²

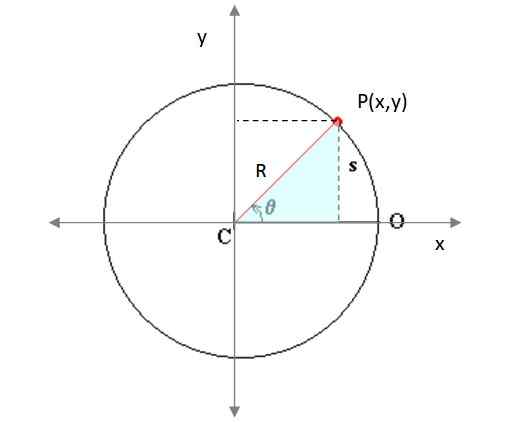Figure 4. Une particule se déplace dans une trajectoire circulaire sur le plan. Source: modifiée par f. Chaussure Wikimedia Commons.

Ici x_soit et et_soit Ils représentent le centre de la circonférence décrite par le mobile et R est le rayon du même. P (x, y) est un point de la trajectoire. Du triangle du rectangle ombré (figure 3), il est averti que:

x = r. cos θ

y = r. sin θ

Le paramètre, dans ce cas, est l'angle de balayage θ, appelé déplacement angulaire. Dans le cas particulier que la vitesse angulaire ω (angle balayé par unité de temps) est constant, on peut affirmer que:

θ = θ_soit + Ωt

Où θ_soit C'est la position angulaire initiale de la particule, qui est prise comme 0, est réduite à:

θ = Ωt

Dans ce cas, le temps revient aux équations paramétriques telles que:

x = r.cos ωt

y = r. péché Ωt

Les vecteurs unitaires Toi et J Ils sont très pratiques pour écrire la fonction de position d'un objet r (T). Ils indiquent les directions sur l'axe X Et sur l'axe et respectivement. En termes, la position d'une particule qui décrit un mouvement circulaire uniforme est:

r (t) = r.cos ωt Toi + R. péché Ωt J

Exercices résolus

Exercice résolu 1

Un canon peut tirer une balle à une vitesse de 200 m / s et un angle de 40º par rapport à l'horizontal. Si le lancement est effectué sur un terrain plat et que la résistance de l'air est méprisée, trouvez:

a) l'équation de trajectoire et (x) ..

b) les équations paramétriques x (t) et et T).

c) la portée horizontale et le temps où le projectile dure dans l'air.

d) La hauteur à laquelle le projectile est situé lorsque x = 12.000 m

Solution à)

a) Pour trouver la trajectoire, les valeurs données dans l'équation y (x) de la section précédente sont remplacées:

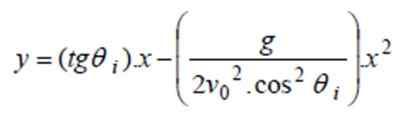
et (x) = tg 40º. X - 9.8 / (2 '400². cos²40º) X² ⇒  et (x) = 0.8391 x - 0.0000522X²

Solution b)

b) Le point de lancement est choisi à l'origine du système de coordonnées (0,0):

x (t) = x_soit +V_bœuf.T = 400'Cos 40º.T = 306.42. t.

et (t) = y_soit +V_Oy.T -½g.t²= 400 'Sen 40º.T - 0.5 '9.8T²= 257.12 T - 4.9.t²

Solution C)

c) Pour trouver le temps que le projectile dure dans les airs, cela est fait et (t) = 0, Être le lancement est fabriqué en terrain plat:

Peut vous servir: qu'est-ce que la rugosité relative et absolue?

0 = 257.12.T - 4.9.t²

T = 257.12/4.9 s = 52.473 s

La portée maximale horizontale remplace cette valeur x (t):

X_Max = 306.42'52.47 M = 16077.7 m

Une autre façon de trouver x_Max Il fait directement y = 0 dans l'équation de la trajectoire:

0 = 0.8391 x_Max - 0.0000522 x²_Max

x = 0.8391/0.0000522 M = 16078.5m

Il y a une petite différence en raison de l'arrondi des décimales.

D) Solution

d) Pour connaître la hauteur lorsque x = 12000 m Cette valeur est remplacée directement dans l'équation de trajectoire:

et (12000) = 0.8391'12000 - 0.0000522'12000² M = 2552.4 m

Exercice résolu 2

La fonction de position d'un objet est donnée par:

r (t) = 3T Toi + (4 -5T²) J m

Trouver:

a) L'équation de la trajectoire. Quelle courbe est?

b) la position initiale et la position lorsque t = 2 s.

c) le déplacement fait après t = 2 s.

Solution

a) La fonction de position a été donnée en termes de vecteurs unitaires Toi et J, qui déterminent respectivement l'adresse sur les axes X et et, donc:

x (t) = 3T

et T) = 4 -5T²

L'équation de trajectoire et (x) Il nettoie t de x (t) et remplacer dans et T):

T = x / 3

et (x) = 4 -5. (x / 3)² = 4 - 5x²/ 9 (parabole)

b) La position initiale est: r (2) = 4 J m ; La position dans T = 2 s est r (2) = 6 Toi -16 J m

c) déplacement Dr C'est la soustraction des deux vecteurs de position:

Δr = r (2) - r (2) = 6 Toi -16 J- 4 J = 6 Toi - vingt J m

Exercice résolu 3

La Terre a un rayon r = 6300 km et il est connu que la période de rotation de son mouvement autour de son axe est un jour. Trouver:

a) L'équation de la trajectoire d'un point à la surface de la Terre et sa fonction de position.

b) La vitesse et l'accélération dudit point.

Solution à)

a) La fonction de position pour tout point d'orbite circulaire est:

r (t) = r.cos ωt Toi + R.péché Ωt J

Vous avez le rayon de la Terre R, mais pas la vitesse angulaire ω, mais elle peut être calculée à partir de la période, sachant que pour le mouvement circulaire, il est valable de dire que:

Ω = 2π × Fréquence = 2π / période

La période de mouvement est: 1 jour = 24 heures = 1440 minutes = 86400 secondes, par conséquent:

Ω =  2π / 86400 s = 0.000023148 ​​S^-1

Remplacement dans la fonction de position:

r (t) = r.cos ωt Toi + R. péché Ωt J = 6300 (cos 0.000023148T Toi + péché 0.000023148T J) Km

Le chemin du chemin sous une forme paramétrique est:

x (t) = 6300. COS 0.000023148T

et (t) = 6300. péché 0.000023148T

Solution b)

b) Pour le mouvement circulaire, l'ampleur de la vitesse linéaire V d'un point est lié à la vitesse angulaire W à travers:

V = ΩR = 0.000023148 ​​S^-1'6300 km = 0.1458 km / s = 145.8 m / s

Même être un mouvement constant de 145.8 m / s, Il y a une accélération qui pointe vers le centre de l'orbite circulaire, responsable de la maintenance dans la rotation. C'est l'accélération centripète pour_c, donné par:

pour_c = V² / R = (145.8 m / s)² / 6300 × dix³ m = 0.00337 m / s².

Les références

1. Giancoli, D. La physique. (2006). Principes avec les applications. 6^e Prentice Hall. 22-25.
2. Kirkpatrick, L. 2007. Physique: un regard sur le monde. 6^faire Édition abrégée. Cengage Learning. 23 - 27.
3. Resnick, r. (1999). Physique. Volume 1. Troisième édition en espagnol. Mexique. Société de rédaction continentale S.POUR. de c.V. 21-22.
4. Rex, un. (2011). Fondamentaux de la physique. Pearson. 33 - 36
5. Sears, Zemansky. (2016). Physique universitaire avec physique moderne. 14^e. Élégant. Volume 1. 50 - 53.
6. SERAY, R., Jewett, J. (2008). Physique pour la science et l'ingénierie. Volume 1. 7^mame. Édition. Mexique. Cengage Learning Editors. 23-25.
7. SERAY, R., Vulle, c. (2011). Fondamentaux de la physique. 9^{n / A} Élégant. Cengage Learning. 43 - 55.
8. Wilson, J. (2011). Physique 10. Pearson Education. 133 - 149.