Propriétés de transformations linéaires, quels sont les types d'utilisation, les types, les exemples

Ongle Transformation linéaire, que nous appellerons simplement, relie les éléments de deux espaces vectoriels V et W, attribuant chaque vecteur V appartenant à V un seul vecteur W qui appartient à w, via une opération spécifique.

Cette transformation remplit deux conditions:

Figure 1. Une transformation linéaire s'applique à un vecteur d'espace vectoriel V pour obtenir un autre vecteur appartenant à l'espace vecteur w. Source: F. Zapata.

-Condition 1

Il se réfère à l'ajout, de sorte qu'une transformation en T doit être réalisée:

T (V + W) = T (V) + T (W)

-Condition 2

La deuxième condition représente l'homogénéité dans la multiplication d'un scalaire par un vecteur:

T (cV) = c⋅t (V)

La transformation linéaire, comme son nom l'indique, est responsable de la cartographie ou de la transformation des éléments de V en éléments de W.

La notation des fonctions est également utilisée dans le cas des transformations linéaires, donc le domaine de V est l'ensemble des éléments (vecteurs) à transformer, tandis que le codominium ou l'itinéraire est l'ensemble résultant.

Un exemple de transformation linéaire est:

Pour indiquer que la lettre t va être utilisée. La transformation sera appliquée à un vecteur V dont les composants sont X et Y, qui ont été représentés par une seule matrice de colonne. Le résultat est un autre vecteur W dont les composants sont x et 0, également représentés par une matrice de colonne.

Par conséquent, c'est une transformation de l'espace vectoriel r² Vers l'espace vectoriel r², qu'en résumé, il est écrit comme ceci:

T: R² → R²         

Si nous avons le vecteur:

La transformation nous renvoie:

Et donc avec n'importe quel vecteur r². Dans l'exemple 1, il sera vérifié que cette transformation est linéaire.

[TOC]

Propriétés des transformations linéaires

Supposons une transformation linéaire de v dans w, dans laquelle les vecteurs V et ou Ils appartiennent à V, puis les propriétés suivantes sont respectées:

Propriété 1

T (0) = 0

Où 0 est le vecteur nul.

Propriété 2

T (-V) = - t (V)

Propriété 3

T (ou  - V) = T (ou) - t (V)

Propriété 4

Être V = C₁V₁ + c₂V₂ +.. . +  c_nV_n

 Ensuite:

T (c₁V₁ + c₂V₂ +.. . +  c_nV_n) = c₁ T (V₁) + c₂ T (V₂) + .. . +  c_n T (V_n)

Éléments de transformation linéaire

Laissez V et W déjà mentionné des espaces vectoriels où la transformation linéaire T transforme les éléments de V en w. Nous pouvons définir les éléments suivants:

-Noyau C ou noyau: C'est un sous-ensemble du domaine auquel il est noté par NT) soit ker (t) et comprendre tous les éléments de V tels que:

T (V) = 0.

La transformation linéaire t (V) = 0 il s'appelle transformation nul.

Naturellement, le vecteur nul V = 0 remplit de toute façon avec cette condition, mais le noyau consiste en tout les vecteurs non nuls qui le remplissent également, pour un t donné.

Peut vous servir: fonction de croissance: comment l'identifier, des exemples, des exercices

-Image de t: C'est l'ensemble des vecteurs appartenant à w tels que l'image d'au moins un vecteur en V. Il est désigné comme Im t) Et c'est sous-ensemble de l'espace vectoriel w.

Ces éléments nous aideront à classer les transformations linéaires plus tard.

Que sont les transformations linéaires pour?

Initialement, les transformations linéaires fonctionnent avec des espaces vectoriels, formés par des vecteurs. Plusieurs fois, nous associons les vecteurs à la force et à d'autres amplitudes physiques, mais dans le traitement d'image numérique, un pixel peut être représenté par un vecteur.

Dans ce cas, l'image peut être manipulée par des transformations linéaires pratiques pour obtenir les effets souhaités, par exemple en projetant, en tournant, en trouvant l'image miroir ou en modifiant sa taille sans modifier les dimensions relatives.

Les transformations linéaires sont également largement utilisées en économie et en prise de décision, par exemple pour connaître la quantité de matières premières nécessaires pour fabriquer un certain lot de produit.

Le nombre de pièces nécessaires pour assembler les différents modèles produits par une usine, peut être travaillé par un arrangement de matrice, comme nous le verrons plus tard.

Types de transformations linéaires (classification)

Comme les fonctions, les transformations linéaires peuvent être:

-Injectif ou monomorphismes

-Bijectifs ou Épimorphismes

-Sur place ou Isomorphismes

En outre sont les types suivants:

-Endomorphismes

-Automorphes.

Transformations linéaires injectives

Laissez V et W Vector Spaces et T une transformation linéaire T: V → W. T est injectif lorsque:

Ker (T) = 0

Transformations de sur-place linéaire

Si V et W sont les espaces vectoriels tels que T: V → W, il est dit que T est bijectif lorsque:

Im (t) = w

Bijjective Linear Transformations

Une transformation linéaire t: v → w est bijective lorsqu'elle est à la fois injective et surcéd. Par conséquent, il est accompli que:

Ker (T) = 0 et Im (t) = w

Endomorphismes

Ce sont des transformations linéaires dans lesquelles le domaine et le coïncident.

Automorphes

Ce type de transformations linéaires sont des endomorphismes bijectifs.

Transformations linéaires spéciales

Opérateur linéaire

Une transformation linéaire t: v → v, qui va d'un espace vectoriel vers le même espace vectoriel est appelé Opérateur linéaire.

Transformation zéro

Mentionné ci-dessus, une transformation zéro est importante pour trouver le noyau d'une transformation linéaire:

Il peut vous servir: Tetradecágon

T: v → w tel que t (V) = 0 pour n'importe qui V.

Transformation d'identité

T: v → v tel que t (V) = V  pour n'importe qui V.

Transformation définie par une matrice

T: v → w tel que t (V) = AV, où a est une matrice et V C'est un vecteur de colonne.

Funtion linéaire

Les fonctions linéaires du type y = mx sont des transformations linéaires. Prenez par exemple y = 3x et voyez s'il remplit les deux conditions du début, en testant avec deux valeurs a et b n'importe quoi:

f (a + b) = 3 (a + b) = 3a + 3b = f (a) + f (b)

f (ka) = 3 (ka) = k⋅ (3a) = k⋅f (a)

En effet, c'est une transformation linéaire.

Applications

Les transformations linéaires ont des applications mathématiques, telles que:

-Rotation des essieux coordonnés.

-Dans la solution de systèmes d'équations différentielles linéaires.

-Problèmes d'auto-valeur et d'autovery.

Et ils ont également des applications dans d'autres domaines de la science, par exemple en mécanique, mécanique quantique et économie, entre autres domaines.

Exemples de transformations linéaires

Exemple 1

Dans de nombreux problèmes de mécanique, nous devons trouver la projection d'un vecteur V appartenant à l'espace, sur un certain plan. Ce vecteur V peut représenter par exemple une force.

Supposons que vous souhaitiez projeter le vecteur V = Sur le plan xy. Nous pouvons définir une transformation linéaire donnée par la matrice suivante:

Lorsque nous l'appliquons au vecteur V Nous obtenons un vecteur dont le composant Z est annulé. Géométriquement il est représenté, avec la projection de V Sur le plan XY comme le vecteur rouge avec deux composants.

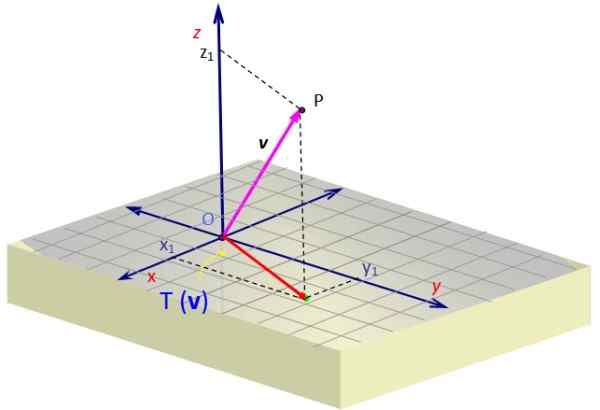Figure 2. Projection d'un vecteur dans l'espace sur un plan, qui est obtenu par une transformation linéaire. Source: F. Zapata.

Exemple 2

Supposons que vous ayez une usine qui produit trois types de chariots de jouets: C1, C2 et C3, pour lesquels vous avez à votre tour besoin de trois types de pièces en certaines quantités pour fabriquer chaque type de chariot:

-Haches ou pièce

-Roues ou pièce b

-Châssis ou pièce C

Pour chaque type de chariot, le nombre de pièces est différent, car les modèles sont différents. Nous pouvons accueillir les quantités dans une matrice 3 × 3, dans laquelle les colonnes sont dirigées par le type de chariot, et les rangs correspondent à la quantité de pièces nécessaires pour élaborer chaque modèle.

Ceci est un exemple de transformation donné par une matrice qui serait comme ceci:

Si l'usine reçoit un certain bon de commande, qui se compose de X quantité de C1, et  de C2 et z De C3, combien de pièces A, B et C doivent être disponibles pour assembler les chariots de commande?

Il peut vous servir: quelles sont les expressions algébriques et qui sont les plus fréquentes?

Nous devons trouver une transformation linéaire t (x) telle que:

Pour obtenir le vecteur et:

Qui nous donnera le nombre de pièces que nous devons avoir en disposition. Au cours de l'année résolue 2, nous évaluons l'efficacité des transformations linéaires pour trouver la quantité de pièces nécessaires pour répondre à un certain ordre.

Exercices résolus

- Exercice 1

Vérifiez que la transformation suivante T: R² → R² C'est linéaire:

Solution

Pour ce faire, vous devez vous assurer que la transformation remplit les deux conditions décrites au début, d'abord l'addition puis le produit d'un scalaire pour un vecteur. Vous devez donc prendre deux vecteurs V et  ou appartenant à r², les écrire par notation matricielle ou spécifier les composants.

Ces vecteurs sont:

V = x₁, et₁

ou = x₂, et₂

Première condition

-En rappelant que les vecteurs sont des composants ajoutés, il faut vérifier que:

T (V+ou) = T (V) + T (ou)

T (V+ou) = T (x₁+ X₂ ; et₁ + et₂)

De là, il est obtenu que:

T (x₁+ X₂ ; et₁ + et₂) = (x₁+ X₂; 0)

-D'un autre côté, lors de l'application de la transformation à chaque vecteur séparément:

T (x₁,et₁) + T (x₂,et₂) = (x₁,0) + (x₂,0)

En ajoutant les vecteurs résultants, il est effectivement obtenu:

W = (X₁+ X₂; 0)

Comme les deux résultats sont identiques, la première condition est satisfaite.

Deuxième condition

Maintenant, nous allons vérifier qu'en multipliant par un scler C, il peut sortir de la transformation:

T (cV) = c⋅t (V)

Sean:

V = x₁, et₁

c.V = C⋅X₁, C⋅y₁

Ensuite:

T (cV) = T (c⋅x₁, C⋅y₁ ) = (C⋅x₁ , 0)

Mais nous savons que de l'étape précédente que t (V) = T (x₁, et₁ ) = (X₁ , 0).

Ainsi, comme les deux expressions sont identiques, la deuxième condition est également remplie et la transformation est linéaire.

- Exercice 2

Une usine de chariot de jouet assemble trois modèles de véhicules: C1, C2 et C3, pour lesquels vous avez besoin de pièces A, B et C qui sont respectivement des essieux, des roues et du châssis. Les montants requis sont dans le tableau suivant:

L'usine a été invitée à préparer 12 modèles C1, 22 C2 et 16 C3. Combien de pièces A, B et C sont nécessaires pour terminer la commande?

Solution

Transformation linéaire t (x) = y est appliquée, dont le résultat est le produit entre les matrices:

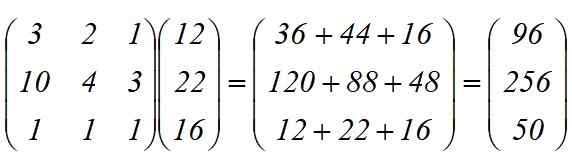
Ils sont requis au total:

-96 axes

-256 roues

-50 châssis.

Les références

1. Algèbre et géométrie analytique. Noyau et image. Classification des transformations linéaires. Récupéré de: Aga.FRA.UTN.Édu.ardente.
2. Grossman, s. 2012. Algèbre linéaire. 7e. Édition. McGraw Hill.
3. Guérrez, e. 2014. Algèbre linéaire et ses applications. Groupe éditorial de Patria.
4. Larson, R. 2016. Fondamentaux de l'algèbre linéaire. 6e. Édition. Cengage Learning.
5. Wikipédia. Applications linéaires. Récupéré de: est.Wikipédia.org.