Théorème de Varignon

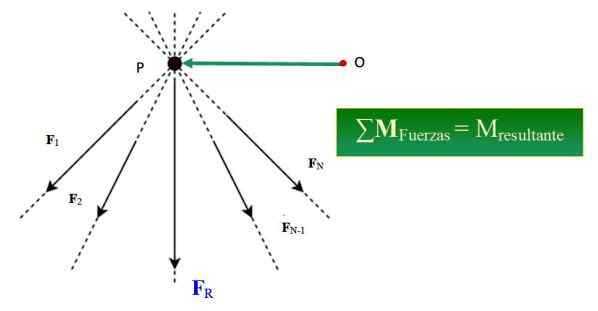
Figure 1.- Le théorème de Varignon affirme que la somme du moment des forces autour d'un certain point est équivalente au moment du résultat à ce sujet. Source: Wikimedia Commons / F. Zapata.

Qu'est-ce que le théorème de Varignon?

Le théorème de Varignon, en mécanique, indique que la somme des moments produits par un système de forces simultanées par rapport à un certain point, est égale au moment de la force résultante par rapport au même point.

Pour cette raison, ce théorème est également connu sous le nom Le début des moments.

Alors que le premier à dire que c'était le Néerlandais Simon Stevin (1548-1620), le créateur du paradoxe hydrostatique, le mathématicien français Pierre Varignon (1654-1722) était celui qui lui a par la suite donné sa forme définitive.

Un exemple de la façon dont le théorème de Varignon fonctionne en mécanique est le suivant: Supposons qu'un système simple de deux coplanares et de forces concurrentes agisse sur un point F₁ et F₂, (Indiqué avec audacieux pour son caractère vectoriel). Ces forces donnent naissance à une force nette ou qui en résulte, appelée F_R.

Chaque force exerce un couple ou un moment par rapport à un point ou, qui est calculé par le produit vectoriel entre le vecteur de position r_{Faire un coup de pouce} Et le strengh F, où r_{Faire un coup de pouce} Il est dirigé à partir ou au point de concurrence P:

M_O1 = r_{Faire un coup de pouce} × F₁

M_O2 = r_{Faire un coup de pouce} × F₂

Étant donné que F_R = F₁ + F₂, ensuite:

M_SOIT = r_{Faire un coup de pouce} × F₁ + r_{Faire un coup de pouce} × F₂ = M_O1 + M_O2

Mais comment r_{Faire un coup de pouce} Il s'agit donc d'un facteur commun en appliquant une propriété distributive au produit croisé:

M_SOIT = r_{Faire un coup de pouce} × (F₁ + F₂) = r_{Faire un coup de pouce} × F_R                

Par conséquent, la somme des moments ou des couples de chaque force par rapport au point ou équivaut à l'heure de la force résultante par rapport au même point.

Déclaration et démonstration

Être un système de n forces concurrentes, formées par F₁, F₂, F₃.. F_N, dont les lignes d'action sont destinées au point P (voir figure 1), le moment de ce système forces M_SOIT, Concernant un point ou est donné par:

Peut vous servir: équilibre instable: concept et exemples

M_SOIT = r_{Faire un coup de pouce} × F₁ + r_{Faire un coup de pouce} × F₂ + r_{Faire un coup de pouce} × F₃ +.. r_{Faire un coup de pouce} × F_N = r_{Faire un coup de pouce} × (F₁ + F₂ + F₃ +.. F_N)

Manifestation

Pour démontrer le théorème, la propriété distributive du produit vectoriel entre les vecteurs est fabriquée.

Être les forces F₁, F₂, F₃.. F_N appliqué à des points à₁, POUR₂, POUR₃… POUR_N et simultanément au point P. Le moment résultant de ce système, par rapport à un point ou, appelé M_SOIT, C'est la somme des moments de chaque force, en ce qui concerne ce point:

M_SOIT = ∑ r_Oai × F_Toi

Où va la somme de i = 1 à i = n, car il y a n forces. Comme ce sont des forces simultanées et puisque le produit vectoriel entre les vecteurs parallèles est nul, il arrive que:

r_Pai × F_Toi = 0

Avec le vecteur nul dénoté comme 0.

Le moment de l'une des forces concernant O, par exemple celle de la force F_Toi appliqué dans un_Toi, ça s'ecrit comme ça:

M_{J'ai entendu} = r_Oai × F_Toi

Le vecteur de position r_Oai  Il peut être exprimé comme la somme de deux vecteurs position:

r_Oai = r_{Faire un coup de pouce} + r_Pai

De cette façon, le moment concernant ou force F_Toi est:

M_{J'ai entendu} = (r_{Faire un coup de pouce} + r_Pai) × F_Toi = (r_{Faire un coup de pouce} × F_Toi) + (r_Pai × F_Toi)

Mais le dernier terme est nul, comme expliqué ci-dessus, car r_Pai est sur la ligne d'action de F_Toi, donc:

M_{J'ai entendu} = r_{Faire un coup de pouce} × F_Toi

Sachant que le moment du système par rapport au point ou est la somme de tous les moments individuels de chaque force par rapport à ce point, alors:

M_SOIT = ∑ M_{J'ai entendu} = ∑ r_{Faire un coup de pouce} × F_Toi

Comme r_{Faire un coup de pouce} Il est constant de la somme:

M_SOIT = r_{Faire un coup de pouce} × (∑ F_Toi)

Mais ∑ F_Toi C'est simplement le filet ou la force résultante F_R, Par conséquent, il est immédiatement conclu que:

Peut vous servir: Bouteille Leyden: pièces, opération, expériences

M_SOIT = r_{Faire un coup de pouce} × F_R

Exemple

Le théorème de Varignon facilite le calcul du moment de force F En ce qui concerne le point ou la structure indiquée sur la figure, si la force est décomposée en ses composants rectangulaires et que le moment de chacun d'eux est calculé:

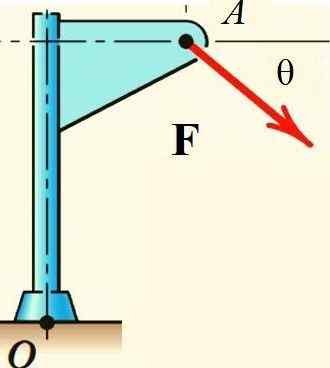Figure 2.- Le théorème de Varignon s'applique pour calculer le moment de force autour ou. Source: F. Zapata.

Applications du théorème de Varignon

Lorsque la force résultant d'un système est connue, le théorème de Varignon peut être appliqué pour remplacer la somme de chacun des moments produits par les forces qui la composent au moment de la résultante.

Si le système se compose de forces sur le même plan et le point par rapport auquel vous souhaitez calculer le moment appartient à ce plan, le moment résultant est perpendiculaire.

Par exemple, si toutes les forces sont dans le plan XY, le moment est dirigé sur l'axe z et ne reste que de trouver sa magnitude et sa signification, tel est le cas de l'exemple décrit ci-dessus.

Dans ce cas, le théorème de Varignon permet de calculer le moment résultant du système à travers la sommation. Il est très utile dans le cas d'un système de forces à trois dimensions, pour laquelle la direction du moment résultant n'est pas connue a priori.

Pour résoudre ces exercices, c'est pratique.

Exercice résolu

Par le théorème de Varignon, calculez le moment de force F autour du point ou illustré sur la figure si l'amplitude de F est de 725 N.

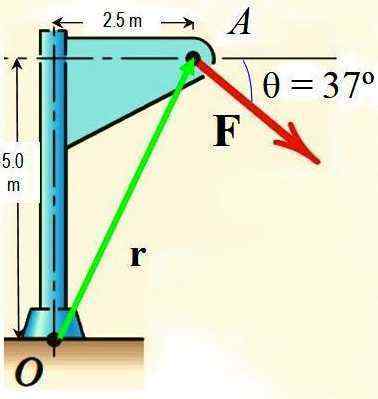figure 3.- Figure de l'exercice résolu. Source: F. Zapata.

Solution

Pour appliquer le théorème de Varignon, la force se décompose F en deux composants, dont les moments respectifs autour ou sont calculés et ajoutés pour obtenir le moment résultant.

Peut vous servir: corps rigide

F_X = 725 n ∙ cos 37 º = 579.0 n

F_et = - 725 N N ∙ Sen 37 º = −436.3 N

De même, le vecteur de position r Dirigé de ou vers A a les composants:

r_X = 2.5m

r_et = 5.0 m

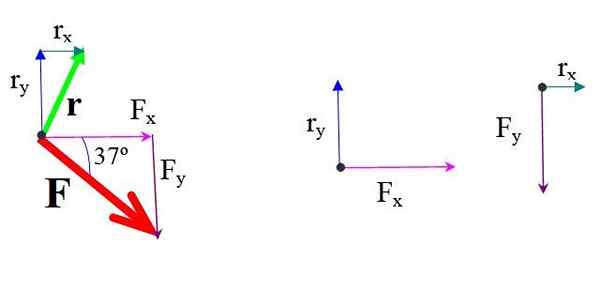Figure 4.- Composants de force et de position. Source: F. Zapata.

Le moment de chaque composant de la force par rapport à ou multipliez la force et la distance perpendiculaire.

Les deux forces ont tendance à faire pivoter la structure dans le même sens, ce qui dans ce cas est le sens du score, qui est arbitrairement attribué un signe positif:

M_Bœuf = F_X∙ R_et ∙ sin 90º = 579.0 n ∙ 5.0 m = 2895 n ∙ m

M_Oy = F_et∙ R_X ∙ sin (−90º) = −436.3 N ∙ 2.5 m ∙ (−1) = 1090.8 N ∙ M

Le moment résultant en ce qui concerne ou est:

M_SOIT = M_Bœuf + M_Oy = 3985.8 n ∙ m perpendiculaire à l'avion et dans un couple.

Les références

1. Bedford, 2000. POUR. Mécanique pour l'ingénierie: statique. Addison Wesley. 
2. Bière, f. 2010. Statique. McGraw Hill. 9na. Édition.
3. Hibbeler, R. 1992. Mécanique pour les ingénieurs. 6e. Édition. CECSA.
4. HK Engineering. Théorème de Varignon. Récupéré de: youtube.com.
5. Wikipédia. Théorème de Varignon (mécanique). Récupéré de: dans.Wikipédia.org.