Théorème de Chebyshov qui est, applications et exemples

Il Théorème de Chebyshov (ou l'inégalité de Chebyshov) est l'un des résultats classiques les plus importants de la théorie des probabilités. Il permet d'estimer la probabilité d'un événement décrit en termes de variable aléatoire x, en nous fournissant un niveau qui ne dépend pas de la distribution de la variable aléatoire mais de la variance de x.

Le théorème est appelé en l'honneur des mathématiques russes.

Cette inégalité, ou celles qui en raison de leurs caractéristiques, sont appelées l'inégalité de Chebyshov, est principalement utilisée pour approximer les probabilités au moyen de calculer les niveaux.

Quel est le théorème de Chebyshov?

Dans l'étude de la théorie des probabilités, il arrive que si la fonction de distribution d'une variable aléatoire x est connue, sa valeur attendue peut être calculée - ou l'espoir mathématique et (x) - et sa variance var (x), tant que celles-ci Les quantités existent. Cependant, réciproque n'est pas nécessairement vrai.

C'est-à-dire que la connaissance e (x) et var (x) ne peut pas nécessairement obtenir la fonction de distribution de x, donc des quantités telles que P (| x |> k) pour certains k> 0, sont très difficiles à obtenir. Mais grâce à l'inégalité de Chebyshov, il est possible d'estimer la probabilité de la variable aléatoire.

Le théorème de Chebyshov nous dit que si nous avons une variable aléatoire x sur un espace d'échantillonnage avec une fonction de probabilité P, et si k> 0, alors:

Peut vous servir: triangle acutangle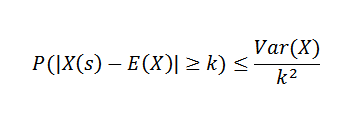

Applications et exemples

Parmi les nombreuses applications que possède le théorème de Chebyshov, ce qui suit peut être mentionné:

1. Limite de probabilité

C'est l'application la plus courante et est utilisée pour donner un niveau supérieur pour p (| x-e (x) | ≥k) où K> 0, uniquement avec la variance et l'espoir de la variable aléatoire x, sans connaître la fonction de probabilité.

Exemple 1

Supposons que le nombre de produits fabriqués dans une entreprise pendant une semaine soit une variable aléatoire avec une moyenne de 50.

S'il est connu que la variance d'une semaine de production est égale à 25, alors que pouvons-nous dire sur la probabilité que cette semaine, la production diffère de plus de 10 à la moyenne?

Solution

Appliquer l'inégalité de Chebyshov, nous devons:

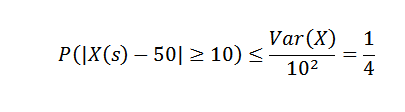
À partir de cela, nous pouvons obtenir que la probabilité que dans la semaine de production, le nombre d'articles dépasse en plus de 10 à la moyenne est au maximum 1/4.

2. Démonstration de théorèmes limites

L'inégalité de Chebyshov joue un rôle important dans la démonstration des théorèmes les plus importants. Par exemple, nous avons ce qui suit:

LOI LAIE LOI D'UN PROPRIÉ

Cette loi établit que compte tenu d'une succession x1, x2, ..., xn, ... de variables aléatoires indépendantes avec la même distribution moyenne e (xi) = μ et variance var (x) = σ², et un échantillon moyen connu de:

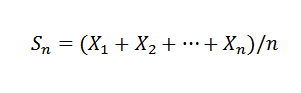
Donc pour k> 0 vous devez:

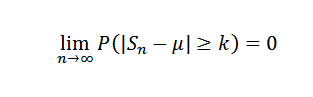
Ou équivalent:

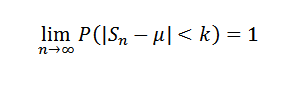
Manifestation

Nous remarquons d'abord ce qui suit:

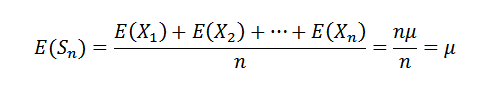
Comme x1, x2, ..., xn sont indépendants, il s'ensuit que:

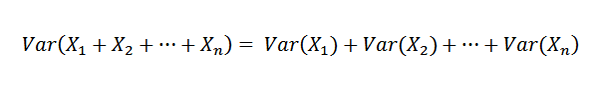
Par conséquent, il est possible d'affirmer ce qui suit:

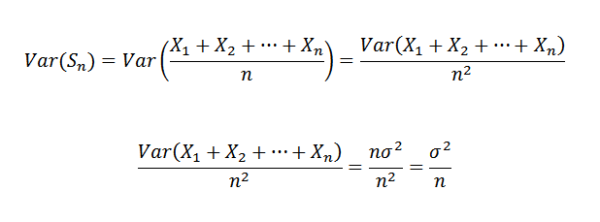
Ensuite, en utilisant le théorème de Chebyshov, vous devez:

Il peut vous servir: fonctions trigonométriques: basique, dans le plan cartésien, exemples, exercice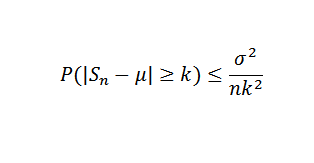

Enfin, le théorème résulte du fait que la limite de droite est nul lorsque n tend à l'infini.

Il convient de noter que ce test a été effectué uniquement pour le cas dans lequel il y a la variance de Xi; c'est-à-dire qu'il ne diverge pas. Ainsi, nous observons que le théorème est toujours vrai si e (xi) existe.

Théorème limite de Chebyshov

Si x1, x2, ..., xn, ... c'est une succession de variables aléatoires indépendantes telles qu'il y a du C0:

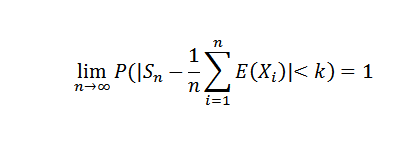
Manifestation

Comme la succession des variances est uniformément limitée, nous avons ce var (sn) ≤ c / n, pour tous les n naturels. Mais nous savons que:

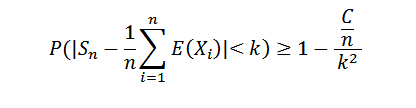
Faire n à l'infini, c'est ce qui suit:

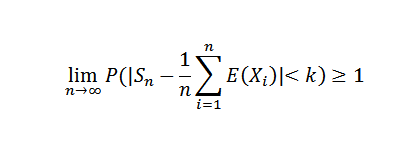
Comme une probabilité ne peut dépasser la valeur de 1, le résultat souhaité est obtenu. En conséquence de ce théorème, nous pourrions mentionner le cas particulier de Bernoulli.

Si un experimento se repite n veces de forma independiente con dos resultados posibles (fracaso y éxito), donde p es la probabilidad de éxito en cada experimento y X es la variable aleatoria que representa el número de éxitos obtenidos, entonces para cada k>0 il faut que:

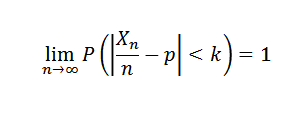
3. Taille de l'échantillon

En termes de variance, l'inégalité de Chebyshov nous permet de trouver une taille d'échantillon qui est suffisante pour garantir que la probabilité que | Sn-μ |> = K se produise est aussi petite que souhaité, ce qui vous permet d'avoir une approche de la moyenne.

Précisément, que ce soit x1, x2, ... xn un échantillon de variables aléatoires indépendantes de la taille n et supposons que e (xi) = μ et sa variance σ². Donc, en raison de l'inégalité de Chebyshov, vous devez:

Peut vous servir: numéro Euler ou numéro E: combien ok, propriétés, applications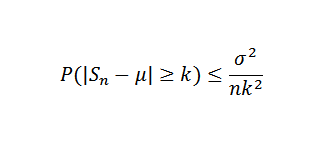

Maintenant être Δ> 0 fixe. Nous devons:

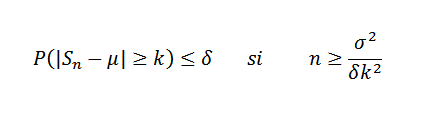
Exemple

Supposons que x1, x2, ... xn sont un échantillon de variables aléatoires indépendantes avec la distribution de Bernoulli, afin qu'ils prennent la valeur 1 avec probabilité p = 0.5.

Quelle devrait être la taille de l'échantillon pour garantir que la probabilité que la différence entre la moyenne arithmétique SN et sa valeur attendue (qui dépasse plus de 0,1) soit inférieure ou égale à 0.,01?

Solution

Nous devons (x) = μ = p = 0,5 et quel var (x) = σ²= P (1-p) = 0,25. Pour l'inégalité de Chebyshov, pour tout k> 0, nous devons:

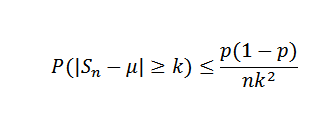
Maintenant, en prenant k = 0,1 et δ = 0,01, vous devez:

De cette façon, il est conclu qu'une taille d'échantillon d'au moins 2500 est nécessaire pour garantir que la probabilité de l'événement | Sn - 0,5 |> = 0,1 est inférieure à 0,01.

Inégalités de type Chebyshov

Il existe diverses inégalités liées aux inégalités de Chebyshov. L'une des plus connues est l'inégalité de Markov:

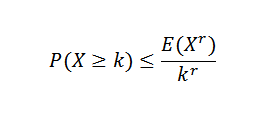
Dans cette expression x, c'est une variable aléatoire non négative avec k, r> 0.

L'inégalité de Markov peut prendre différentes formes. Par exemple, l'un ou l'autre et une variable aléatoire non négative (donc p (y> = 0) = 1) et supposons que e (y) = μ existe. Supposons également que (e (y))^r= μ_r Il y a pour un entier r> 1. Ensuite:

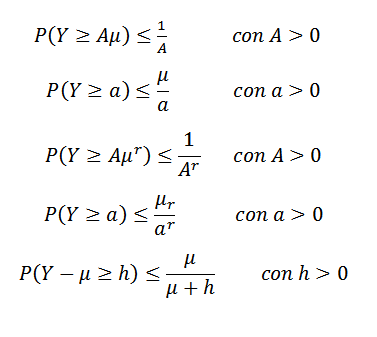
Une autre inégalité est celle de Gauss, qui nous dit que compte tenu d'une variable aléatoire x unimodale avec la mode à zéro, puis pour k> 0,