Propriétés de symétrie centrale, exemples et exercices

Deux points A et 'ont symétrie centrale En ce qui concerne un point ou lorsque le segment AA «le traverse et est également le milieu de AA». Au point ou s'appelle Centre de symétrie.

Le symétrique central d'un triangle ABC par rapport à un point ou, est un autre triangle a'b'c 'qui a les caractéristiques suivantes:

-Les segments homologues ont une durée égale 

-Leurs angles correspondants ont la même mesure.

Figure 1. ABC Triangle et son symétrique a'b'c '. Source: F. Zapata.

Dans la figure 1, un triangle ABC (rouge) et son a'b'c '(vert) symétrique central, par rapport au centre de symétrie ou. 

Dans cette même figure, un observateur attentif se rendrait compte que le même résultat est obtenu en appliquant une rotation du triangle d'origine, tant qu'elle est à 180 ° et axée sur ou.

Par conséquent, une symétrie centrale équivaut à un virage à 180 ° par rapport au centre de symétrie.

[TOC]

Propriétés de la symétrie centrale

Une symétrie centrale a les propriétés suivantes:

-Le centre de symétrie est le milieu du segment qui rejoint un point avec son symétrie.

-Un point symétrique d'un autre situé dans le centre de symétrie, coïncide avec le centre de symétrie.

-Le symétrique central d'un triangle est un triangle congruent (égal) à l'original.

-L'image par symétrie centrale d'une circonférence est une autre circonférence de rayon égal.

-Un cercle a une symétrie centrale par rapport à son propre centre.

Figure 2. Conception avec symétrie centrale. Source: Pixabay.

-L'ellipse a une symétrie centrale par rapport à son centre.

-Un segment a une symétrie centrale par rapport à son point médian.

-Le triangle équilatéral n'a pas de symétrie centrale par rapport à son centre, car son symétrie, bien que conforme au premier, donne un triangle équilatéral tourné.

Il peut vous servir: y = 3sen (4x) période de fonction

-Les carrés ont une symétrie centrale par rapport à leur centre.

-Un Pentagone manque de symétrie centrale par rapport à son centre.

-Les polygones réguliers ont une symétrie centrale lorsqu'ils ont un certain nombre de côtés de couple.

Exemples

Les critères de symétrie ont de nombreuses applications en science et ingénierie. La symétrie centrale est présente dans la nature, par exemple les cristaux de glace et les toiles d'araignée ont ce type de symétrie.

De plus, de nombreux problèmes sont facilement résolus lorsque l'existence d'une symétrie centrale et d'autres types de symétrie est utilisée. Par conséquent, il est pratique de s'identifier rapidement quand il se produit.

figure 3. Les cristaux de glace ont une symétrie centrale. Source: Pixabay.

Exemple 1

Étant donné un point P des coordonnées (a, b), vous devez trouver les coordonnées de son p 'symétrique concernant l'origine ou les coordonnées (0, 0).

La première chose est de construire le P 'P', pour lequel une ligne est tracée qui passe par l'origine ou par le point P. L'équation de cette ligne est y = (b / a) x.

Appelons maintenant (A ', B') les coordonnées du point symétrique P '. Point P. De plus, la distance OP doit être égale à Op ', qui écrit analytiquement comme ceci:

√ (un² + b²) = √ (a '² + B '² )

Ce qui suit est de remplacer b '= [(b / a).A '] dans l'expression précédente et carré des deux côtés de l'égalité pour éliminer la racine carrée: (a² + b²) = [a '² + (B²/pour²).pour'²]]

En extrayant un facteur commun et en simplifiant, il est atteint à «² = A². Cette équation a deux vraies solutions: a '= + a ou a' = -a. 

Pour obtenir B ', nous utilisons à nouveau b' = (b / a) a '. Si la solution positive de A est remplacée, il est atteint que b '= b. Et lorsque la solution négative est remplacée, alors b '= -b. 

Peut vous servir: quels sont les 7 éléments de la circonférence?

La solution positive donne pour p 'le même point p, donc il est exclu. La solution négative offre définitivement les coordonnées du point symétrique:

P ': (-a, -b)

Exemple 2

Il est nécessaire de démontrer qu'un segment AB et son central symétrique a'b 'ont la même longueur.

En commençant par les coordonnées du point A, qui sont (AX, AY) et celles du point B: (bx, BY), la longueur de l'AB est donnée par:

D (ab) = √ ((bx - ax)² + (Par - ay)² )

Par analogie, le segment symétrique a'b 'aura la longueur donnée par:

d (a'b ') = √ ((bx' - ax ')² + (Par '- ay')² )

Les coordonnées du point symétrique a 'sont ax' = -ax et ay '= -ay. De même, ceux de b 'sont bx' = -bx et par '= -By. Si ces coordonnées sont remplacées dans l'équation de la distance d (a'b '), vous avez:

D (a'b ') = √ ((-bx + ax)² + (-By + ay)²) qui équivaut à:

 √ ((bx - ax)² + (Par - ay)²) = D (ab)

Être démontré que les deux segments ont la même longueur.

Exercices résolus

- Exercice 1

Démontrer d'une manière analytique que le Central Symétrique ou un cercle de rayon R et Centre ou, est la même circonférence d'origine.

Solution

L'équation d'un rayon R et du cercle central (0,0) est:

X² + et² = R² (Équation de circonférence c)

Si à chaque point p de la circonférence et des coordonnées (x, y), sa coordonnée symétrique p ') est trouvée, l'équation de la circonférence symétrique est:

X '² + et'² = R² (Équation de circonférence symétrique C ')

Maintenant, nous nous référons au résultat de l'exemple 1, qui conclut que les coordonnées d'un point P ', symétrique à p et coordonnées (a, b), est (-a, -b). 

Mais dans cet exercice, le point P a des coordonnées (x, y), donc son p 'symétrique aura des coordonnées x' = -x e y '= -y. Le remplacement dans l'équation de circonférence symétrique est:

Peut vous servir: Rhomboid: caractéristiques, comment éliminer le périmètre et la zone

(-X)² + (-et)² = R²

Ce qui équivaut à: x²+ et² = R², concluant que le symétrique central d'un cercle par rapport à son centre est la circonférence elle-même.

- Exercice 2

Démontrer de manière géométrique que la symétrie centrale préserve les angles.

Solution

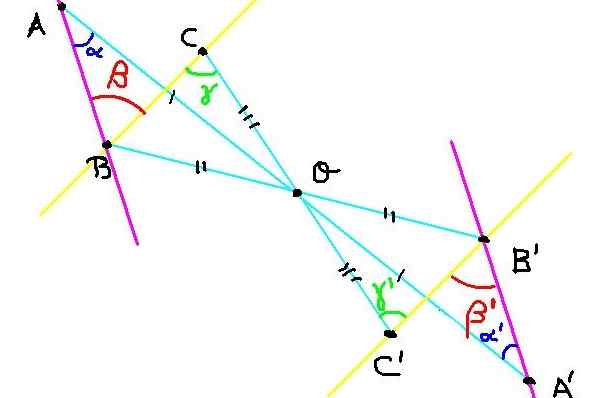Figure 4. Construction de points symétriques pour l'exercice 2. Source: F. Zapata.

Il y a trois points A, B et C dans l'avion. Son symétrique A ', B' et C 'est construit par rapport au centre de symétrie ou, comme le montre la figure 4. 

Maintenant, nous devons démontrer que l'angle ∡abc = β a la même mesure que l'angle ∡a'b'c '= β' '.

Comme C et C 'sont symétriques, alors OC = OC'. De même ob = ob 'y oa = oa'. D'un autre côté, l'angle ∡boc = ∡b'oc 'pour être opposé au sommet.

Ensuite, les triangles BOC et B'OC 'sont conformes pour avoir un angle égal entre les deux côtés égaux.

Parce que Boc est conforme à B'oc 'puis les angles  γ et γ ' Ils sont égaux. Mais ces angles, en plus de réaliser γ = γ ' Ce sont des lignes internes entre les lignes BC et B'C, ce qui implique que la ligne BC est parallèle à B'C '.

De même, Baa est conforme à B'oa 'de ce qui est suivi α = α ' . Mais  α et α ' Ce sont des angles alternatifs internes entre les lignes BA et B'A, dont il est conclu que la ligne BA est parallèle à b'a '.

Comme l'angle ∡abc = β a ses côtés parallèles avec l'angle ∡a'b'c '= β' et les deux sont aussi aigus, il est conclu que:

∡abc = ∡a'b'c '= β = β' '

Démontrant de cette manière que la symétrie centrale conserve la mesure des angles.

Les références

1. Baldor, J. POUR. 1973.Géométrie plate et espace. Culturel d'Amérique centrale. 
2. Lois et formules mathématiques. Systèmes de mesure d'angle. Récupéré de: Ingecanica.com.
3. Wentworth, G. Géométrie de la planète. Récupéré de: Gutenberg.org.
4. Wikipédia. Symétrie centrale. Récupéré de: est.Wikipédia.com
5. Wikipédia. Convoyeur. Récupéré de: est.Wikipédia.com
6. Zapata f. Angles conjugués internes et externes. Récupéré de:.com