Angles complémentaires qui et comment sont calculés, exemples, exercices

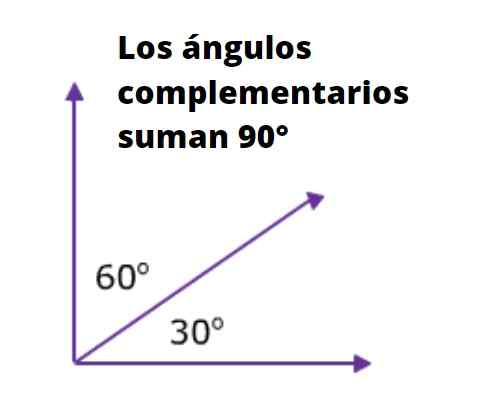
Deux angles ou plus sont angles complémentaires Si la somme de ses mesures correspond à celle d'un angle droit. Comme on le sait, la mesure d'un angle droit en degrés est de 90 °, et dans les rayons, il est π / 2.

Par exemple, les deux angles adjacents à l'hypoténuse d'un triangle rectangle sont complémentaires les uns des autres, car la somme de leurs mesures est de 90 °. La figure suivante est très illustrative à ce sujet:

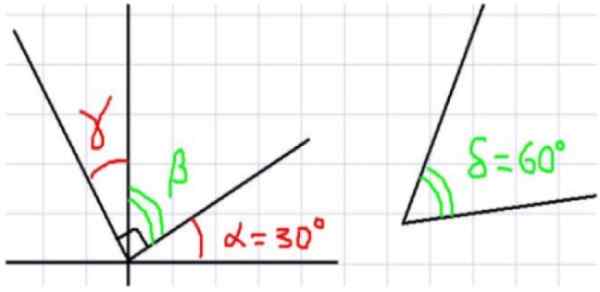Figure 1. À gauche, plusieurs angles avec un sommet commun. À droite un angle de 60º qui complète l'angle α (alpha). Source: F. Zapata.

La figure 1 montre un total de quatre angles. α et β sont complémentaires car ils sont adjacent Et sa somme complète un angle droit. De même, β est complémentaire de γ, où il s'ensuit que γ et α sont d'une même mesure.

Maintenant, comme la somme de α et δ est égale à 90 degrés, on peut dire que α et δ sont complémentaires. De plus, comme β et δ ont le même α complémentaire, on peut dire que β et δ ont la même mesure.

 [TOC]

Exemples d'angles complémentaires

Dans les exemples suivants, il est demandé de trouver les angles inconnus, indiqués par l'interrogatoire de la figure 2.

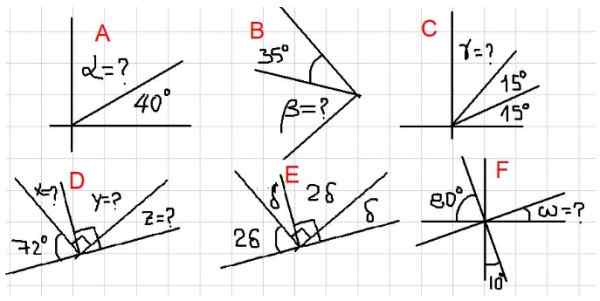Figure 2. Divers exemples d'angles complémentaires. Source: F. Zapata.

- Exemples A, B et C

Les exemples suivants sont dans l'ordre de la complexité.

Exemple A

Dans la figure supérieure, nous avons que les angles adjacents α et 40º s'additionnent à un angle droit. C'est α + 40º = 90º, donc α = 90º-- 40º = 50º.

Exemple B

Comme β est complémentaire avec l'angle de 35º, alors β = 90º - 35º = 55º.

Peut vous servir: Orthoedro: formules, zone, volume, diagonale, exemples

Exemple C

À partir de la figure 2c, la somme de γ + 15º + 15º = 90º. C'est-à-dire que γ est complémentaire à l'angle 30 = 15º + 15º. De manière que:

γ = 90º-- 30º = 60º

- Exemples D, E et F

Dans ces exemples, il y a plus d'angles impliqués. Pour trouver les inconnues, le lecteur doit appliquer le concept d'angle complémentaire autant de fois que nécessaire.

Exemple D

Comme x est complémentaire avec 72º, il s'ensuit que x = 90º - 72º = 18º. De plus et il est complémentaire avec x, alors y = 90º - 18º = 72º.

Enfin Z est complémentaire et. Depuis tout ce qui précède, il suit que:

Z = 90º - 72º = 18º

Exemple E

Les angles Δ et 2Δ sont complémentaires, donc Δ + 2Δ = 90º.

C'est 3Δ = 90º, ce qui implique que Δ = 90º / 3 = 30º.

Exemple F

Si nous appelons l'angle entre Ω et celui de 10, il a ensuite dû leur être complété, car il est observé que leur somme complète un angle droit. Où il suit que u = 80º. Comme u est complémentaire avec ω, alors ω = 10º.

Exercices

Trois exercices sont proposés ci-dessous. Dans chacun d'eux, la valeur des angles A et B doit être trouvée en degrés, de sorte que les relations illustrées à la figure 3 sont satisfaites.

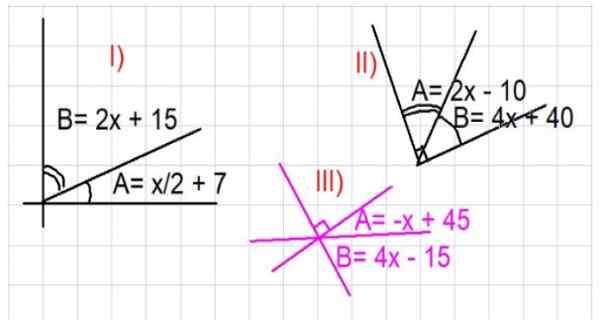figure 3. Illustrations pour exercices d'angles complémentaires. Source: F. Zapata.

- Exercice 1

Déterminez les valeurs des angles a et b de la partie I) de la figure 3.

Solution

D'après la figure montrée, on constate que A et B sont complémentaires, donc A + B = 90º. L'expression de A et B est remplacée en fonction de x donnée dans la partie I):

Peut vous servir: Radio de convergence: définition, exemples et exercices résolus

(x / 2 + 7) + (2x + 15) = 90

Ensuite, les termes sont correctement groupés et une simple équation linéaire est obtenue:

(5x / 2) + 22 = 90

La soustraction de 22 dans les deux membres est:

5x / 2 = 90 -22 = 68

Et enfin la valeur de x est effacée:

x = 2 * 68/5 = 136/5

Maintenant, l'angle se trouve en remplacement de la valeur de x:

A = (136/5) / 2 +7 = 103/5 = 20,6 º.

Tandis que l'angle B est:

B = 2 * 136/5 + 15 = 347 / 5º = 69,4º .

- Exercice 2

Trouvez les valeurs des angles A et B de l'image II, figure 3.

Solution

Encore une fois, comme a et b sont des angles complémentaires, vous devez: a + b = 90º. Le remplacement de l'expression de A et B en fonction de x donnée dans la partie II) de la figure 3 est:

(2x - 10) + (4x +40) = 90

Les termes similaires sont regroupés pour obtenir l'équation:

6 x + 30 = 90

La division des deux membres entre 6 est obtenue:

x + 5 = 15

Où il suit que x = 10º.

Donc:

A = 2 * 10 - 10 = 10º

B = 4 * 10 + 40 = 80º.

- Exercice 3

Déterminer les valeurs des angles A et B de la partie III) de la figure 3.

Solution

La figure est soigneusement analysée pour rechercher des angles complémentaires. Dans ce cas, vous devez + b = 90 degrés. Remplacement de l'expression de A et B en fonction de X donnée sur la figure, vous avez:

(-X +45) + (4x -15) = 90

3 x + 30 = 90

Diviser les deux membres par 3 est la suivante:

x + 10 = 30

Où il suit que x = 20º.

C'est-à-dire que l'angle a = -20 +45 = 25º. Et pour sa part: b = 4 * 20 -15 = 65º.

Angles des côtés perpendiculaires

On dit que deux angles sont côtés perpendiculaires Si chaque côté a son perpendiculaire correspondant dans l'autre. La figure suivante clarifie le concept:

Peut vous servir: succession composée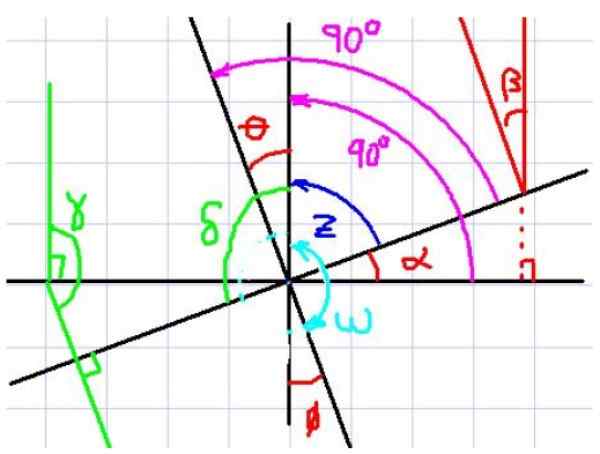Figure 4. Angles des côtés perpendiculaires. Source: F. Zapata.

Dans la figure 4, les angles α et θ sont observés, par exemple. Remarquez maintenant que chaque angle a sa perpendiculaire correspondante à l'autre angle.

On voit également que α et θ ont le même angle complémentaire z, Par conséquent, l'observateur conclut immédiatement que α et θ ont la même mesure. Il semble alors que si deux angles ont des côtés perpendiculaires l'un avec l'autre, ils sont les mêmes, mais voyons un autre cas.

Considérez maintenant les angles α et ω. Ces deux angles ont également des côtés perpendiculaires correspondants, mais on ne peut pas dire qu'ils sont de même mesure, car l'un est aigu et l'autre est obtus.

Notez que ω + θ = 180º. Outre θ = α. Si vous remplacez cette expression de Z dans la première équation, vous obtenez:

Δ + α = 180º, étant que Δ et α sont des angles de côtés mutuellement perpendiculaires.

Règle générale pour les angles des côtés perpendiculaires 

De la susmention, une règle qui est toujours respectée que les angles ont des côtés perpendiculaires peuvent être établis:

Si deux angles sont mutuellement perpendiculaires, alors ils sont les mêmes si les deux sont aigus ou les deux sont obtus. Sinon, si l'un est aigu et l'autre est obtus, alors ils sont supplémentaires, c'est-à-dire qu'ils ajoutent 180º.

Appliquer cette règle et en référence aux angles de la figure 4, nous pouvons affirmer ce qui suit:

α = β = θ = φ

γ = Δ

Avec l'angle supplémentaire ω de α, β, θ et φ.

Les références

1. Baldor, J. POUR. 1973. Géométrie plate et espace. Culturel d'Amérique centrale. 
2. Lois et formules mathématiques. Systèmes de mesure d'angle. Récupéré de: Ingecanica.com.
3. Wentworth, G. Géométrie de la planète. Récupéré de: Gutenberg.org.
4. Wikipédia. Angles complémentaires. Récupéré de: est.Wikipédia.com
5. Wikipédia. Convoyeur. Récupéré de: est.Wikipédia.com
6. Zapata f. Goniomètre: historique, pièces, opération. Récupéré de:.com