Symétrie

Qu'est-ce que la symétrie?

La symétrie C'est lorsque les parties d'une figure correspondent exactement à la taille, à la forme et à la position. Si vous divisez une image, un objet ou d'être vivant avec une ligne imaginaire et que les deux côtés sont les mêmes, vous pouvez dire qu'il est symétrique. 

Cette ligne imaginaire est appelée axe de symétrie et, dans la même figure, il peut y avoir des axes symétriques différents qui le divisent, générant des parties égales qui coïncidront exactement si les superpones.

Cœur symétrique, avec axe de symétrie

Un moyen très simple de corroborer si une figure que nous avons sur une feuille de papier est symétrique, est de tracer une ligne droite dans la moitié du dessin, puis de plier la figure. Si les deux parties sont d'accord, ce chiffre est symétrique par rapport à la ligne que vous tracez, et s'ils ne coïncident pas, il peut ne pas avoir de symétrie ou que vous devez tracer la ligne droite d'une autre manière.

Asymétrie et symétrie

Lorsque nous disons qu'une figure est asymétrique, nous voulons dire qu'elle ne peut pas être divisée par moitié par une ligne, pour obtenir deux parties égales. Par exemple, l'arbre suivant est asymétrique:

Arbre asymétrique

Si vous examinez votre propre corps, vous pouvez également trouver des exemples de symétrie. Observez soigneusement vos mains, les deux ont une symétrie partielle, car ils ont beaucoup l'air, ils ont une taille similaire, ils ont cinq doigts et un clou à chaque doigt. 

La symétrie dans ce cas n'est pas complète car les empreintes digitales sont différentes entre une main et une autre, et parce que chaque main peut compter sur de petites caractéristiques qui le différencient de l'autre, comme les blessures, les cicatrices ou les mords, comme le lunaire. 

Symétrie dans l'antiquité

Dans les temps anciens, les Grecs considéraient que les plus belles personnes étaient celles qui avaient un visage symétrique, et on pensait que la symétrie était une caractéristique qui démontrait la perfection. 

Peut vous servir: programmation linéaire: à quoi sert, modèles, restrictions, applications

Cette idée de symétrie comme quelque chose de parfait a été présent à différents moments de l'humanité. En fait, l'une des œuvres les plus célèbres de l'histoire est L'homme vitruvien, Préparé par l'artiste italien de la Renaissance Leonardo da Vinci.

L'homme vitruvien

Ce dessin est utilisé avec précision pour montrer quelle symétrie est, dans ce cas, appliqué au corps humain. 

Où pouvons-nous trouver plus symétrie?

Nous pouvons trouver la symétrie dans les dessins, en biologie, où les organismes végétaux et animaux peuvent présenter des propriétés symétriques.

Aussi en géométrie, dans les objets du quotidien, et peut également être présent dans la musique et la littérature, car il existe des compositions musicales symétriques, ainsi que des textes et des poèmes qui ont cette propriété. 

Une procédure courante lors de la création de pièces musicales est de placer des séquences avec la répétition des sons encore et encore. Il arrive également qu'une phrase musicale ait des raisons qui sont répétées de manière identique ou qui sont répétées plus aiguës ou plus sérieuses. 

Dans le cas de la littérature, il est possible de construire des phrases afin qu'ils lisent également de gauche à droite, comme: 

Je dis des roses, je ne donne pas, Que, si vous l'investissez, dit exactement le même. 

Dans la poésie, la symétrie est également largement utilisée par rapport aux versets qui composent un poème. 

Exemples de symétrie

Les chiffres symétriques peuvent être très simples ou très complexes. Et vous pouvez trouver des images avec symétrie à la fois en géométrie et en art, ainsi que dans la vraie vie. 

- Le papillon inférieur a un axe de symétrie et est symétrique. Mais il y a d'autres cas où les images ont deux ou plusieurs axes symétriques.

Peut vous servir: Coordonnées cylindriques: système, changement et exercices

- Si vous observez ce chiffre, vous remarquerez qu'il a deux axes de symétrie, un vertical et un horizontal: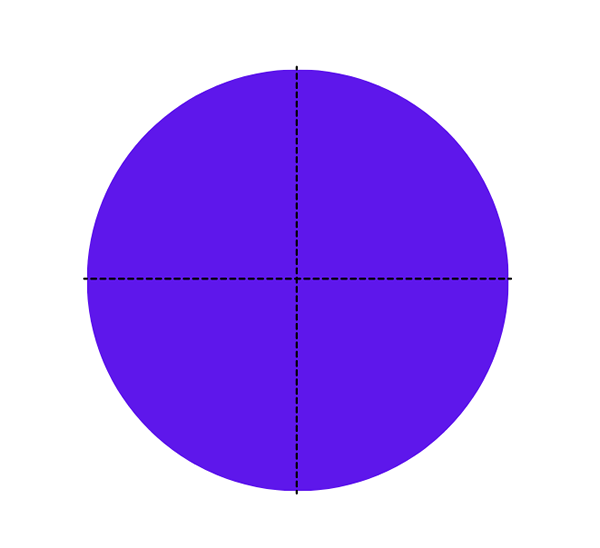

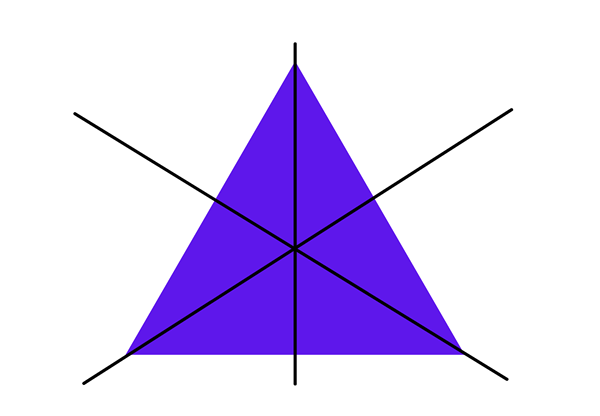
- Ce triangle est une figure géométrique avec trois axes de symétrie. Lors du dessin de ces trois lignes, le résultat sera que la figure sera divisée en deux parties identiques.

- Dans cette étoile, vous pouvez trouver quatre axes de symétrie:

- Symétrie bilatérale chez les animaux. C'est un type de symétrie qui implique la division d'un organisme dans la moitié droite et gauche, séparée par un axe.

- Il existe également d'autres exemples dans la nature qui présentent un type de symétrie différent qui est connu sous le nom de symétrie radiale, et qui est caractérisé parce que vous pouvez transformer l'organisme et son image reste la même. Les étoiles de la mer sont des organismes qui ont une symétrie radiale. 

- Lorsque nous parlons de symétrie d'expansion, nous nous référons à celle dans laquelle les parties ont la même forme, mais elles grandissent en taille, comme avec la série de poupées russes appelées matriosques.

- Les autres types de symétrie sont la symétrie du découragement, qui est réalisée dans deux parties égales d'un objet lorsqu'un virage à 180 degrés est réalisé.

- La symétrie de la traduction fait référence à un ensemble de répétitions qui effectuent un objet à une distance toujours identique de l'axe, qui génère que la forme est répétée le long d'une ligne constante, comme cela se produit avec les colonnes d'un temple grec. 

Exercices de symétrie: dessins

Vous pouvez également faire vos propres dessins symétriques à la maison, avec l'aide de dessins comme ceux-ci. Vous devez dessiner le soleil et le parapluie de sorte que la partie qui est à droite de l'axe de symétrie soit égale à la gauche.

Peut vous servir: grade d'un polynôme: comment il est déterminé, exemples et exercices

Soleil

Parapluie

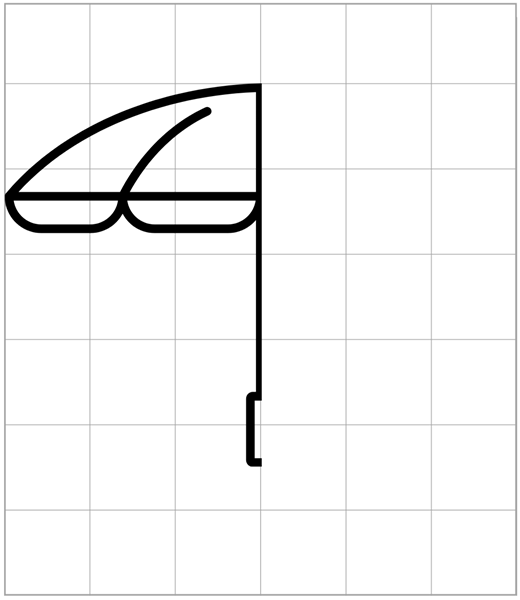
Une autre façon de faire une figure symétrique sur le papier est de plier une feuille avec une grille en deux et avec un tirage à la baisse épais sur moitié plié moitié. L'idée est que le marqueur transporte le papier, et donc, lorsque vous le dépliez, vous aurez créé une figure symétrique par rapport à la ligne qui forme le pli dans la feuille.