Série d'exemples de puissance et d'exercices

Ongle Séries de puissance Il se compose d'une somme de termes sous forme de pouvoirs de la variable X, ou plus généralement, de X-C, où c C'est un nombre réel constant. Dans la sommation de la somme, une série de pouvoirs est exprimée comme suit:

∑A_n (X -c)ⁿ = A_soit + pour₁ (x - c) + a₂ (X - c)² + pour₃ (X - c)³ +… + A_n (X - c)ⁿ

Où les coefficients_soit, pour₁, pour₂… Ce sont des nombres réels et la série commence à n = 0.

Figure 1. Définition d'une série de puissance. Source: F. Zapata.

Cette série est axée sur la valeur c c'est constant, mais vous pouvez choisir cela c Être égal à 0, auquel cas les pouvoirs sont simplifiés:

∑A_n Xⁿ = A_soit + pour₁ x + a₂ X² + pour₃ X³ +… + A_n Xⁿ

La série commence par pour_soit(X-C)⁰ et pour_soitX⁰ respectivement. Mais nous savons que:

(X-C)⁰= x⁰ = 1

Donc pour_soit(X-C)⁰ = pour_soitX⁰ = pour_soit (Terme indépendant)

La bonne chose à propos des pouvoirs des pouvoirs est qu'avec eux, vous pouvez exprimer des fonctions et cela présente de nombreux avantages, surtout si vous voulez travailler avec une fonction compliquée.

Lorsque c'est le cas, au lieu d'utiliser directement la fonction, son développement de puissance est utilisé, ce qui peut être plus facile à dériver, à intégrer ou à travailler numériquement.

Bien sûr, tout est conditionné à la convergence de la série. Une série converge lorsque en ajoutant une certaine quantité de termes, une valeur fixe est obtenue. Et si nous ajoutons plus de termes, nous continuons à obtenir cette valeur.

[TOC]

Fonctionne comme des pouvoirs de pouvoirs

Comme exemple d'une fonction exprimée comme une série de puissance, prenons f (x) = e^X.

Cette fonction peut être exprimée en termes de série de pouvoirs comme suit:

et^X  ≈ 1 + x + (x² / 2!) + (X³ / 3!) + (x⁴ / 4!) + (x⁵ / 5!) + ..

Où! = n. (N-1). (N-2). (N-3)… et il est pris 0! = 1.

Nous allons vérifier à l'aide d'une calculatrice, que la série coïncide efficacement avec la fonction explicitement donnée. Par exemple, commençons à faire x = 0.

Peut vous servir: probabilité théorique: comment le sortir, exemples, exercices

Nous savons que e⁰ = 1. Voyons ce que fait la série:

et⁰ ≈ 1 + 0 + (0² / 2!) + (0³ / 3!) + (0⁴ / 4!) + (0⁵ / 5!) +… = 1

Et maintenant essayons avec x = 1. Une calculatrice jette que et¹ = 2.71828, Et puis comparons la série:

et¹ ≈ 1 + 1 + (1² / 2!) + (1³ / 3!) + (1⁴ / 4!) + (1⁵ / 5!) +… = 2 + 0.5000 + 0.1667 + 0.0417 + 0.0083 +… ≈ 2.7167

Avec seulement 5 mandats, nous avons déjà une coïncidence exacte dans e ≈ 2.71. Notre série manque un peu plus, mais à mesure que plus de termes sont ajoutés, avec toute certitude, la série converge vers la valeur exacte de et. La représentation est exacte lorsque N → ∞.

Si l'analyse précédente est répétée pour n = 2 Des résultats très similaires sont obtenus.

De cette façon, nous sommes sûrs que la fonction exponentielle f (x) = e^X Il peut être représenté par cette série de pouvoirs:

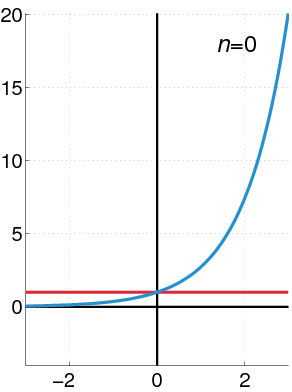Figure 2. Dans cette animation, il est considéré comme les pouvoirs sont plus proches de la fonction exponentielle car plus de termes sont pris. Source: Wikimedia Commons.

Pouvoirs géométriques des pouvoirs

La fonction f (x) = e^X Ce n'est pas la seule fonction qui admet une représentation en série des pouvoirs. Par exemple, la fonction  F(x) = 1/1 - x  Ça ressemble beaucoup au connu Série géométrique convergente:

∑A.rⁿ = A / 1 - r

Faites simplement a = 1 et r = x pour obtenir une série appropriée à cette fonction, qui est centrée sur c = 0:

Cependant, il est connu que cette série est convergente pour │r│<1, por lo tanto la representación es válida únicamente en el intervalo (-1,1), aunque la función sea válida para todo x, excepto x=1.

Lorsque vous souhaitez définir cette fonction dans un autre intervalle, elle se concentre simplement sur une valeur adéquate et prêt.

Comment trouver le développement de la série des pouvoirs d'une fonction

Toute fonction peut être développée dans une série de pouvoirs axés sur C, tant que vous avez dérivé de toutes les commandes à x = C. La procédure utilise le théorème suivant, appelé Théorème de Taylor:

Soit f (x) une fonction avec les dérivés d'ordre n, indiqué F^(N), qui admet un développement en série de pouvoirs dans l'intervalle Toi. Son développement dans Série Taylor est:

Il peut vous servir: quel est l'emplacement des nombres entiers et décimaux?

De manière que:

f (x) = f (c) + f '(c) (x-c) + f "(c) (x-c)² / 2 + f "(c) (x-c)³ / 6 +… r_n

Où r_n, qui est le nième de la série, il s'appelle résidu:

Lorsque c = 0, la série est appelée Série Maclaurin.

Cette série donnée ici est identique à la série donnée au début, mais maintenant il existe un moyen de trouver explicitement les coefficients de chaque terme, donné par:

Cependant, il faut s'assurer que la série transmet la fonction que vous souhaitez représenter. Il arrive que toutes les séries Taylor ne convergent pas nécessairement vers le f (x) qui était à l'esprit lors du calcul des coefficients pour_n.

Cela se produit parce que peut-être ceux dérivés de la fonction, évalué dans x = c coïncider avec la même valeur de ceux dérivés d'un autre, également en x = c. Dans ce cas, les coefficients seraient les mêmes, mais le développement serait ambigu en n'ayant pas la certitude dont la fonction correspond.

Heureusement, il existe un moyen de savoir:

Critères de convergence

Pour éviter l'ambiguïté, si R_n → 0 Lorsque n → ∞ pour tous les x dans l'intervalle I, la série converge vers f (x).

Exercer

- Exercice résolu 1

Trouvez les pouvoirs géométriques pour la fonction f (x) = 1/2 - x concentré sur c = 0.

Solution

La fonction donnée doit être exprimée d'une manière qui correspond autant que possible avec 1 / 1- x, dont la série est connue. Par conséquent, nous réécrivons le numérateur et le dénominateur, sans modifier l'expression originale:

1/2 - x = (1/2) / [1 - (x / 2)]

Comme ½ est constant, il sort de la somme, et cela est écrit en termes de nouvelle variable x / 2:

Peut vous servir: Binôme conjugué: comment il est résolu, exemples, exercices

Notez que x = 2 n'appartient pas au domaine de la fonction, et selon les critères de convergence donnés dans la section Série géométrique de puissance, Le développement est valable pour │x / 2│< 1 o equivalentemente -2 < x < 2.

- Exercice résolu 2

Trouvez les 5 premiers termes du développement de la série Maclaurin de la fonction f (x) = sen x.

Solution

Étape 1

Les dérivés sont d'abord:

-Dérivé de l'ordre 0: c'est la même fonction f (x) = sen x

-Première dérivée: (sin x) '= cos x

-Deuxième dérivé: (sin x) "= (cos x) '= - sin x

-Troisième dérivé: (sin x) "= (-sen x) '= - cos x

-Quatrième dérivé: (sin x) "= (- cos x) '= sin x

Étape 2

Ensuite, chaque dérivé est évalué à x = c, tout comme un développement de maclaurin, c = 0:

sin 0 = 0; cos 0 = 1; - sen 0 = 0; -Cos 0 = -1; sin 0 = 0

Étape 3

Les coefficients sont construits pour_n;

pour_soit = 0/0! = 0; pour₁ = 1/1! = 1; pour₂ = 0/2! = 0; pour₃ = -1 / 3!; pour₄ = 0/4! = 0

Étape 4

Enfin, la série est assemblée selon:

sin x ≈ 0.X⁰ + 1. X¹ + 0 .X² - (1/3!) X³ + 0.X⁴... = x - (1/3!)) X³  +..

Le lecteur a-t-il besoin de plus de termes? Combien de plus, la série est plus proche de la fonction.

Notez qu'il existe un modèle dans les coefficients, le terme non nul suivant est de₅ Et tout l'index impair est également différent de 0, alternant les signes, de sorte que:

Sen x ≈ x - (1/3!)) X³  + (1/5!)) X⁵ - (1/7!)) X⁷  +.. .

Il est laissé comme de l'exercice à vérifier, vous pouvez utiliser le rapport du quotient Pour la convergence en série.

Les références

1. Fondation CK-12. Série de puissance: représentation des fonctions et des opérations. Récupéré de: CK12.org.
2. Engler, un. 2019. Calcul intégral. Université nationale de la côte.
3. Larson, R. 2010. Calcul d'une variable. 9na. Édition. McGraw Hill.
4. Textes mathématiques gratuites. Séries de puissance. Récupéré de: mathématiques.Liibretexts.org.
5. Wikipédia. Séries de puissance. Récupéré de: est.Wikipédia.org.