Propriétés de la série Fibonacci, relations naturelles, applications

La Série O La succession de Fibonacci est une séquence de nombres obtenus en commençant par 0 et 1, continue avec la somme: 0 + 1 = 1, puis la somme des deux précédents: 1 + 1 = 2 et ainsi.

Suivant cette procédure, les autres termes sont obtenus, voyons: 2 + 1 = 3, 3 + 2 = 5, 5 + 3 = 8, 8 +5 = 13…

Premier nombre de la série Fibonacci

La procédure est répétée autant de fois que vous le souhaitez. De cette façon, la succession de Fibonacci acquiert la forme: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 .. Les nombres qui le font sont appelés Nombres de Fibonacci.

[TOC]

Histoire

La succession de Fibonacci s'appelle un mathématicien italien qui vivait au Moyen Âge: Leonardo de Pisa, également connu sous le nom de Fibonacci (1175-1250). 

Leonardo de Pisa

Leonardo a passé l'enfance en Afrique du Nord et a voyagé dans toute la Méditerranée, où il connaissait le système de numérotation indo-arabique et était ravi de lui. Les enseignants arabes de Leonardo lui ont probablement enseigné la succession, qui était déjà connue par les mathématiciens hindous.

Par la suite, lors du retour à Pisa Fibonacci a écrit un livre intitulé Liber Abaci (Le livre d'Abacus), où en plus de mettre en évidence les avantages des nombres indo-arabiques face à la numérotation romaine et à l'introduction de 0, il a soulevé un problème sur la reproduction des lapins.

Et la solution à ce problème est précisément le nombre de la succession de Fibonacci.

Leonardo de Pisa n'a pas reçu la création de la succession; Il ne l'a mentionné que dans son livre comme une curiosité, qui a attiré l'attention de nombreux chercheurs qui l'ont suivi. Parmi ceux-ci, le mathématicien français du XIXe siècle Edouard Lucas, qui, lors de l'étude de la succession, l'a baptisée avec le nom du sage médiéval qui l'a fait connaître en Occident.

Le problème des lapins Fibonacci

Le problème dit: il y a quelques lapins qui vivent pour toujours, ce qui, à deux mois, est fertile. Une fois la maturité réalisée, ils ont quelques bébés de sexe différents chaque mois, qui mettent également deux mois à reproduire et ont un couple mensuel de lapins.

Peut vous servir: lois de Morgan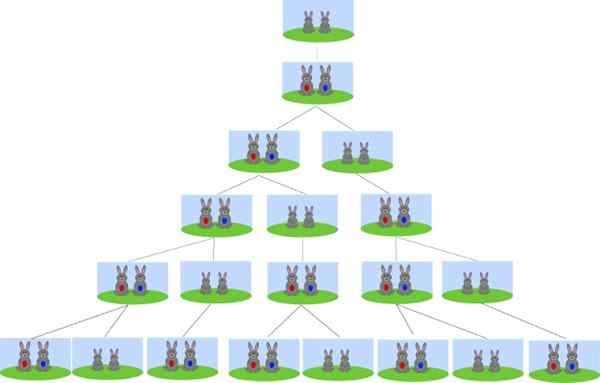L'origine de la succession de Fibonacci est dans le problème de la reproduction des lapins. Source: Wikimedia Commons.

En commençant par quelques lapins nouveau-nés, combien de paires de lapins seront dans un mois? Combien de paires de lapins seront après 2, 3 et 4 mois? Et combien seront après 6 mois?

La réponse est en nombres Fibonacci. Après 1 mois, il y a 1 paire de lapins, le couple d'origine, car ils ne se reproduisent qu'après 2 mois.

Après 2 mois, il y a 2 couples de lapins: le couple d'origine et leur première litière.

À 3 mois, nous aurons 3 couples, dont le couple d'origine, leur première litière et un nouveau.

Après avoir atteint le 4ème mois, nous aurons le couple d'origine, la première portée qui à son tour a leurs premiers enfants, la portée du troisième mois et une nouvelle litière. Au total, 5 paires de lapins.

Mais ce sont le nombre de la séquence Fibonacci, donc après 6 mois, il y aura 13 couples de lapins, car chaque mois, les couples des deux mois précédents sont ajoutés.

Propriétés de la série Fibonacci

Voici quelques propriétés intéressantes de la succession de Fibonacci.

Propriété 1

La formule récursive pour trouver les termes de la succession est:

pour_{N + 1} = A_n + pour_N-1  Pour n supérieur ou égal à 2.

Où n = 2, 3, 4, c'est-à-dire pour trouver le septième terme A₇, Nous faisons n = 6, de sorte que 6 + 1 = 7. Nous devons connaître les termes pour₅  déjà₆, de la liste qui apparaît dans l'introduction de₅ = 5 et un₆ = 8, donc à₇ = 5 + 8 = 13.

Propriété 2

Si les deux termes que nous voulons trouver ne sont pas connus, nous pouvons utiliser la formule suivante:

Il peut vous servir: Tesseldos: caractéristique, types (réguliers, irréguliers), exemples

Propriété 3

Les nombres a_n déjà_{N + 1} ils sont  Coprimos, c'est-à-dire qu'ils sont cousins ​​les uns avec les autres, ce qui signifie qu'ils n'ont aucun facteur commun en commun.

Propriété 4

Une propriété très intéressante est celle du quotient entre les termes_2n déjà_n, qui vaut 1, quand n = 1. C'est-à-dire:

pour₂ / pour₁ = 1

Nous pouvons facilement le vérifier avec la liste des numéros de Fibonacci.

D'un autre côté, si n ≠ 1, alors le quotient est:

pour_2n / pour_n = A_n  + 2e_N-1

Par exemple, si n = 3, alors un _2n = A₆ = 8 et₃ = 2. Aussi:

8/2 = 2 + 2. pour₂ = 2 + 2. 1

En effet: 8/2 = 4 et 2 + (2.1) = 4. Il peut être vérifié que toute valeur n est respectée.

Propriété 5

Le ratio r_n = A_{N + 1} / pour_{n ,} Lorsque n devient grand, converge vers le Raison de l'or soit Proportion de l'auré, Un nombre irrationnel qui survient fréquemment dans la nature, donnée par:

Relations naturelles de la succession de Fibonacci

La succession de Fibonacci dans les plantes

Les manifestations de la succession de Fibonacci abondent dans le royaume végétal

Les branches de certains arbres sortent chaque année selon la succession de Fibonacci. La première année, le coffre se développe sans lancer de branche, après un an, il en produit un et donc à chaque année. À son tour, chaque branche peut en lancer une autre nouvelle après un an, tout comme les lapins se reproduisent.

Le centre de fleurs de tournesol contient les graines disposées en faisceaux en spirale logarithmique, dans les deux sens, dont les quantités correspondent à deux nombres de Fibonacci consécutifs.

Des chiffres de Fibonacci sont présents dans le nombre de pétales de fleurs de tournesol et de margarite, ainsi que dans de nombreux modèles dans lesquels les plantes ont leurs feuilles.

Peut vous servir: variable ordinale

Les experts disent que de cette façon les plantes optimisent l'espace pour que les feuilles et les fleurs aient une croissance optimale.

Avec un point central comme point de départ, ces structures se développent et reçoivent la lumière du soleil, donc les nouvelles feuilles et les pétales doivent couvrir le moins possible ceux qui sont sortis en premier. Et la meilleure façon d'y parvenir est d'adopter un schéma de croissance en termes de séquence Fibonacci.

La succession de Fibonacci chez les animaux

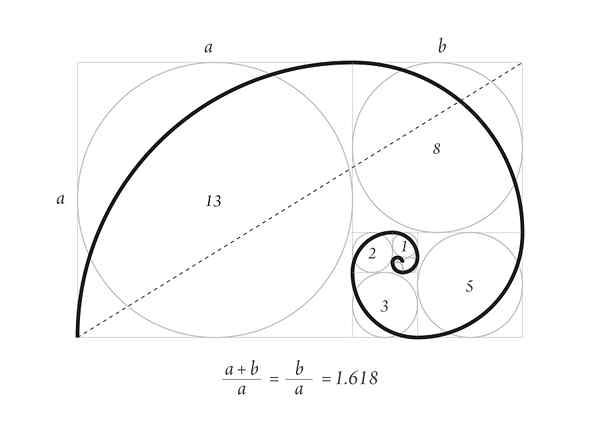La spirale de Durero avec le premier nombre de la succession de Fibonacci

La spirale durable de l'image supérieure fait partie du schéma de croissance des coquilles chez les animaux marins et les cornes de certains ruminants.

Commencez avec deux carrés 1, l'un sur l'autre, puis un carré de côté 2 à côté, qui constitue un rectangle du côté 3, dont les côtés ont la proportion d'or.

Ci-dessous se trouve un carré de côté 3 et à gauche un carré du côté 5. Au-dessus, il y a un carré de côté 8 et à droite un carré de côté 13. Ce sont les premiers nombres de la succession.

Enfin, la spirale est dessinée en touchant les points des coins des carrés, comme on le voit sur la figure.

Applications

La succession de Fibonacci est appliquée dans divers domaines:

-Dans l'art, la proportion dorée liée à la succession de Fibonacci apparaît dans les gens et les choses représentées par de grands artistes tels que Leonardo da Vinci, Miguel Ángel et Alberto Durero.

-Les proportions du partenaire à Athènes répondent également au numéro d'or.

-Dans les compositions de Mozart, Beethoven, Schubert et Debussy.

-Pour concevoir des objets dont les proportions semblent harmonieuses aux yeux humains, tels que les cartes de crédit, les conteneurs, les drapeaux.

-En bourse, il est utilisé pour prédire quels prix reviennent sa tendance.

Les références

1. Succession de Fibonacci. Récupéré de: BlogEduCastur.est.
2. Stewart, J. 2007. Précalation. 5e. Édition. Cengage Learning.
3. Vargas, m. Applications de succession de Fibonacci. Récupéré de: matesup.CL.
4. Wikipédia. Numéro de Fibonacci. Récupéré de: dans.Wikipédia.org.