Règle empirique Comment l'appliquer, à quoi sert-elle, les exercices résolus

Ongle Règle empirique C'est le résultat de l'expérience pratique et de l'observation de la vie réelle. Par exemple, vous pouvez savoir que les espèces d'oiseaux peuvent être observées à certains endroits à chaque époque de l'année et que l'observation peut être établie une «règle» qui décrit les cycles de vie de ces oiseaux.

Dans les statistiques, la règle empirique fait référence à la forme de regroupement des observations autour d'une valeur centrale, moyenne ou moyenne, en unités d'écart-type.

Supposons que vous ayez un groupe de personnes avec une hauteur moyenne de 1.62 mètres et un écart-type de 0.25 mètres, alors la règle empirique permettrait de définir, par exemple, combien de personnes seraient dans un intervalle de la moyenne plus ou moins un écart-type?

Selon la règle, 68% des données sont plus ou moins un écart-type de la moyenne, c'est-à-dire que 68% des personnes du groupe auront une hauteur entre 1.37 (1.62-0.25) et 1.87 (1.62 + 0.25) mètres.

[TOC]

D'où vient la règle empirique?

La règle empirique est une généralisation du théorème et de la distribution normale de Tchebyshev.

Théorème de Tchebyshev

Le théorème de TchebyShev dit que: pour une certaine valeur de K> 1, la probabilité qu'une variable aléatoire soit parmi les fois moins k de l'écart type, et la moyenne plus k, l'écart type est supérieur ou égal à (1 -1 / k²).

L'avantage de ce théorème est qu'il s'applique à des variables aléatoires discrètes ou continues avec toute distribution de probabilité, mais la règle définie n'est pas toujours très précise, car elle dépend de la symétrie de la distribution. Plus la distribution de la variable aléatoire est asymétrique, moins ajustée à la règle sera son comportement.

La règle empirique définie à partir de ce théorème est:

Si k = √2, il est dit que 50% des données sont dans l'intervalle: [µ - √2 s, µ + √2 s]

Si k = 2, il est dit que 75% des données sont dans l'intervalle: [µ - 2 s, µ + 2 s]

Si k = 3, il est dit que 89% des données sont dans l'intervalle: [µ - 3 s, µ + 3 s]

Distribution normale

La distribution normale, ou Gauss Bell, permet d'établir la règle empirique ou la règle 68 - 95 - 99.7.

Peut vous servir: proportion

La règle est basée sur les probabilités d'occurrence d'une variable aléatoire à des intervalles entre la moyenne moins un, deux ou trois écarts-types et la moyenne plus un, deux ou trois écarts-types.

La règle empirique définit les intervalles suivants:

68.27% des données sont dans l'intervalle: [µ - s, µ + s]

95.45% des données sont dans l'intervalle: [µ - 2s, µ + 2s]

99.73% des données sont dans l'intervalle: [µ - 3s, µ + 3s]

Dans la figure, vous pouvez voir comment ces intervalles sont présentés et la relation entre eux en augmentant la largeur de la base graphique.

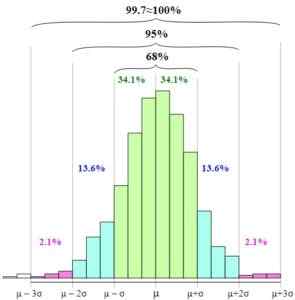Règle empirique. Melikamp [cc by-sa 4.0 (https: // CreativeCommons.org /)] La normalisation de la variable aléatoire, c'est-à-dire l'expression de la variable aléatoire en termes de variable standard ou normale, simplifie l'utilisation de la règle empirique, car la variable z a moyen égal à zéro et à l'écart type égal égal à une.

Par conséquent, l'application de la règle empirique sur l'échelle d'une variable normale standard, Z, définit les intervalles suivants:

68.27% des données sont dans l'intervalle: [-1, 1]

95.45% des données sont dans l'intervalle: [-2, 2]

99.73% des données sont dans l'intervalle: [-3, 3]

Comment appliquer la règle empirique?

La règle empirique vous permet d'abréger les calculs lorsque vous travaillez avec une distribution normale.

Supposons qu'un groupe de 100 étudiants universitaires ait un âge moyen de 23 ans, avec un écart-type de 2 ans. Quelles informations permettent la règle empirique?

L'application de la règle empirique implique de suivre les étapes:

1- Construisez les intervalles de règle

Étant donné que la moyenne est de 23 et que l'écart type est 2, les intervalles sont:

[µ - s, µ + s] = [23 - 2, 23 + 2] = [21, 25]

[µ - 2s, µ + 2s] = [23 - 2 (2), 23 + 2 (2)] = [19, 27]

[µ - 3s, µ + 3s] = [23 - 3 (2), 23 + 3 (2)] = [17, 29]

2- Calculez le nombre d'élèves dans chaque intervalle en fonction des pourcentages

(100) * 68.27% = 68 étudiants

(100) * 95.45% = environ 95 étudiants

(100) * 99.73% = 100 étudiants

3- Les intervalles d'âge sont associés aux quantités d'étudiants et interprétés

Au moins 68 étudiants ont entre 21 et 25 ans.

Peut vous servir: statistiques descriptives: historique, caractéristiques, exemples, concepts

Au moins 95 étudiants ont entre 19 et 27 ans.

Pratiquement 100 étudiants ont entre 17 et 29 ans.

Quelle est la règle empirique pour?

La règle empirique est un moyen rapide et pratique d'analyser les données statistiques, étant de plus en plus fiable dans la mesure où la distribution est proche de la symétrie.

Son utilité dépend du terrain dans lequel il est utilisé et des questions qui se posent. Il est très utile de savoir que la survenue de valeurs de trois écarts-types est presque peu probable en dessous ou au-dessus de la moyenne, même pour les variables de distribution non normales, au moins 88.8% des cas sont dans l'intervalle de trois sigma.

En sciences sociales, un résultat généralement concluant est l'intervalle de la moyenne plus ou moins deux sigma (95%), tandis qu'en physique des particules, un nouvel effet nécessite un intervalle de cinq sigmas (99.99994%) pour être considéré comme une découverte.

Exercices résolus

Lapins dans la réserve

Dans une réserve faunique, on estime qu'il y en a en moyenne 16.000 lapins avec un écart-type de 500 lapins. Si la distribution de la variable «Nombre de lapins dans la réserve» est inconnue, est-ce possible.000 et 17.000 lapins?

L'intervalle peut être présenté en ces termes:

15000 = 16000 - 1000 = 16000 - 2 (500) = µ - 2 s

17000 = 16000 + 1000 = 16000 + 2 (500) = µ + 2 s

Par conséquent: [15000, 17000] = [µ - 2 s, µ + 2 s]

En appliquant le théorème de TchebyShev, il y a une probabilité d'au moins 0.75 Que la population de lapins de la réserve faunique se situe entre 15.000 et 17.000 lapins.

Moyennes d'enfants d'un pays

Le poids moyen des enfants d'un an est normalement distribué avec une moyenne de 10 kilogrammes et un écart-type d'environ 1 kilogramme.

a) Estimer le pourcentage des enfants d'un an dans le pays qui ont un poids moyen entre 8 et 12 kilogrammes.

8 = 10 - 2 = 10 - 2 (1) = µ - 2 s

12 = 10 + 2 = 10 + 2 (1) = µ + 2 s

Par conséquent: [8, 12] = [µ - 2s, µ + 2s]

Il peut vous servir: Test de Tukey: qu'est-ce que, en cas d'exemple, un exercice résolu

Selon la règle empirique, on peut affirmer que 68.27% des enfants du pays ont entre 8 et 12 kilogrammes de poids.

b) Quelle est la probabilité de trouver un enfant d'un an de 7 kilogrammes ou moins de poids?

7 = 10 - 3 = 10 - 3 (1) = µ - 3 s

Il est connu que 7 kilogrammes de poids représente la valeur µ - 3s, ainsi que ce qu'il est connu que 99.73% des enfants ont entre 7 et 13 kilogrammes de poids. Cela ne laisse que 0.27% du total des enfants pour les extrêmes. La moitié d'entre eux, 0.135%, a 7 kilogrammes de poids ou moins et l'autre moitié, 0.135%, a 11 kilogrammes de poids ou plus.

On peut donc conclure qu'il y a une probabilité de 0.00135 qu'un enfant a 7 kilogrammes de poids ou moins.

c) Si la population du pays atteint 50 millions d'habitants et les enfants d'un an?

9 = 10 - 1 = µ - S

11 = 10 + 1 = µ + s

Par conséquent: [9, 11] = [µ - S, µ + S]

Selon la règle empirique, 68.27% des enfants d'un an sont dans l'intervalle [µ - s, µ + s]

Dans le pays, il y a 500 000 enfants d'un an (1% des 50 millions), donc 341350 enfants (68.27% de 500000) ont entre 9 et 11 kilogrammes de poids.

Les références

1. Abraira, V. (2002). Écart type et erreur standard. Magazine Semerne. Web récupéré.Archive.org.
2. Freund, R.; Wilson, W.; Mohr, D. (2010). Méthodes statistiques. Troisième Ed. Academic Press-Elsevier Inc.
3. Alicante Server (2017). Règle empirique (termes statistiques). Le glossaire a récupéré.serveur.com.
4. Lind, D.; Marchal, W.; Wathen, s. (2012). Statistiques appliquées aux entreprises et à l'économie. Dixième ed. McGraw-Hill / Inter-American du Mexique. POUR.
5. Salinas, H. (2010). Statistiques et probabilités. Récupéré de UDA.CL.
6. Sokal, R.; Rohlf, f. (2009). Introduction à la biostatistique. Deuxième ed. Dover Publications, Inc.
7. Spiegel, m. (1976). Probabilité et statistique. Série Schaum. McGraw-Hill / Inter-American du Mexique. POUR.
8. Spiegel, m.; Stephens, L. (2008). Statistiques. Quatrième Ed. McGraw-Hill / Inter-American du Mexique. POUR.
9. Revue STAT119 (2019). Questions de règle de résolution empirique. Récupéré de Stat119Review.com.
10. (2019). 68-95-99.7 Règle. Récupéré de.Wikipédia.org.